A beaker filled with water, is accelerated at a rate a ms2 in forward direction. The surface of water shall make an angle
a. tan−1(ag) backward
b. tan−1(ag) forward
c. cot−1(ga) backward
d. cot−1(ga) forward
The correct Answer is:B, D
To solve the problem of determining the angle θ that the surface of the water makes when the beaker is accelerated forward at a rate of a m/s², we can follow these steps:
Step 1: Understand the Forces Acting on the Water
When the beaker is accelerated forward, the water inside experiences a pseudo force acting in the opposite direction (backward). This is due to the acceleration of the beaker itself. The gravitational force acts downward on the water.
Step 2: Set Up the Problem
We can visualize the situation as follows:
- The beaker is accelerating to the right with acceleration a.
- The gravitational force g acts downward.
- The pseudo force acts to the left with the same magnitude as the acceleration a.
Step 3: Analyze the Resultant Forces
The surface of the water will tilt due to the balance of these forces. The angle θ that the surface makes with the horizontal can be determined by considering the forces acting on the water:
- The horizontal component of the pseudo force is a.
- The vertical component due to gravity is g.
Step 4: Use Trigonometric Relationships
From the geometry of the situation, we can relate the angle θ to the forces:
tan(θ)=OppositeAdjacent=ag
Step 5: Solve for θ
To find the angle θ, we take the arctangent of both sides:
θ=tan−1(ag)
Final Answer
Thus, the angle θ that the surface of the water makes with the horizontal is:
θ=tan−1(ag)
When the beaker is accelerated forward, the water inside experiences a pseudo force acting in the opposite direction (backward). This is due to the acceleration of the beaker itself. The gravitational force acts downward on the water.
We can visualize the situation as follows:
- The beaker is accelerating to the right with acceleration a.
- The gravitational force g acts downward.
- The pseudo force acts to the left with the same magnitude as the acceleration a.
The surface of the water will tilt due to the balance of these forces. The angle θ that the surface makes with the horizontal can be determined by considering the forces acting on the water:
- The horizontal component of the pseudo force is a.
- The vertical component due to gravity is g.
From the geometry of the situation, we can relate the angle θ to the forces:
tan(θ)=OppositeAdjacent=ag
To find the angle θ, we take the arctangent of both sides:
θ=tan−1(ag)
Thus, the angle θ that the surface of the water makes with the horizontal is:
θ=tan−1(ag)
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - D
2 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - E
8 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - B
23 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment(Section-D)
14 Videos
Similar Questions
An open rectangular tank 1.5 m wide 2m deep ad 2 m long is half filled with water. It is accelerated horizontally at 3.27m/s2 in the direction of its length determine the depth of water at each end of tank.
View SolutionA vessel contains a liquid has a constant acceleration 19.6m/s2 in horizontal direction. The free surface of water get sloped with horizontal at angle
View SolutionA closed cubical box is completely filled with water and is accelerated horizontally towards right with an acceleration a. The resultant normal force by the water on the top of the box.
View SolutionA container is filled with water , accelerating with acceleration 10m/s2 , along + ve X - axis on a smooth horizontal surface . The velocity of efflux of water at a point P t the bottom of the tank and near its left most corner is
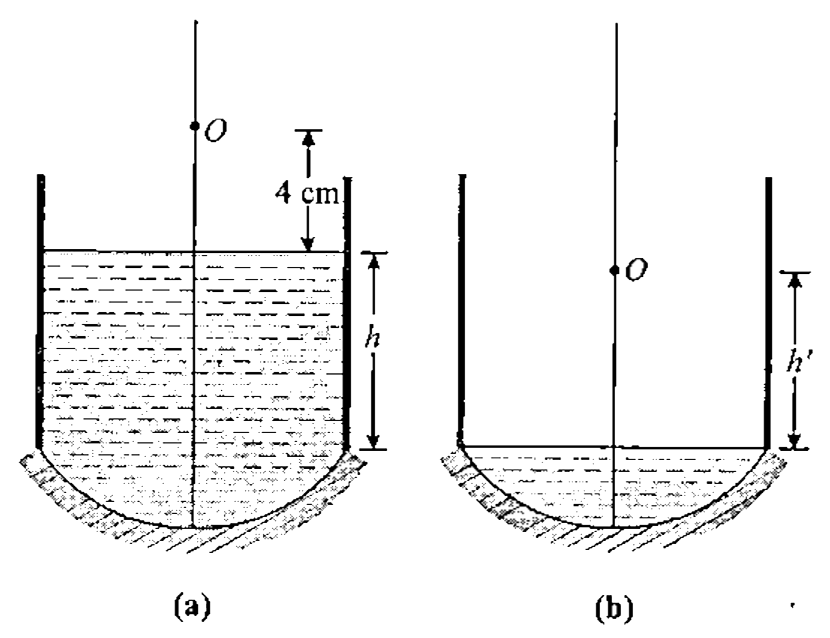
View SolutionA beaker is filled with water as shown in figure (a). The bottom surface of the beaker is a concave mirror of large radius of curvature and small aperture. The height of water is h=40cm. It is found that when an object is placed 4 cm above the water surface, the image coincides with the object. Now the water level h is reduced to zero but there will still be some water left in the concave part of the mirror as shown in figure (b). The new height of the object h' above the new water surface so that the image again coincides with the object, will be (Refractive index of water =4/3)
View SolutionA beaker is completely filled with water at 4∘C. It will overflow if
View SolutionRate of transpiration higher than rate of water absorption shall cause
View SolutionA uniform capillary tube of inner radius r is dipped vertically into a beaker filled with water. The water rises to a height h in the capillary tube above the water surface in the beaker. The surface tension of water is σ. The angle of contact between water and the wall of the capillary tube is θ. Ignore the mass of water in the meniscus. Which of the following statements is (are) true?
View SolutionA small block of wood of specific gravity 0.5 is subnerged at a depth of 1.2 m in a vessel filled with water. The vessel is accelerated upwards with an acceleration a0=g2. Time taken by the block to reach the surface, if it is released with zero initial velocity is (g=10m/s2)
View SolutionSuppose that water is emptied from a spherical tank of radius 10 cm. If the depth of the water in the tank is 4 cm and is decreasing at the rate of 2 cm/sec, then the radius of the top surface of water is decreasing at the rate of
View Solution
