A particle of mass 3 kg moves in aone dimensional field along x-axis. The force due to the field depends on its position as F=729x6−64 . Find the state equilibrium position. Determine the time period of osciallations for small amplitude osciallations about the stable equlibrium position.
To solve the problem step by step, we will follow the necessary physics principles and calculations.
Step 1: Determine the Equilibrium Position
The equilibrium position is found when the net force acting on the particle is zero. The force is given by:
F=729x6−64
To find the equilibrium position, we set the force equal to zero:
729x6−64=0
Step 2: Solve for x
Rearranging the equation gives:
729x6=64
Now, we divide both sides by 729:
x6=64729
Next, we take the sixth root of both sides:
x=(64729)16
Calculating the sixth root:
x=23
Thus, the equilibrium position is:
x=23m
Step 3: Determine the Stability of the Equilibrium Position
To check if this equilibrium position is stable, we need to find the second derivative of the potential energy (or the first derivative of the force) and evaluate it at the equilibrium position.
First, we find the derivative of the force:
F=729x6−64
Taking the derivative with respect to x:
dFdx=6×729x5=4374x5
Step 4: Evaluate the Derivative at the Equilibrium Position
Now we evaluate this derivative at x=23:
dFdx∣∣∣x=23=4374(23)5
Calculating (23)5:
(23)5=32243
Now substituting this back:
dFdx∣∣∣x=23=4374×32243
Calculating this gives a positive value, indicating that the equilibrium position is stable.
Step 5: Calculate the Time Period of Oscillation
The time period T for small oscillations can be calculated using the formula:
T=2π√mk
Where k is the force constant, which we can find by evaluating the second derivative of the force at the equilibrium position:
k=d2Fdx2
Taking the derivative again:
d2Fdx2=5×4374x4=21870x4
Now we evaluate this at x=23:
k=21870(23)4
Calculating (23)4:
(23)4=1681
So,
k=21870×1681
Calculating this gives:
k=34992081
Step 6: Substitute Values into the Time Period Formula
Now substituting m=3kg and k into the time period formula:
T=2π
⎷334992081
Calculating this gives:
T=2π√3×81349920
After simplifying, we find the final value of T.
Final Answer
The equilibrium position is x=23m and the time period of oscillations for small amplitude oscillations about this stable equilibrium position is calculated as:
T≈8√3s
The equilibrium position is found when the net force acting on the particle is zero. The force is given by:
Rearranging the equation gives:
To check if this equilibrium position is stable, we need to find the second derivative of the potential energy (or the first derivative of the force) and evaluate it at the equilibrium position.
Now we evaluate this derivative at x=23:
The time period T for small oscillations can be calculated using the formula:
Now substituting m=3kg and k into the time period formula:
⎷334992081
The equilibrium position is x=23m and the time period of oscillations for small amplitude oscillations about this stable equilibrium position is calculated as:
Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - EXAMPLE
21 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - Exercise
18 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( SECTION-I(SUBJECTIVE TYPE QUESTIONS) )
7 Videos
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
4 Videos
Similar Questions
A partical of mass m is located in a unidimensionnal potential field where potentical energy of the partical depends on the coordinates xasU(x)=Ax2−Bx where A and B are positive constant.
Find the time period of small oscillation that the partical perform about equilibrium possition.
View SolutionA partical of mass m is located in a unidimensionnal potential field where potentical energy of the partical depends on the coordinates xas:U(x)=U0(1−cosAx),U0 and A constants.
Find the period of small oscillation that the partical performs about the equilibrium position.
View SolutionA particle of mass 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is

View SolutionA particle of mass 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is

View SolutionA particle of mass 1 kg is moving along x - axis and a force F is also acting along x -axis in such a way that its displacement is varying as : x=3t2. Find work done by force F when it will move 2m.
View SolutionForce acting on a particle constrained to move along x-axis is F=(x−4). Here, F is in newton and x in metre. Find the equilibrium position and state whether it is stable or unstable equilibrium.
View SolutionA particle moving with S.H.M. has velocitiesof 4cm/s and 3cm/s at distances of 3 cm and 4 cm respectively from the equilibrium position. Find
(a)The amplitude of the osciallation
(b) Time period
(c ) The velocity of the particle as is pases through the equilibrium position.
View SolutionA particle is moving along x-axis under the action of force, F which varies with its position as F∝14√x. Find the variation of power due to this fore with x.
View SolutionThe potential energy U(x) of a particle moving along x - axis is given by U(x)=ax−bx2. Find the equilibrium position of particle.
View SolutionA particle of mass 4kg moves simple harmonically such that its PE (U) varies with position x, as shown. The period of oscillations is :-
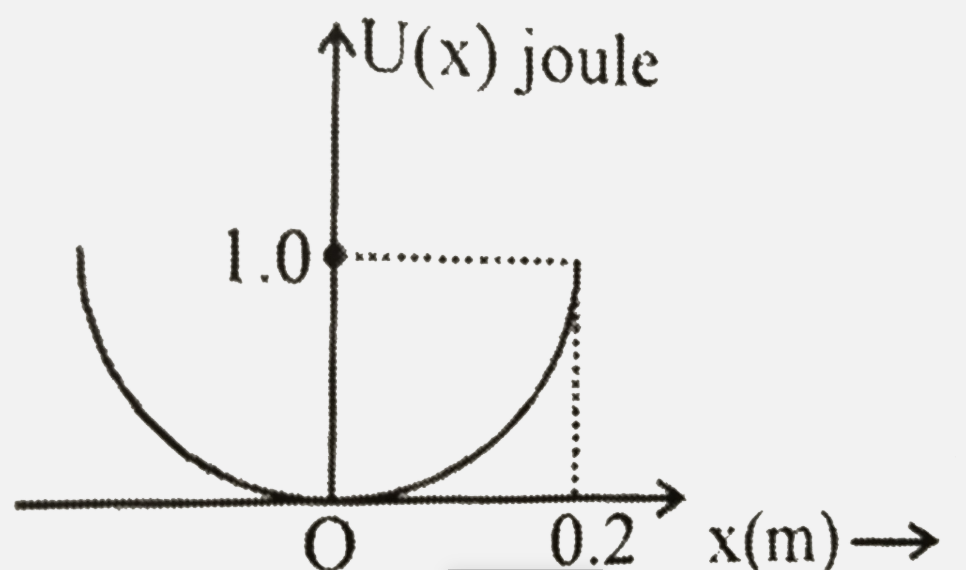
View Solution