An isotropic point source kept at 'O' produces intensity l0 at point A. find the mean energy flow rate through a ring centred at A and having its plane perpendicular to the line OA. The distance OA is x arid radius of ring is R.
To solve the problem, we need to find the mean energy flow rate through a ring centered at point A, which is at a distance x from the isotropic point source at point O. The radius of the ring is R.
1. Understanding Intensity:
The intensity I0 at point A is defined as the power per unit area received from the isotropic point source. For a point source, the intensity decreases with the square of the distance from the source.
2. Area of the Sphere:
The intensity I0 at point A can be expressed in terms of the power P emitted by the source and the area of a sphere with radius x:
I0=P4πx2
3. Finding the Radius of the Ring:
The radius of the ring is R. The distance from the source O to the ring's center A is x. The distance from the source O to any point on the ring can be calculated using the Pythagorean theorem:
r′=√x2+R2
4. Intensity at the Ring:
The intensity I′ at the ring can be expressed as:
I′=P4πr′2=P4π(x2+R2)
5. Area of the Ring:
The area A of the ring can be calculated using the circumference of the ring multiplied by an infinitesimal width dθ:
A=2πR⋅dθ
However, we need to consider the solid angle subtended by the ring at point A.
6. Solid Angle:
The solid angle Ω subtended by the ring can be calculated as:
Ω=2π(1−cosθ)
where cosθ=xr′.
7. Mean Energy Flow Rate:
The mean energy flow rate through the ring can be expressed as:
E=I′⋅A
Substituting the expressions for I′ and A:
E=P4π(x2+R2)⋅(2πR⋅dθ)
8. Final Expression:
After simplifying, we find:
E=PR2(x2+R2)
Final Answer:
The mean energy flow rate through the ring is:
E=PR2(x2+R2)
The intensity I0 at point A is defined as the power per unit area received from the isotropic point source. For a point source, the intensity decreases with the square of the distance from the source.
The intensity I0 at point A can be expressed in terms of the power P emitted by the source and the area of a sphere with radius x:
I0=P4πx2
The radius of the ring is R. The distance from the source O to the ring's center A is x. The distance from the source O to any point on the ring can be calculated using the Pythagorean theorem:
r′=√x2+R2
The intensity I′ at the ring can be expressed as:
I′=P4πr′2=P4π(x2+R2)
The area A of the ring can be calculated using the circumference of the ring multiplied by an infinitesimal width dθ:
A=2πR⋅dθ
However, we need to consider the solid angle subtended by the ring at point A.
The solid angle Ω subtended by the ring can be calculated as:
Ω=2π(1−cosθ)
where cosθ=xr′.
The mean energy flow rate through the ring can be expressed as:
E=I′⋅A
Substituting the expressions for I′ and A:
E=P4π(x2+R2)⋅(2πR⋅dθ)
After simplifying, we find:
E=PR2(x2+R2)
The mean energy flow rate through the ring is:
E=PR2(x2+R2)
Topper's Solved these Questions
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - Assignment (Section-J) (Paragraph Type Questions)
4 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - EXERCISE
20 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - Assignment (Section-I) (Subjective Type Questions)
8 Videos
- WAVE OPTICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assignment (Section-J (Aakash Challengers question))
1 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - D)
13 Videos
Similar Questions
Find the radius of gyration of a circular ring of radius r about a line perpendicular to the plane of the ring and passing through one of this particles.
View SolutionThere is a conducting ring of radius R. Another ring having current i and radius r(r<<R) is kept on the axis of bigger ring such that its center lies on the axis of bigger ring at a distance x from the center of bigger ring and its plane is perpendicular to that axis. The mutual inductance of the bigger ring due to the smaller ring is
View SolutionFind the intensity of gravitational field at a point lying at a distance x from the centre on the axis of a ring of radius a and mass M.
View SolutionIf plane passes through the point (1, 1,1) and is perpendicular to the line,x−13=y−10=z−14, then its perpendicular distance from the origin is
View SolutionIf plane passes through the point (1, 1,1) and is perpendicular to the line,x−13=y−10=z−14, then its perpendicular distance from the origin is
View SolutionTwo rings of same radius and mass are placed such that their centres are at a common point and their planes are perpendicular to each other. The moment of inertia of the system about an axis passing through the centre and perpendicular to the plane of one of the rings is (mass the ring =m, radius=r)
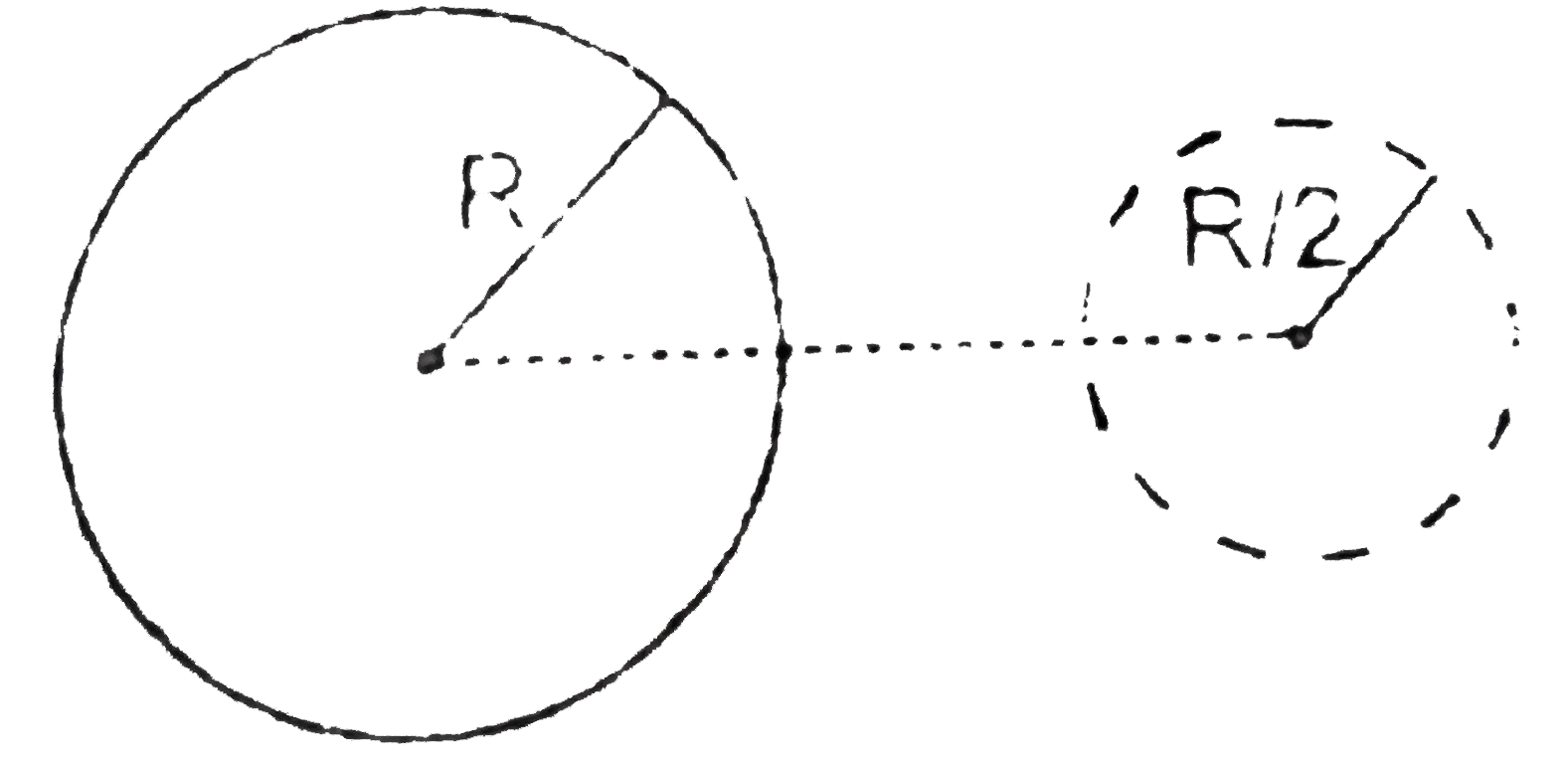
View SolutionA ring of radius R having a linear charge density λ moves towards a solid imaginary sphere of radius R2, so that the centre of ring passes through the centre of sphere. The axis of the ring is perpendicular to the line joining the centres of the ring and the sphere. The maximum flux through the sphere in this process is
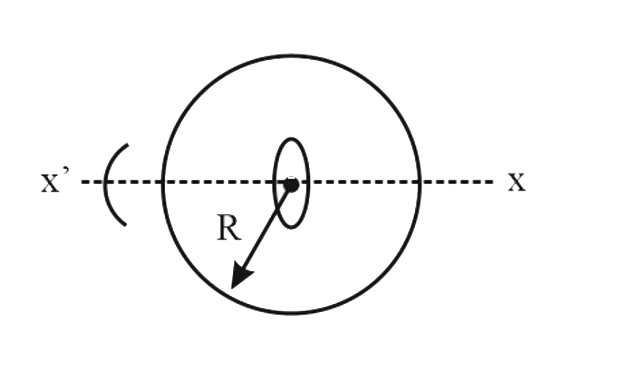
View SolutionA non-conducting ring of radius R having uniformly distributed charge Q starts rotating about x-x' axis passing through diameter with an angular acceleration α, as shown in the figure. Another small conducting ring having radius a(a<<R) is kept fixed at the centre of bigger ring is such a way that axis xx' is passing through its centre and perpendicular to its plane. If the resistance of small ring is r=1Ω , find the induced current in it in ampere.
(Given q=16×102μ0C,R=1m,a=0.1m,α=8rad s−2
View SolutionA uniformly charged disc of radius R with a total charge Q lies in the XY -plane. Find the electric field at a point at a point P, along the Z-a xis that passes through the centre of the discc perpendicular to its plane. Discuss the limit when R>>z.
Strategy : By treating the disc as a set of concentric uniformly charged rings, the problem could be solved by using the result obtained in example for ring. Consider a ring of radius of radius r' and thickness as shown in figure.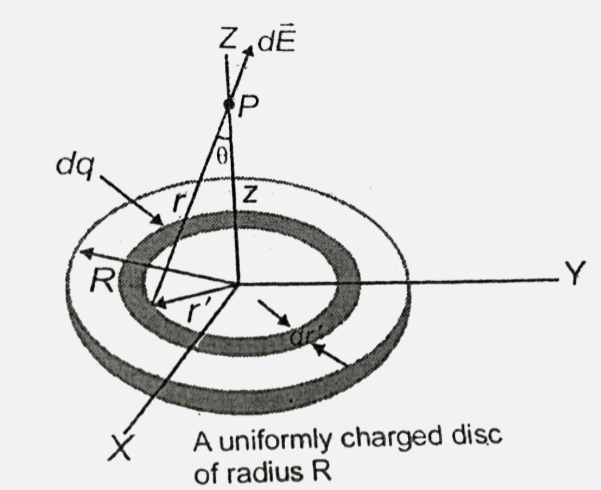
View SolutionA ring of mass m and radius r rotates about an axis passing through its centre and perpendicular to its plane with angular velocity ω. Its kinetic energy is
View Solution
