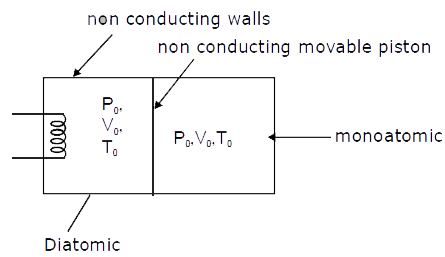
A cylinderical vessel made of thermally isulating material is divided into two equal parts by an insulating (moveable & smooth) piston. Both parts hae same ideal gas (VpCv=32). The gas in left part is supplied heat such that volume of right part becomes one fourth of initial value.
(PVT,PVT)
(1) In right part, the pressure becomes eight times of its inital value
(2) In right part, the temperature becomes two times
(3) In right part, work done by gas =3PV
(4) In right part, work done by gas=-2PV
The correct Answer is:1,2,4
To solve the problem step by step, we will analyze the situation involving the ideal gas in the cylindrical vessel divided by a piston.
Step 1: Understand the initial conditions
- We have a cylindrical vessel divided into two equal parts by a movable piston.
- The gas in both parts is an ideal gas with the ratio VpCv=32.
- Let the initial pressure and volume in both parts be P0 and V0 respectively.
Hint: Identify the initial state of the gas and the properties of the ideal gas.
Step 2: Analyze the changes in the right part
- The volume of the right part becomes one-fourth of its initial value, so the new volume V2=V04.
- Since the vessel is thermally insulating, the process in the right part is adiabatic.
Hint: Recognize that an adiabatic process means no heat exchange occurs.
Step 3: Apply the adiabatic condition
- For an adiabatic process, we can use the relation:
P1Vγ1=P2Vγ2
where γ=CpCv=53 (since VpCv=32 implies Cv=32R and Cp=52R).
- Plugging in the values:
P0V530=P2(V04)53
Hint: Use the adiabatic condition to relate the pressures and volumes before and after the change.
Step 4: Solve for the new pressure P2
- Rearranging gives:
P2=P0⎛⎜⎝V0V04⎞⎟⎠53=P0(4)53=P0⋅453=P0⋅8
- Thus, P2=8P0.
Hint: Calculate the new pressure using the derived relationship.
Step 5: Calculate the new temperature T2
- The temperature can be calculated using the ideal gas law:
T=PVnR
- Initial temperature T1=P0V0nR and final temperature:
T2=P2V2nR=8P0⋅V04nR=2⋅P0V0nR=2T1
Hint: Use the ideal gas law to find the relationship between pressure, volume, and temperature.
Step 6: Calculate the work done in the right part
- The work done in an adiabatic process can be calculated using:
W=P2V2−P1V1γ−1
- Substituting the values:
W=8P0⋅V04−P0V053−1=2P0V0−P0V023=P0V023=−2P0V0
Hint: Use the work formula for adiabatic processes to find the work done.
Conclusion
Based on the calculations:
1. The pressure in the right part becomes 8P0 (Option 1 is correct).
2. The temperature in the right part becomes 2T1 (Option 2 is correct).
3. The work done by the gas is −2PV (Option 4 is correct).
Thus, the correct options are 1, 2, and 4.
- We have a cylindrical vessel divided into two equal parts by a movable piston.
- The gas in both parts is an ideal gas with the ratio VpCv=32.
- Let the initial pressure and volume in both parts be P0 and V0 respectively.
- The volume of the right part becomes one-fourth of its initial value, so the new volume V2=V04.
- Since the vessel is thermally insulating, the process in the right part is adiabatic.
- For an adiabatic process, we can use the relation:
P1Vγ1=P2Vγ2
where γ=CpCv=53 (since VpCv=32 implies Cv=32R and Cp=52R).
P0V530=P2(V04)53
- Rearranging gives:
P2=P0⎛⎜⎝V0V04⎞⎟⎠53=P0(4)53=P0⋅453=P0⋅8
- Thus, P2=8P0.
- The temperature can be calculated using the ideal gas law:
T=PVnR
- Initial temperature T1=P0V0nR and final temperature:
T2=P2V2nR=8P0⋅V04nR=2⋅P0V0nR=2T1
- The work done in an adiabatic process can be calculated using:
W=P2V2−P1V1γ−1
- Substituting the values:
W=8P0⋅V04−P0V053−1=2P0V0−P0V023=P0V023=−2P0V0
Based on the calculations:
1. The pressure in the right part becomes 8P0 (Option 1 is correct).
2. The temperature in the right part becomes 2T1 (Option 2 is correct).
3. The work done by the gas is −2PV (Option 4 is correct).
Topper's Solved these Questions
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - TRY YOURSELF
12 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - EXERCISE
20 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Assignment (Section-I) Subjective Type
5 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assignment (Section-J) Akash Challengers Questions
7 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
Similar Questions
What is the essential condition for thermodynamic equilibrium?
View SolutionWhen are the two bodies in thermal equilibrium?
View SolutionTwo moles of an ideal gas are contained in a vertical cylinder with a frictionless piston. The piston is slowly displaced so that expansionin gas is isothermal at temperature T0=400K. find the amount of work done in increasing the volume to 3 times.t ake atmospheric pressure =105N/m2
View SolutionA slab of cunductivity k is in the shape of trapezoid as shown I figure. If the two end faces be maintained at temperature T1=50∘CandT2=25∘C, then determine the thermal current through the slab by ignoring any heat loss through the lateral surfaces.
 .
.
View SolutionA : PARSEC and light year, both measure time
R : Both have dimension of time.
View SolutionAn adiabatic vessel of total volume V is divided into two equal parts by a conducting separtor. The is fixed in this position. The part on the left contains one mole of an ideal gas (U=1.5nRT) and the part on the right contains two moles of the same gas. initially, the pressure on each side is p. the system is left for sufficiant time so that a steady state is reached. find (a) the work done by the gas in the left part during the process, (b) the temperature on the two sides in the beginning, (c ) the final common temperature reached by the gases, (d) the heat given to the gas in the right part and (e) the increase in the internal energy of the gas in the left part.
View SolutionAn insulting container of volume 2V_(0) is divided in two equal parts by a diathermic (conducting) fixed piston. The left part contains one mole of monoatomic ideal gas whereas right part contains two moles of the same gas. Initial pressue on each side is P_(0) . The system is left for sufficient time so that a steady state is reached. Find (a) the work done by the gas in the left part during the process, (b) initial temperature in the two sides, (c) the final common temperature reached by the gases, (d) the heat given to the gas in the right part and (e) the increase in the internal energy of the gas in the left part.
View SolutionA thermally insulated vessel is divided in to two parts by a heat insulating piston which can move in the vessel without the friction. The left part of the vessel contains one mole of an ideal monatomic gas, & the right part is empty. The piston is connected to the right wall of the vessel through a spring whose length in free state is equal to the length of the vessel as shown in the figure. Determine the heat capacity C of the system, neglecting the heat capacity of the vessel, piston and spring.

View SolutionFollowing figure shows on adiabatic cylindrical container of volume V0 divided by an adiabatic smooth piston (area of cross-section = A ) in two equal parts. An ideal gas (Cp/Cy=λ) is at pressure P and temperature T in left part and gas at pressure P and temperature T in right part. The piston is slowly displaced and released at a position where it can stay in equilibrium. The final pressure of the two parts will be (Suppose x = displacement of the piston)

View SolutionA cylinderical vessel made of thermally isulating material is divided into two equal parts by an insulating (moveable & smooth) piston. Both parts hae same ideal gas ((V_(p))/(C_(v))=(3)/(2)) . The gas in left part is supplied heat such that volume of right part becomes one fourth of initial value. (PVT,PVT) (1) In right part, the pressure becomes eight times of its inital value (2) In right part, the temperature becomes two times (3) In right part, work done by gas =3PV (4) In right part, work done by gas=-2PV
View SolutionA cylindrical container having nonconducting walls is partitioned in two equal parts such that the volume of the each parts is equal toV0. A movable nonconducting piston is kept between the two parts. Gas on left is slowly heated so that the gas on right is compressed upto volume V08. Find pressure and temperature on both sides if initial pressure and temperature, were P0andT0 respectively. Also find heat given by the heater to the gas. (number of moles in each part is n)
View Solutionएक पिस्टन किसी गैस सिलिंडर को दो भागो में विभाजित करता है | प्रारंभ में पिस्टन को ऐसे दबाते है जिससे एक भाग में दाब P तथा आयतन 5V है और दूसरे भाग में 8P दाब तथा आयतन V है | अब पिस्टन को स्वतंत्र छोड़ दिया जाता है , रुद्धोष्म तथा समतापी प्रक्रमों के लिए नये दाब तथा आयतन की गणना कीजिये ( गैस के लिए γ=1.5 )
View SolutionA cylindrical vessel made of thermally insulating material is divided into two equal parts by an insulating and. Movable piston. Both parts contain ideal monoatomic gas . The gas in the left part is supplied heat such that the volume of right part becomes one-eight of its initial volume . Work done by the gas in the right part is
View SolutionA thermally insulated container is divided into two parts by a screen. In one part the pressure and temperature are P and T for an ideal gas filled. In the second part it is vacuum. If now a small hole is created in the screen, then the temperature of the gas will
View SolutionAn adiabatic vessel of total volume V is divided into two equal parts by a conducting separator. The separator is fixed in this position. The part on the left contains one mole of an ideal gas (U=1.5nRT) and the part on the right contains two moles of the same gas. initially, the pressure on each side is p. the system is left for sufficient time so that a steady state is reached. find (a) the work done by the gas in the left part during the process, (b) the temperature on the two sides in the beginning, (c ) the final common temperature reached by the gases, (d) the heat given to the gas in the right part and (e) the increase in the internal energy of the gas in the left part.
View Solution
