A polyatomic ideal gas with linear structure is being supplied that Q in a polytropic process. The work done upon gas is QN. The molar specific heat of the gas for the process is N'NR2[N+1]. Then find the value of N' (here N is a constant).
The correct Answer is:5
To solve the problem step by step, we will use the first law of thermodynamics and the properties of a polyatomic ideal gas.
Step 1: Apply the First Law of Thermodynamics
The first law of thermodynamics states that:
ΔQ=ΔU+ΔW
Where:
- ΔQ is the heat added to the system,
- ΔU is the change in internal energy,
- ΔW is the work done by the system.
In this case, we are given:
- ΔQ=Q
- The work done on the gas is given as ΔW=−QN (since work done on the gas is negative).
Thus, we can write:
Q=ΔU−QN
Step 2: Rearranging the Equation
Rearranging the equation gives:
Q+QN=ΔU
Factoring out Q:
Q(1+1N)=ΔU
Step 3: Expressing Change in Internal Energy
For a polyatomic ideal gas with linear structure, the degrees of freedom F is given by:
F=5(3 translational + 2 rotational)
The change in internal energy ΔU can be expressed as:
ΔU=F2RT
Substituting F=5:
ΔU=52RT
Step 4: Equating the Two Expressions for ΔU
From Step 2, we have:
Q(1+1N)=52RT
Now, we can express QT:
QT=5R2⋅11+1N=5RN2(N+1)
Step 5: Relating to Molar Specific Heat
The molar specific heat for the process is given as:
C=N′NR2(N+1)
Setting the two expressions for QT equal to each other:
5RN2(N+1)=N′NR2(N+1)
Step 6: Canceling Common Terms
Since R and 12(N+1) are common on both sides, we can cancel them:
5N=N′
Step 7: Final Result
Thus, we find:
N′=5
Conclusion
The value of N′ is 5.
---
The first law of thermodynamics states that:
ΔQ=ΔU+ΔW
Where:
- ΔQ is the heat added to the system,
- ΔU is the change in internal energy,
- ΔW is the work done by the system.
- ΔQ=Q
- The work done on the gas is given as ΔW=−QN (since work done on the gas is negative).
Q=ΔU−QN
Rearranging the equation gives:
Q+QN=ΔU
Factoring out Q:
Q(1+1N)=ΔU
For a polyatomic ideal gas with linear structure, the degrees of freedom F is given by:
F=5(3 translational + 2 rotational)
The change in internal energy ΔU can be expressed as:
ΔU=F2RT
Substituting F=5:
ΔU=52RT
From Step 2, we have:
Q(1+1N)=52RT
Now, we can express QT:
QT=5R2⋅11+1N=5RN2(N+1)
The molar specific heat for the process is given as:
C=N′NR2(N+1)
Setting the two expressions for QT equal to each other:
5RN2(N+1)=N′NR2(N+1)
Since R and 12(N+1) are common on both sides, we can cancel them:
5N=N′
Thus, we find:
N′=5
The value of N′ is 5.
Topper's Solved these Questions
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - TRY YOURSELF
12 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - EXERCISE
20 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Assignment (Section-I) Subjective Type
5 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assignment (Section-J) Akash Challengers Questions
7 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
Similar Questions
an ideal diatomic gas undergoes a polytropic process described by the equation P√V=constant . The molar heat capacity of the gas during this process is
View SolutionA certain amount of ideal monoatomic gas undergoes a process given by TV1/2= constant. The molar specific heat of the gas for the process will be given by
View SolutionFigure demonstrates a polytropic process (i.e.PVn = constant ) for an ideal gas. The work done by the gas be in the process AB is
_S01_086_Q01.png)
View SolutionIn a thermodynamic process on an ideal diatomic gas, work done by the gas is η times the heat supplied (η<1). The molar heat capacity of the gas for the process is
View SolutionFind the molar specific heat of the process p=aT for a monoatomic gas, a being constant.
View SolutionAn ideal diatomic gas is expanded so that the amount of heat transferred to the gas is equal to the decrease in its internal energy.
The molar specific heat of the gas in this process is given by C whose value is
View SolutionIf the molar specific heat at constant pressure for a polyatomic non-linear gas is x and the molar specific heat at constant volume for a diatomic gas is y, find the value of x/y.
View SolutionIn isobaric process of ideal gas (f=5) work done by gas is equal of 10J. Then heat given to gas during process:
View SolutionThe state of an ideal gas changed as shown, at constant temperature T0 If heat supplied to the gas in process B→C is thrice of work done by gas in A→B , then the pressure of gas in state C is P02n . Find the value of n.
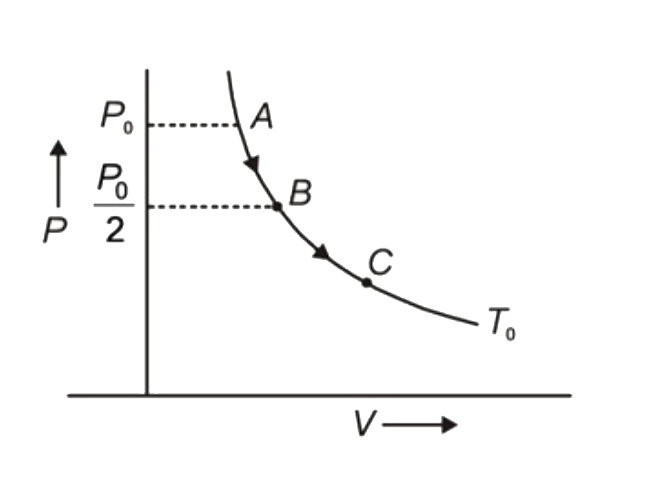
View Solutionn' moles of an ideal gas undergoes a process A→B as shown in the figure. The maximum temperature of the gas during the process will be:
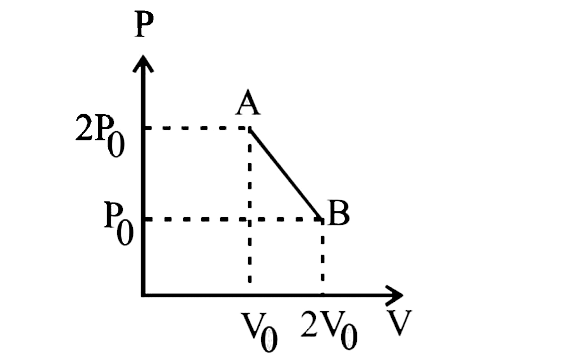
View Solution
