The energies of three conservative energy levels L3,L2 and L1 of hydrogen atom are E0. 4E09 and E04 respectively. A photon of wavelength λ is emitted for a transition L3 to L1 .What will be the wavelength of emission for transition L2 to L1 ?
16λ31
27λ7
1920λ
λ
The correct Answer is:B
To solve the problem, we need to find the wavelength of emission for the transition from energy level L2 to L1 in a hydrogen atom, given the energies of the levels and the wavelength for the transition from L3 to L1.
1. Identify the Energy Levels:
- Given:
- Energy of L3=E0
- Energy of L2=4E09
- Energy of L1=E04
2. Calculate the Energy Difference for Transition L3 to L1:
- The energy difference ΔE31 for the transition from L3 to L1 is:
ΔE31=EL3−EL1=E0−E04=4E04−E04=3E04
3. Relate Energy Difference to Wavelength:
- The energy of the emitted photon is related to its wavelength λ by the equation:
E=hcλ
- For the transition L3 to L1:
hcλ=3E04
- Rearranging gives:
hc=3E0λ4
4. Calculate the Energy Difference for Transition L2 to L1:
- The energy difference ΔE21 for the transition from L2 to L1 is:
ΔE21=EL2−EL1=4E09−E04
- To subtract these fractions, we need a common denominator. The least common multiple of 9 and 4 is 36:
ΔE21=(4E0⋅436)−(E0⋅936)=16E036−9E036=7E036
5. Relate Energy Difference to Wavelength for Transition L2 to L1:
- Using the energy-wavelength relationship for this transition:
hcλ′=7E036
- Rearranging gives:
hc=7E0λ′36
6. Equate the Two Expressions for hc:
- From the two expressions for hc:
3E0λ4=7E0λ′36
- Cancel E0 from both sides:
3λ4=7λ′36
7. Solve for λ′:
- Cross-multiplying gives:
3⋅36λ′=7⋅4λ
108λ′=28λ
λ′=28λ108=7λ27
Final Answer:
The wavelength of emission for the transition from L2 to L1 is:
λ′=727λ
- Given:
- Energy of L3=E0
- Energy of L2=4E09
- Energy of L1=E04
- The energy difference ΔE31 for the transition from L3 to L1 is:
ΔE31=EL3−EL1=E0−E04=4E04−E04=3E04
- The energy of the emitted photon is related to its wavelength λ by the equation:
E=hcλ
- For the transition L3 to L1:
hcλ=3E04
- Rearranging gives:
hc=3E0λ4
- The energy difference ΔE21 for the transition from L2 to L1 is:
ΔE21=EL2−EL1=4E09−E04
- To subtract these fractions, we need a common denominator. The least common multiple of 9 and 4 is 36:
ΔE21=(4E0⋅436)−(E0⋅936)=16E036−9E036=7E036
- Using the energy-wavelength relationship for this transition:
hcλ′=7E036
- Rearranging gives:
hc=7E0λ′36
- From the two expressions for hc:
3E0λ4=7E0λ′36
- Cancel E0 from both sides:
3λ4=7λ′36
- Cross-multiplying gives:
3⋅36λ′=7⋅4λ
108λ′=28λ
λ′=28λ108=7λ27
The wavelength of emission for the transition from L2 to L1 is:
λ′=727λ
Topper's Solved these Questions
- ATOMSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ATOMSEXERCISE - ASSIGNMENT SECTION B Objective (One option is correct )
12 Videos
- ATOMSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ATOMSEXERCISE - ASSIGNMENT SECTION C Objective (More than one option is correct )
6 Videos
- ATOMSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ATOMSEXERCISE - Try Yourself
24 Videos
- ALTERNATING CURRENT BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - Assignment (Section-J) (Aakash Chailengers Questions)
2 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COMMUNICATION SYSTEMS EXERCISE - ASSIGNMENT SECTION D (Assertion-Reason)
10 Videos
Similar Questions
The energy of a I,II and III energy levels of a certain atom are E,4E3 and 2E respectively. A photon of wavelength λ is emitted during a transition from III to I. what will be the wavelength of emission for II to I?
View SolutionThe following diagram indicates the energy levels of a certain atom when the system moves from 4E level to E. A photon of wavelength λ1 is emitted. The wavelength of photon produced during its transition from 73E level to E is λ2. the ratio λ1λ2 will be
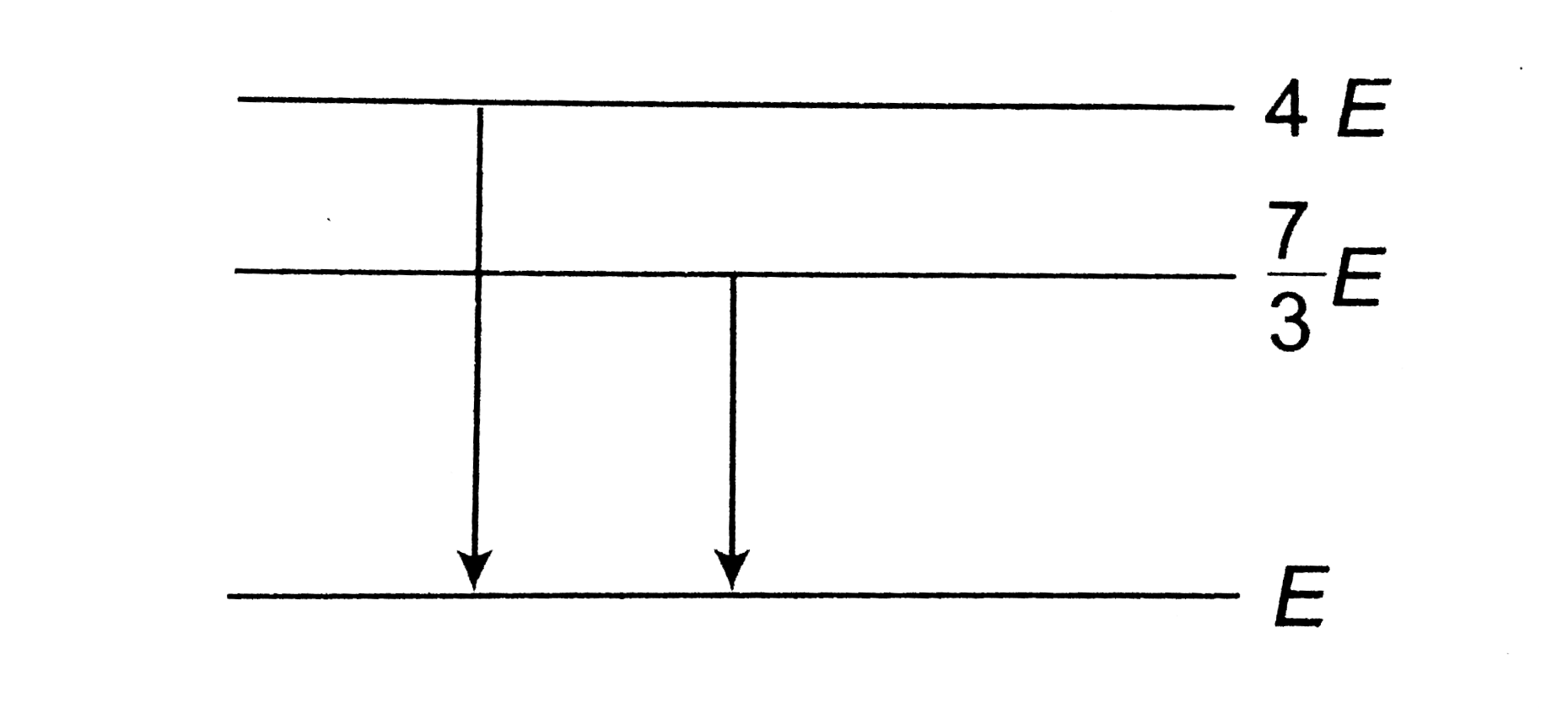
View SolutionThe following diagram indicates the energy levels of a certain atom when the system moves from 4E level to E. A photon of wavelength λ1 is emitted. The wavelength of photon produced during its transition from 73E level to E is λ2. the ratio λ1λ2 will be

View SolutionThe follwing diagram indicates the energy levels of a certain atom when the system moves from 2E level to E, a photon of wavelength λ is emitted. The wavelength of photon produced during its transition from 4E3 level to E is

View SolutionAn atom emits a spectral line of wavelength λ when an electron makes a transition between levels of energy E1andE2. Which expression correctly relates λE1andE2 ?
View SolutionConsider three converging lenses L1,L2andL3 having identical geometrical construction. The index of refraction of L1andL2areμ1andμ2 respectively. The upper half of the lens L3 has a refractive index μ1 and the lower half has μ2. A point object O is imaged at O1 by the lens L1andatO2 by the lens L2 placed in same position . If L3 is placed at the same place.

View SolutionWhen a string is divided into three segments of length l1,l2 and l3 the fundamental frequencies of these three segments are f1,f2 and f3 respectively. The original fundamental frequency f of the string is
View Solutionl1andl2 are the side lengths of two variable squares S1,andS2, respectively. If l1=l2+l32+6 then rate of change of the area of S2, with respect to rate of change of the area of S1 when l2=1 is equal to
View SolutionThe energy of a photon is equal to the kinetic energy of a
proton. The energy of the photon is E. Let λ1be the de-Broglie wavelength of the
proton and λ2 be the wavelength of the photon. The ratio λ1λ2 is proportional to
(a)E0 (b) E1/2 (c ) E−1 (d)E−2
View SolutionTwo bodies with moment of inertia l1 and l2 (l1>l2) have equal angular momentum. If E1 and E2 are the rotational kinetic energies, then
View Solution
