A line passes through The number of points with integral co-ordinates on the line strictly between A and B is
7
8
9
10
The correct Answer is:A
To find the number of points with integral coordinates on the line segment strictly between the points A(1, 1) and B(100, 1000), we can follow these steps:
Step 1: Determine the slope of the line
The slope m of the line passing through points A and B is given by the formula:
m=y2−y1x2−x1
Substituting the coordinates of points A(1, 1) and B(100, 1000):
m=1000−1100−1=99999=11
Hint: The slope indicates how steep the line is and helps in finding the equation of the line.
Step 2: Write the equation of the line
Using the point-slope form of the equation of a line, we can write:
y−y1=m(x−x1)
Substituting m=11 and point A(1, 1):
y−1=11(x−1)
Simplifying this, we get:
y=11x−10
Hint: The equation of the line helps us determine the coordinates of points on the line.
Step 3: Identify the integral points between A and B
To find the integral points strictly between A and B, we need to find integer values of x such that 1<x<100. The corresponding y values will also be integers.
From the equation y=11x−10, we can find the integral points:
1. For x=2, y=11(2)−10=12
2. For x=3, y=11(3)−10=23
3. Continuing this way, we find the values of y for x=4,5,…,99.
Hint: The equation allows us to calculate y for each integer x.
Step 4: Count the integral points
The values of x that yield integral points must be of the form:
x=11k+1
for integers k. The maximum value of x is 99, so we need to solve:
1<11k+1<100
This simplifies to:
0<11k<99⟹0<k<9
Thus, k can take values from 0 to 8, giving us 9 possible values of k.
Hint: Counting the values of k helps us find the total number of integral points.
Conclusion
The total number of integral points with coordinates on the line segment strictly between A(1, 1) and B(100, 1000) is:
8 (from k=1 to k=8)
Thus, the answer is 8.
The slope m of the line passing through points A and B is given by the formula:
m=y2−y1x2−x1
Substituting the coordinates of points A(1, 1) and B(100, 1000):
m=1000−1100−1=99999=11
Using the point-slope form of the equation of a line, we can write:
y−y1=m(x−x1)
Substituting m=11 and point A(1, 1):
y−1=11(x−1)
Simplifying this, we get:
y=11x−10
To find the integral points strictly between A and B, we need to find integer values of x such that 1<x<100. The corresponding y values will also be integers.
1. For x=2, y=11(2)−10=12
2. For x=3, y=11(3)−10=23
3. Continuing this way, we find the values of y for x=4,5,…,99.
The values of x that yield integral points must be of the form:
x=11k+1
for integers k. The maximum value of x is 99, so we need to solve:
1<11k+1<100
This simplifies to:
0<11k<99⟹0<k<9
Thus, k can take values from 0 to 8, giving us 9 possible values of k.
The total number of integral points with coordinates on the line segment strictly between A(1, 1) and B(100, 1000) is:
8 (from k=1 to k=8)
Topper's Solved these Questions
- STRAIGHT LINESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - SECTION-I (SUBJECTIVE TYPE QUESTIONS)
5 Videos
- STATISTICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - STATISTICSEXERCISE - Section-C Assertion-Reason
15 Videos
- THREE DIMENSIONAL GEOMETRY BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - ASSIGNMENT SECTION - J
10 Videos
Similar Questions
A line passes through two points A(2,−3,−1) and B(8,−1,2). The coordinates of a point on this lie at distance of 14 units from a are
View SolutionA straight line passes through the points (a, 0) and (0, b). The length of the line segment contained between the axes is 13 and the product of their intercepts on the axes is 60. Calculate the values of a and b and find the equation of the straight line.
View Solution
Knowledge Check
Of a line passes through the points (5, 3) and (8, -1), at what point will this line intersect the y - axis ?
A(0,8.33)B(0,8.67)C(0,9.00)D(0,9.67)
A straight line passes through the points P(-1, 4) and Q(5,-2). It intersects the co-ordinate axes at points A and B. M is the midpoint of the segment AB. Find :
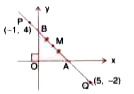
The co-ordinates of A and B.
View SolutionA straight line passes through the points P(-1, 4) and Q(5,-2). It intersects the co-ordinate axes at points A and B. M is the midpoint of the segment AB. Find :
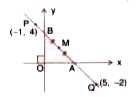
The co-ordinates of M.
View SolutionA straight line passes through the points P(-1, 4) and Q(5,-2). It intersects the co-ordinate axes at points A and B. M is the midpoint of the segment AB. Find :

The equation of the line.
View SolutionA straight line passes through the points A(-5, 2) and B(3,-6). It intersects the co-ordinate axes at points C and D . Find :
the equation of AB.
View SolutionA straight line passes through the points A(-5, 2) and B(3,6). It intersects the co-ordinate axes at points C and D . M is a point on AB which divides CD in the ratio 1: 2. Find :
the co-ordinates of point M.
View SolutionA straight line passes through the points A(-5, 2) and B(3,6). It intersects the co-ordinate axes at points C and D . M is a point on AB which divides CD in the ratio 1: 2. Find :
the co-ordinates of points C and D.
View Solutionfind the equation of the straight line which passes through the point (3,2) and whose gradient is 34.find the co-ordinate of the points on the line that are 5 units away from the point (3,2).
View Solution
