A particle is projected from the bottom of an inclined plane of inclination 30∘. At what angle α (from the horizontal) should the particle be projected to get the maximum range on the inclined plane.
30∘
45∘
15∘
75∘
The correct Answer is:A
Step by step video & image solution for A particle is projected from the bottom of an inclined plane of inclination 30^@. At what angle alpha (from the horizontal) should the particle be projected to get the maximum range on the inclined plane. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -C Objective (More than one option is correct)
7 Videos
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -D (Linked Comprehension)
12 Videos
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -A Objective (one option is correct)
50 Videos
- MOCK_TEST_17BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOCK_TEST_17EXERCISE - Example
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
Similar Questions
A particle is projected from the bottom of an inclined plane of inclination 30∘ with velocity of 40m/s at an angle of 60∘ with horizontal. Find the speed of the particle when its velocity vector is parallel to the plane. Take g=10m/s2.
View SolutionA particles is projected from the foot of an inclined plane having inclination 45∘ , with the velocity u at angle θ(>45∘) with the horizontal in a vertical plane containing the line of greatest slope through the point of projection. Find the value of tanθ if the particle stikes the plane.
(i) Horizontally
(ii) Normally
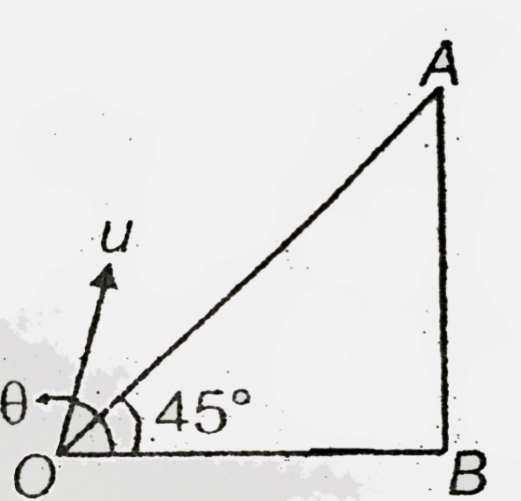
View SolutionA particle is projected up an inclined plane of inclination β at an elevation ∝ to the horizontal. Find the ratio between tan∝andtanβ, if the particle strikes the plane horizontally.
View SolutionA ball is projected from the bottom of an inclined plane of inclination 30∘, with a velocity of 30ms−1, at an angle of 30∘ with the inclined plane. If g=10ms−2 , then the range of the ball on given inclined plane is
View Solution
A particle is projected from surface of the inclined plane with speed u and at an angle θ with the horizontal. After some time the particle collides elastically with the smooth fixed inclined plane for the first time and subsequently moves in vertical direction. Starting from projection, find the time taken by the particle to reach maximum height. (Neglect time of collision).
View SolutionA projectile is projected upward with speed 2m/s on an incline plane of inclination 30∘ at an angle of 15∘ from the plane. Then the distance along the plane where projectile will fall is :
View SolutionA projectile is projected upward with speed 2m/s on an incline plane of inclination 30∘ at an angle of 15∘ from the plane. Then the distance along the plane where projectile will fall is :
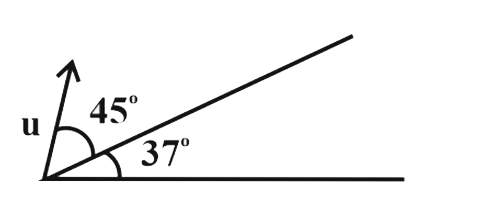
View SolutionA particle is projected on a frictionless inclined plane of inclination 37∘ at an angle of projection 45∘ from the inclined plane as shown in the figure. If after the first collision from the plane, the particle returns to its point of projection, then what is the value of the reciprocal of the coefficient of restitution between the particle and the plane?
View SolutionA particle is projected with a velocity u making an angle θ with the horizontal. The instantaneous power of the gravitational force
View SolutionA particle is projected up an inclined plane of inclination β at na elevation ∝ to the horizontal. Show that
(a) tan∝=cotβ+2tanβ, if the particle strikes the plane at right angles
(b) tan∝=2tanβ, if the particle strikes the plane horizontally.
View Solution