Determine the maximum acceleration of the truck in which a box lying on the floor of its back will remain stationary, given that the coefficient of static friction between the box and truck's floor is 0.2.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT ( SECTION -A)
50 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT ( SECTION -B) objective type questions (one option is correct)
59 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Illustration
7 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
Similar Questions
Detrmine the maximum acceleration of the train in which a box lying on the floor will remain stationary given that the coefficient of static friction between the box and the train s floor is 0.15 given g=10m/s2 .
View SolutionMaximum acceleration of the train in which a 50 kg box lying on its floor will ramain stationary is (Given: Co-efficient of static friction between the box and the train's floor is 0.3andg=10ms−2)
View SolutionA wooden box lying at rest on an inclined surface of a wet wood is held at static equilibrium by a constant force F applied perpendicular to the incline. If the mass of the box is 1kg, the angle of inclination is 30∘ and the coefficient of static friction between the box and the inclined plane is 0.2, the minimum magnitude of F is (Use g= 10m/s2 )
View SolutionA man of mass 75kg is pushing a heavy box on a flat floor. The coefficient of kinetic and static friction between the floor and the box is 0.20, and the coefficient of static friction between the man's shoes and the floor is 0.80. If the man pushes horizontally, what is the maximum values (in kg) of the box he can move?

View SolutionIn a rotor, a hollow vertical cylindrical structure rotates about its axis and a person rests against the inner wall. At a particular speed of the rotor, the floor below the person is removed and the person hangs resting against the wall without any floor. If the radius of the rotor is 2m and the coefficient of static friction between the wall and the person is 0.2, find the minimum speed at which the floor may be removed Take g=10ms2.
View SolutionIN a rotor, a hollow verticla cylindrical structure rotates about its axis and a person rests asgainst he inner wall. At a particular speed of the rotor, the floor below the person is removed and the person hangs resting against the wall without any floor. If the radius of the roter is 2m and the coefficient of static frictioin between the wall and theperson is 0.2, find the minimum speed at which the floor may be removed Take g=10ms2.
View SolutionA block of mass 1 kg is placed on a truck which accelerates with acceleration 5ms−2. The coefficient of static friction between the block and truck is 0.6. The frictional force acting on the block is
View SolutionThe coefficient of friction between two surface is 0.2. The maximum angle of friction is
View SolutionA block is placed at distance of 2m from the rear on the floor of a truck (g=10ms−2). When the truck moves with an acceleration of 8ms−2, the block takes 2 sec to fall off from the rear of the truck. The coefficient of sliding friction between truck and the block is
View SolutionA uniform beam of mass m is inclined at an angle θ to the horizontal. Its upper end produces a ninety degree bend in a very rough rope tied to a wall, and its lower end rests on a rough floor (a) If the coefficient of static friction between beam and floor is μs determine an expression for the maximum mass M that can be suspended from the top before the beam slips. (b) Determine the magnitude of the reaction force at the floor and the magnitude of the force exerted by the beam on the rope at P in terms of m,M and μs
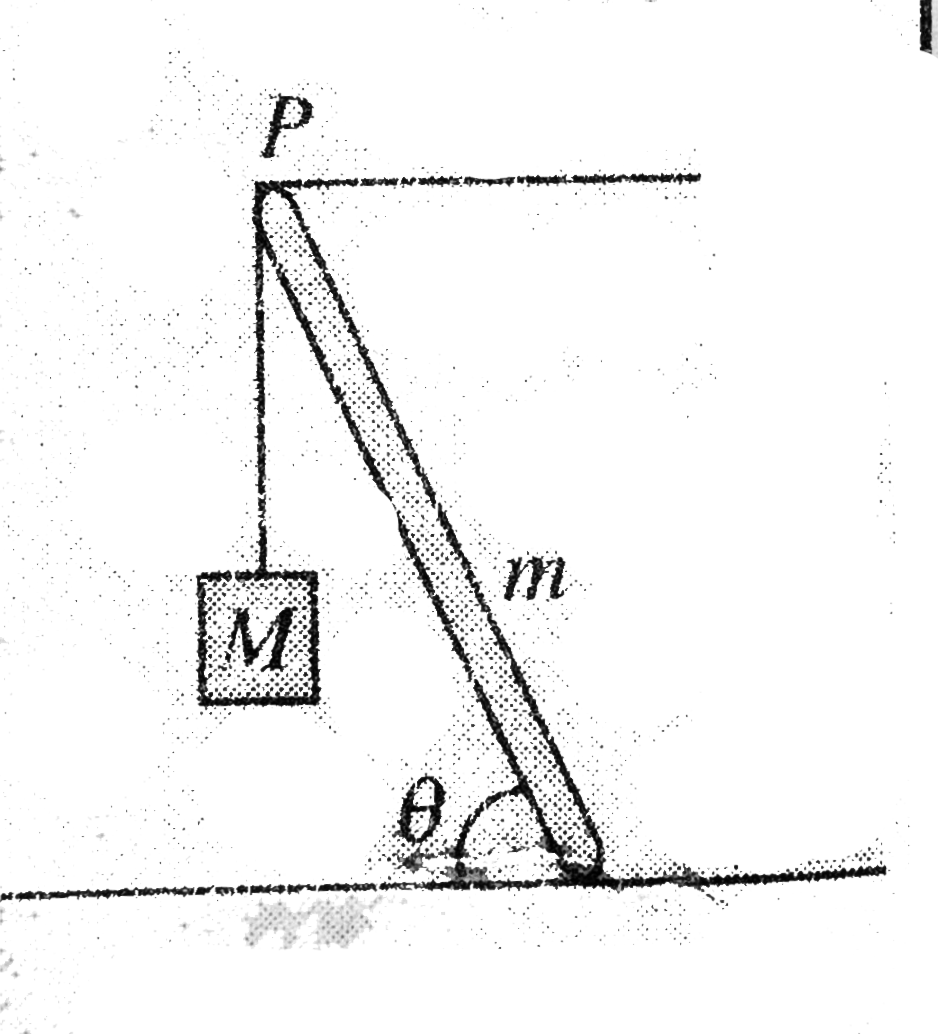 .
.
View Solution
