Maximum acceleration of the train in which a 50 kg box lying on its floor will ramain stationary is (Given: Co-efficient of static friction between the box and the train's floor is 0.3andg=10ms−2)
5.0ms−2
3.0ms−2
1.5ms−2
15ms−2
The correct Answer is:B
To solve the problem of finding the maximum acceleration of the train such that a 50 kg box remains stationary on its floor, we can follow these steps:
1. Identify the Given Data:
- Mass of the box, m=50kg
- Coefficient of static friction, μ=0.3
- Acceleration due to gravity, g=10m/s2
2. Calculate the Normal Force:
- The normal force N acting on the box is equal to its weight, which can be calculated using:
N=m⋅g=50kg⋅10m/s2=500N
3. Calculate the Maximum Frictional Force:
- The maximum static frictional force Ffriction that can act on the box is given by:
Ffriction=μ⋅N=0.3⋅500N=150N
4. Set Up the Equation for Pseudo Force:
- When the train accelerates, a pseudo force Fpseudo acts on the box in the opposite direction of the train's acceleration. This force can be expressed as:
Fpseudo=m⋅a
- Here, a is the acceleration of the train.
5. Equate the Pseudo Force to the Maximum Frictional Force:
- For the box to remain stationary relative to the train, the pseudo force must be equal to the maximum static frictional force:
m⋅a=Ffriction
- Substituting the values we have:
50kg⋅a=150N
6. Solve for the Maximum Acceleration a:
- Rearranging the equation gives:
a=150N50kg=3m/s2
Conclusion
The maximum acceleration of the train in which the 50 kg box will remain stationary is:
3m/s2
- Mass of the box, m=50kg
- Coefficient of static friction, μ=0.3
- Acceleration due to gravity, g=10m/s2
- The normal force N acting on the box is equal to its weight, which can be calculated using:
N=m⋅g=50kg⋅10m/s2=500N
- The maximum static frictional force Ffriction that can act on the box is given by:
Ffriction=μ⋅N=0.3⋅500N=150N
- When the train accelerates, a pseudo force Fpseudo acts on the box in the opposite direction of the train's acceleration. This force can be expressed as:
Fpseudo=m⋅a
- Here, a is the acceleration of the train.
- For the box to remain stationary relative to the train, the pseudo force must be equal to the maximum static frictional force:
m⋅a=Ffriction
- Substituting the values we have:
50kg⋅a=150N
- Rearranging the equation gives:
a=150N50kg=3m/s2
The maximum acceleration of the train in which the 50 kg box will remain stationary is:
3m/s2
Similar Questions
Detrmine the maximum acceleration of the train in which a box lying on the floor will remain stationary given that the coefficient of static friction between the box and the train s floor is 0.15 given g=10m/s2 .
View SolutionDetermine the maximum acceleration of the truck in which a box lying on the floor of its back will remain stationary, given that the coefficient of static friction between the box and truck's floor is 0.2.
View Solution
Knowledge Check
A block of mass 2 kg is placed on the floor. The coefficient of static friction is 0.4. A force F of 3 N is applied on the block as shown in figure. The force of friction between the block and the floor is (Take g=10ms−2)
 A3 NB8 NC4 ND6 N
A3 NB8 NC4 ND6 N
A wooden box lying at rest on an inclined surface of a wet wood is held at static equilibrium by a constant force F applied perpendicular to the incline. If the mass of the box is 1kg, the angle of inclination is 30∘ and the coefficient of static friction between the box and the inclined plane is 0.2, the minimum magnitude of F is (Use g= 10m/s2 )
View SolutionA car starts from rest at time t = 0 and it a-t graph is shown in figure. A coin is initially at rest on the floor of the car. At t = 1 s the coin begins to slip and it stops slipping at t = 3 s. The coefficient of static friction between the floor and the coin is (g = 10 m/s2)
_PHY_E05_188_Q02.png)
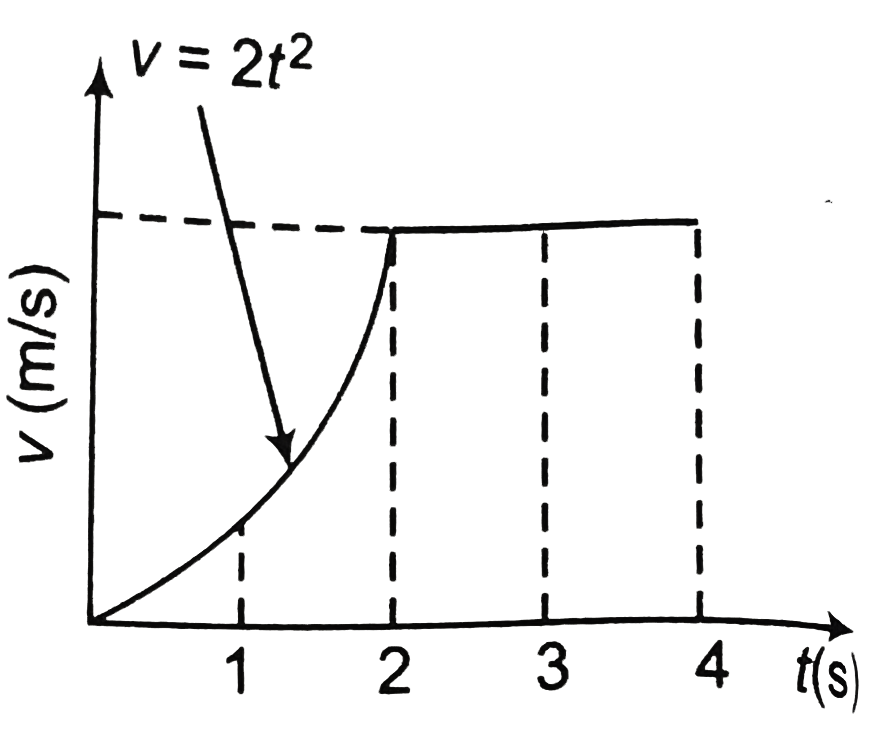
View SolutionA car begains from rest at time t=0, and then acceleration along a straight track during the interval 0<t≤2s and thereafter with constant velocity as shown in figure in the graph. A coin is initially at rest on the floor of the car. At t=1s, the coin begains to slip and its stops slipping at t=3s . The coefficient of static friction between the floor and the coin is (g=10m/s2)
View SolutionA block of mass 2kg lying on ice when given a velocity of 6ms−1 is stopped by friction in 5s. The coefficient of friction between the block and ice is (g=10 ms−2)
View SolutionA man holds a 2 kg book between his palms. so that each hand exerts the same horizontal force on the book. The coefficient of static friction between the palms and the book is 0.4 and g = 10ms−2. If the book is prevented from falling, the least force exerted by each hand on the book is
View SolutionA man of mass 75kg is pushing a heavy box on a flat floor. The coefficient of kinetic and static friction between the floor and the box is 0.20, and the coefficient of static friction between the man's shoes and the floor is 0.80. If the man pushes horizontally, what is the maximum values (in kg) of the box he can move?

View SolutionIn a rotor, a hollow vertical cylindrical structure rotates about its axis and a person rests against the inner wall. At a particular speed of the rotor, the floor below the person is removed and the person hangs resting against the wall without any floor. If the radius of the rotor is 2m and the coefficient of static friction between the wall and the person is 0.2, find the minimum speed at which the floor may be removed Take g=10ms2.
View Solution
