A bullet of mass A and velocity B is fired into a wooden block of mass C. If the bullet geta embedded in the wooden block.then velocity of wooden block after collision
A+BAC
A+CB+C
ACB+C
ABA+C
The correct Answer is:D
To solve the problem of finding the velocity of the wooden block after the bullet embeds into it, we can use the principle of conservation of momentum. Here’s a step-by-step solution:
Step 1: Understand the System
We have:
- A bullet of mass A and velocity B.
- A wooden block of mass C initially at rest.
Step 2: Write the Initial Momentum
Before the collision, the momentum of the system consists of the momentum of the bullet and the momentum of the wooden block. The wooden block is at rest, so its initial momentum is zero.
Initial Momentum=Momentum of Bullet+Momentum of Block=A×B+C×0=A×B
Step 3: Write the Final Momentum
After the bullet embeds into the wooden block, the total mass of the system becomes A+C and the final velocity of the combined system is Vf.
Final Momentum=(Mass of Bullet+Mass of Block)×Final Velocity=(A+C)×Vf
Step 4: Apply Conservation of Momentum
According to the law of conservation of momentum, the initial momentum of the system must equal the final momentum of the system:
A×B=(A+C)×Vf
Step 5: Solve for Final Velocity Vf
Rearranging the equation to solve for Vf:
Vf=A×BA+C
Final Answer
The velocity of the wooden block after the collision is:
Vf=A×BA+C
---
We have:
- A bullet of mass A and velocity B.
- A wooden block of mass C initially at rest.
Before the collision, the momentum of the system consists of the momentum of the bullet and the momentum of the wooden block. The wooden block is at rest, so its initial momentum is zero.
After the bullet embeds into the wooden block, the total mass of the system becomes A+C and the final velocity of the combined system is Vf.
According to the law of conservation of momentum, the initial momentum of the system must equal the final momentum of the system:
Rearranging the equation to solve for Vf:
The velocity of the wooden block after the collision is:
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT ( SECTION -B) objective type questions (one option is correct)
59 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT ( SECTION -C) objective type questions (More than one options are correct)
21 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - TRY YOURSELF
69 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
Similar Questions
A bullet of mass m and velocity v is fired into a large block of mass M. The final velocity of the system is
View SolutionA bullet of mass m moving with velocity υ1 strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height y. the initial of the bullet is

View Solution
Knowledge Check
A bullet of mass m moving horizontally with a velocity v strikes a block of wood of mass M and gets embedded in the block. The block is suspended from the ceiling by a massless string. The height to which block rises is
Av22g(mM+m)2Bv22g(M+mm)2Cv22g(mM)2Dv22g(Mm)2
Two blocks of masses m and 3m are connected by an inextensible string and the string passes over a fixed pulley which is massless and frictionless. A bullet of mass m moving with a velocity 'u' hits the hanging block of mass 'm' and gets exbedded in it. Find the height through which block A rises after the collision.
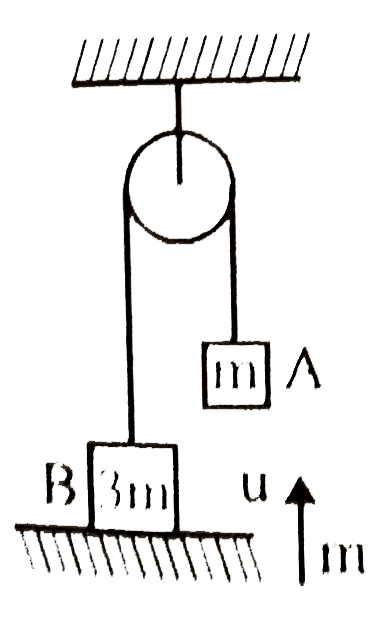
View SolutionA bullet of mass m strikes a block of mass M. The bullet remains embedded in the block. Find the amplitude of the resulting SHM.

View SolutionA bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
View SolutionTwo identical blocks A and B connected by massless string, are placed on a frictionless horizontal plane. A bullet havig the same mass, moving with speed u strickes block B from behind as shown. If the bullet gets embedded into block B then find

a. the velocity of A,B,C after collision.
b. impulse on A due to tension in the string,
c. impulse on C due to normal force of collision,
d. impulse on B due to normal force of collision.
View SolutionA frequently used device to measure the speed of bullets is the ballistic pendulum. It comprises of a heavy block of wood of mass M suspended by two long chords. A bullet of mass m is fired into the block horizontally. The block, with the bullet embedded in it, swings upwards. The centre of mass of the combination rises through a vertical distance h before coming to rest momentarily. In a particular experiment, a bullet of mass 40 gm is fired into a wooden block of mass 10 kg. The block is observed to rise by a height of 20.0 cm.
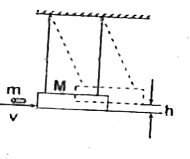
Fraction of initial energy lost in the collision
View SolutionA bullet of mass 0.25kg is fired with velocity 302m/s into a block of wood of mass m1=37.5kg. It gets embedded into it. The block m1 is resting on a long block m2 and the horizontal surface on which it is placed is smooth. The coefficient of friction between m1 and m2 is 0.5. Find the displacement of m1 on m2 and the common velocity of m1 and m2. Mass m2=1.25kg.
View Solution
A block of mass m is suspended from one end of a light spring as shown. The origin O is considered at distance equal to natural length of the spring from the ceiling and vertical downwards direction as positive y-axis. When the system is in equilibrium a bullet of mass m3 moving in vertical up wards direction with velocity v0 strikes the block and embeds into it. As a result, the block (with bullet embedded into it) moves up and start oscillating. Based on the given information, answer the following question:
Q. The time taken by the block bullet system to move from y=mgk (initial equilibrium position) to y=0 (natural length of spring) is (A represents the amplitude of motion)
View Solution
