Match the following
Column IColumn II(A)E∝1r2(p)Point charge(B)E∝r(q)Spherically symmetric charge distribution(C)V∝1r(r)Long line charge(D)V2−V1=f(r2r1)(s)Plane sheet of charge(E)V2−V1∝r2−r1(t)Electric dipole
The correct Answer is:A(p,q),B(q),C(p,q),D(r ),E(s)
To solve the matching question, we need to analyze the properties of electric fields and potentials for different charge distributions. Let's break down the information step by step.
Step 1: Analyze Point Charge
- For a point charge q:
- Electric field E is given by E∝1r2 (where r is the distance from the charge).
- Electric potential V is given by V∝1r.
Matching:
- This corresponds to option (p).
Step 2: Analyze Spherically Symmetric Charge Distribution
- For a spherically symmetric charge distribution:
- Electric field outside the sphere E is E∝1r2.
- Electric field inside the sphere E is E∝r.
- Electric potential outside the sphere V is V∝1r.
Matching:
- This corresponds to option (q).
Step 3: Analyze Long Line Charge
- For a long line charge:
- Electric field E is given by E∝1r.
- The potential difference V2−V1 can be expressed as V2−V1∝ln(r2r1).
Matching:
- This corresponds to option (r).
Step 4: Analyze Plane Sheet of Charge
- For a plane sheet of charge:
- Electric field E is constant and does not depend on r.
- The potential difference V2−V1 is proportional to r2−r1.
Matching:
- This corresponds to option (s).
Step 5: Analyze Electric Dipole
- For an electric dipole:
- Electric field E is given by E∝1r3.
- The potential difference V2−V1 is proportional to 1r22−1r21.
Matching:
- This corresponds to option (t).
Final Matching Summary:
- A matches with (p) (Point charge).
- B matches with (q) (Spherically symmetric charge distribution).
- C matches with (r) (Long line charge).
- D matches with (s) (Plane sheet of charge).
- E matches with (t) (Electric dipole).
Final Answer:
- A - p
- B - q
- C - r
- D - s
- E - t
- For a point charge q:
- Electric field E is given by E∝1r2 (where r is the distance from the charge).
- Electric potential V is given by V∝1r.
Matching:
- This corresponds to option (p).
- For a spherically symmetric charge distribution:
- Electric field outside the sphere E is E∝1r2.
- Electric field inside the sphere E is E∝r.
- Electric potential outside the sphere V is V∝1r.
Matching:
- This corresponds to option (q).
- For a long line charge:
- Electric field E is given by E∝1r.
- The potential difference V2−V1 can be expressed as V2−V1∝ln(r2r1).
Matching:
- This corresponds to option (r).
- For a plane sheet of charge:
- Electric field E is constant and does not depend on r.
- The potential difference V2−V1 is proportional to r2−r1.
Matching:
- This corresponds to option (s).
- For an electric dipole:
- Electric field E is given by E∝1r3.
- The potential difference V2−V1 is proportional to 1r22−1r21.
Matching:
- This corresponds to option (t).
- A matches with (p) (Point charge).
- B matches with (q) (Spherically symmetric charge distribution).
- C matches with (r) (Long line charge).
- D matches with (s) (Plane sheet of charge).
- E matches with (t) (Electric dipole).
- A - p
- B - q
- C - r
- D - s
- E - t
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-G(INTEGER ANSWER TYPE QUESTIONS)
9 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-H Multiple True-False Type Questions
4 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-E (Assertion-Reason Type Questios)
12 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
Similar Questions
Column I shows charge distribution and column II shows electrostatic field created by that charge at a point r distance from its centre.
(,Column I ,,Column II),((A),A stationary point charge,(p),E∝r0),((B),A stationary uniformly long charge rod,(q),E∝r1),((C),A stationary electric dipole,(r),E∝r⋅−1),,(s),E∝r−2),(,,(t),E∝r−3):}
View SolutionColumn I shows distributionof electric field liness and column II shows charge distribution . Match the columns.
Column I Column II(A)Straight lines but not parallel(p)Uniformly distributed charged shell(B)Straight lines but parallel (q)Uniformly distributed charged long rod(C)Curved lines(r)Uniformly distributed infinite charged sheet(D)Some regions where no lines are present(s)Electric dipole(t)Any conducting material
View SolutionMatch the column :
A particle at a distance r from the centre of a uniform spherical planet of mass M radius R(<r) has a velocity v magnitude of which is given in column I. Match trajectory from column II about possible nature of orbit.
Column IColumn II(A)0<V<√GMr(P)Straight line(B)√GMr(Q)Circle(C)√2GMr(R)Parabola(D)v>√2GMr(S)Ellipse
View SolutionOn the surface of earth acceleration due gravity is g and gravitational potential is V. Match of following columns
Column-IColumn-II(A)At height h=R, value of g(p)Decreases by a factor14(B)At depth h=R2,value of g(q)Decrease by a factor12(C)At height h=R,value of V(r)Increase by a factor118(D)At height h=R2,value of V(s)Increase by a factor 2(t)None
View SolutionName the types of interaction or intermolecular forces of which potential energy-distance function are given below
(a) E∝1r (b) E∝1r2 (c ) E∝1r3
(d) E∝1r4 (e) E∝1r6 .
View SolutionLet Rt represents activity of a sample at an insant and Nt represent number of active nuclei in the sample at the instant. T1/2 represents the half life.
Column IColumn II(A)t=T1/2(p)Rt=R02(B)t=T1/2ln2(q)N0−Nt=N02(C)t=32T1/2(r)Rt−R0R0=1−ee(s)Nt=N02√2
View SolutionA sphere S1 of radius r1 encloses a total charge Q. If there is another concentric sphere S2 of radius r2(>r1) and there be no additional charges between S1andS2 find the ratio of electric flux through S1andS2,
View SolutionDraw E-r and V-r graphs due to two charged spherical shells as shown in figure (along the line between C and ∝)

View SolutionConsider two charged metallic spheres S1, and S2, of radii R1, and R2 respectively. The electric fields E1, (on S1,) and E2, (on S2) their surfaces are such that E1/E2=R1/R2. Then the ratio V1(on S1)/V2 (on S2) of the electrostatic potential on each sphere is
View SolutionIn the diagram shown in figure mass of both the balls in same. Match the following columns.
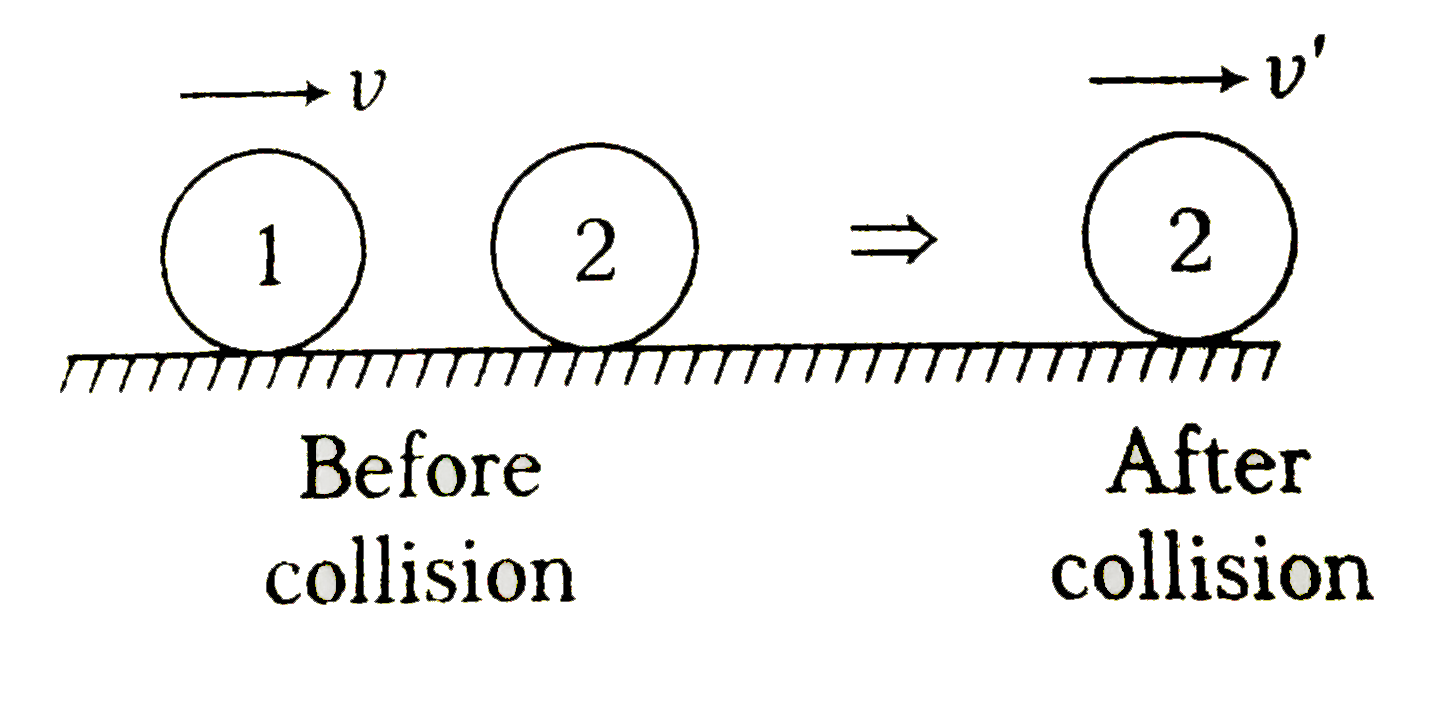
Column1Column2A Forv′=vP e=0B Forv′=v/2Q e=1C Forv′=3/4vR e=1/2-(S data is insufficient
View Solution
