Consider these three statements for a capacitor
STATEMENT-1 Capacitance of a capacitor must increase when a dielectric is inserted in between the capacitor plates.
STATEMENT-2 Potential differenece across a charged capacitor must increase if a dielectric is inserted in between the capacitor plates.
STATEMENT-3 Electrostatic energy stored by the capacitor may increase if a dielectric inserted in between the capacitor plates
T F F
F T F
T F T
F T T
The correct Answer is:C
To analyze the three statements regarding a capacitor, we will evaluate each statement step by step.
Step 1: Evaluate Statement 1
Statement 1: Capacitance of a capacitor must increase when a dielectric is inserted in between the capacitor plates.
Solution:
- The capacitance C of a capacitor without a dielectric is given by the formula:
C0=ϵ0Ad
where A is the area of the plates, d is the distance between them, and ϵ0 is the permittivity of free space.
- When a dielectric material with dielectric constant k is inserted, the new capacitance C becomes:
C=k⋅C0=k⋅ϵ0Ad
- Since k>1, it follows that C>C0. Therefore, the capacitance increases when a dielectric is inserted.
Conclusion: Statement 1 is True.
Step 2: Evaluate Statement 2
Statement 2: Potential difference across a charged capacitor must increase if a dielectric is inserted in between the capacitor plates.
Solution:
- Consider a charged capacitor with charge Q and initial capacitance C0. The initial potential difference V0 is given by:
V0=QC0
- When a dielectric is inserted and if the capacitor is isolated (battery removed), the charge Q remains constant, but the capacitance changes to C=k⋅C0.
- The new potential difference V′ becomes:
V′=QC=Qk⋅C0=V0k
- Since k>1, it follows that V′<V0. Therefore, the potential difference decreases when a dielectric is inserted.
Conclusion: Statement 2 is False.
Step 3: Evaluate Statement 3
Statement 3: Electrostatic energy stored by the capacitor may increase if a dielectric is inserted in between the capacitor plates.
Solution:
- The electrostatic energy U stored in a capacitor is given by:
U=12CV2
- If the battery remains connected while inserting the dielectric, the capacitance changes to C=k⋅C0 and the potential V remains constant.
- The new energy U′ becomes:
U′=12(k⋅C0)V2=k⋅(12C0V2)=k⋅U
- Since k>1, it follows that U′>U. Therefore, the energy stored increases when a dielectric is inserted, provided the battery remains connected.
Conclusion: Statement 3 is True.
Final Summary
- Statement 1: True
- Statement 2: False
- Statement 3: True
Thus, the correct answer is that Statement 1 and Statement 3 are true, while Statement 2 is false.
---
Statement 1: Capacitance of a capacitor must increase when a dielectric is inserted in between the capacitor plates.
- The capacitance C of a capacitor without a dielectric is given by the formula:
C0=ϵ0Ad
where A is the area of the plates, d is the distance between them, and ϵ0 is the permittivity of free space.
- When a dielectric material with dielectric constant k is inserted, the new capacitance C becomes:
C=k⋅C0=k⋅ϵ0Ad
- Since k>1, it follows that C>C0. Therefore, the capacitance increases when a dielectric is inserted.
Statement 2: Potential difference across a charged capacitor must increase if a dielectric is inserted in between the capacitor plates.
- Consider a charged capacitor with charge Q and initial capacitance C0. The initial potential difference V0 is given by:
V0=QC0
- When a dielectric is inserted and if the capacitor is isolated (battery removed), the charge Q remains constant, but the capacitance changes to C=k⋅C0.
- The new potential difference V′ becomes:
V′=QC=Qk⋅C0=V0k
- Since k>1, it follows that V′<V0. Therefore, the potential difference decreases when a dielectric is inserted.
Statement 3: Electrostatic energy stored by the capacitor may increase if a dielectric is inserted in between the capacitor plates.
- The electrostatic energy U stored in a capacitor is given by:
U=12CV2
- If the battery remains connected while inserting the dielectric, the capacitance changes to C=k⋅C0 and the potential V remains constant.
- The new energy U′ becomes:
U′=12(k⋅C0)V2=k⋅(12C0V2)=k⋅U
- Since k>1, it follows that U′>U. Therefore, the energy stored increases when a dielectric is inserted, provided the battery remains connected.
- Statement 1: True
- Statement 2: False
- Statement 3: True
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-I Subjective Type Questions
6 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-J Aakash Challengers Questions
5 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-G(INTEGER ANSWER TYPE QUESTIONS)
9 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
Similar Questions
STATEMENT-1 : If the distance plates of a charged isolated capacitor increases, then the potential energy in the electric field of capacitor increases.
and
STATEMENT-2 : The energy stored in a capacitor is always directly proportional to separation between the plates.
View SolutionWhen a dielectric slab is inserted between the plates of one of the two identical capacitors in figure , which of the following properties increase ?
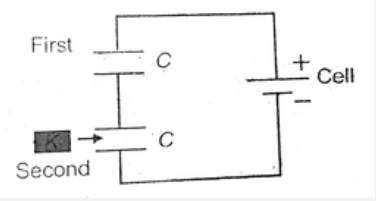
View SolutionA capacitor and a bulb are connected in series with a source of alternating emf. If a dielectric slab is inserted between the plates of the capacitor, then
View SolutionThe potential enery of a charged parallel plate capacitor is U0. If a slab of dielectric constant K is inserted between the plates, then the new potential energy will be
View SolutionThe potential enery of a charged parallel plate capacitor is U0. If a slab of dielectric constant K is inserted between the plates, then the new potential energy will be
View SolutionWhen a dielectric slab is inserted between the plates of one of the two identical capacitors shown in the figure then match the following:
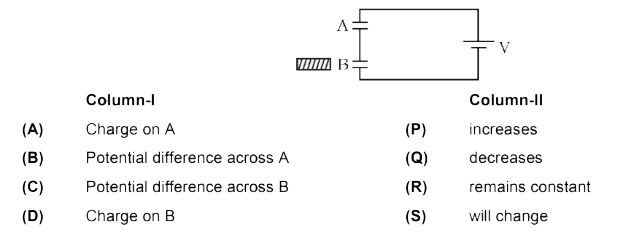
View SolutionIn a parallel plate capacitor, the distance between the plates is d and potential difference across the plate is V. Energy stored per unit volume between the plates of capacitor is
View SolutionA dielectric slab is inserted between the plates of a capacitor. The charge on the capacitor is Q and the magnitude of the induced charge on each surface of the dielectric is Q'.
View SolutionA dielectric slab is inserted between the plates of an isolated capacitor. The force between the plates will
View SolutionA dielectric slab is inserted between the plates of an isolatted charged capacitor. Which of the following quantities will remain the same?
View Solution
