Two parallel infinite line charges with linear charge densities +λC/m and −λ C/m are placed at a distance of 2R in free space. What is the electric field mid-way between the two line charges?
zero
2λπε0R
λπε0R
12πε0R
The correct Answer is:B
To find the electric field midway between two parallel infinite line charges with linear charge densities +λ C/m and −λ C/m, we can follow these steps:
Step 1: Understand the Configuration
We have two infinite line charges:
- The first line charge has a positive linear charge density +λ C/m.
- The second line charge has a negative linear charge density −λ C/m.
- The distance between the two line charges is 2R.
Step 2: Identify the Midpoint
The midpoint between the two line charges is at a distance of R from each line charge.
Step 3: Calculate the Electric Field Due to Each Line Charge
The electric field E due to an infinite line charge with linear charge density λ at a distance r from the line charge is given by the formula:
E=2kλr
where k is Coulomb's constant, k=14πϵ0.
Electric Field from the Positive Line Charge
At the midpoint (distance R from the positive line charge):
E+=2kλR
This electric field is directed away from the positive line charge (repulsive).
Electric Field from the Negative Line Charge
At the midpoint (distance R from the negative line charge):
E−=2kλR
This electric field is directed towards the negative line charge (attractive).
Step 4: Determine the Direction of the Electric Fields
Since both electric fields are directed towards the same direction (let's assume the positive line charge is on the left and the negative line charge is on the right), they will add up.
Step 5: Calculate the Net Electric Field
The net electric field Enet at the midpoint is the sum of the magnitudes of the two electric fields:
Enet=E++E−=2kλR+2kλR=4kλR
Step 6: Substitute the Value of k
Substituting k=14πϵ0:
Enet=4⋅14πϵ0λR=λπϵ0R
Step 7: Final Result
The electric field midway between the two line charges is:
Enet=λπϵ0R^i
We have two infinite line charges:
- The first line charge has a positive linear charge density +λ C/m.
- The second line charge has a negative linear charge density −λ C/m.
- The distance between the two line charges is 2R.
The midpoint between the two line charges is at a distance of R from each line charge.
The electric field E due to an infinite line charge with linear charge density λ at a distance r from the line charge is given by the formula:
E=2kλr
where k is Coulomb's constant, k=14πϵ0.
At the midpoint (distance R from the positive line charge):
E+=2kλR
This electric field is directed away from the positive line charge (repulsive).
At the midpoint (distance R from the negative line charge):
E−=2kλR
This electric field is directed towards the negative line charge (attractive).
Since both electric fields are directed towards the same direction (let's assume the positive line charge is on the left and the negative line charge is on the right), they will add up.
The net electric field Enet at the midpoint is the sum of the magnitudes of the two electric fields:
Enet=E++E−=2kλR+2kλR=4kλR
Substituting k=14πϵ0:
Enet=4⋅14πϵ0λR=λπϵ0R
The electric field midway between the two line charges is:
Enet=λπϵ0R^i
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Taking it together
105 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Assertion and Reason
15 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.4
10 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
Two infinitely long thin straight wires having uniform linear charge densities λ and 2λ are arranged parallel to each other at a distance r apart.The intensity of the electric field at a point midway between them is
View SolutionA long charged cylinder of linear charge density λ is surrounded by a hollow co-axial conducting cylinder. What is the electric field in the space between the two cylinders ?
View Solution
Knowledge Check
Two parallel infinite line charges +λand−λ are placed with a separation distance R in free space. The net electric field exactly mid-way between the two line charges is
AzeroB2λπε0RCλπε0RDλ2πε0R
A long charged cylinder of linear charge density λ is surrounded by a hollow co-axial conducting cylinder. What is the electric field in the space between the two cylinders ?
View SolutionTwo uniformly long charged wires with linear densities λ and 3λ are placed along X and Y axis respectively. Determined the slope of electric field at any point on the l ine y=√3x
View SolutionTwo infinite line charges with uniform linear charge densities +λ&−λ are kept in such a way that the angle between them is 30∘. The electric field at the symmetric point P at a perpendicular distance r from each line charge is given by:
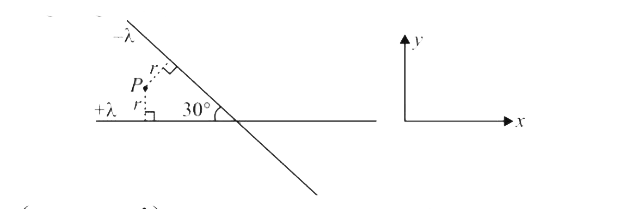
View SolutionTwo infinite line charges with uniform linear charge densities +λ&−λ are kept in such a way that the angle between them is 30∘. The electric field at the symmetric point P at a perpendicular distance r from each line charge is given by:

View SolutionBetween two infinitely long wires having linear charge densities λ and −λ , there are two points A and B as shown in the figure. The amount of work done by the electric field in moving a point charge q0 from A to B is equal to :

View SolutionAn infinitely long wire with linear charge density +λ is bent and the two parts are inclined at angle 30∘ as shown in fig, the electric field at point P is :
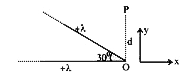
View SolutionTwo infinitely long parallel wires having linear charge densities λ1 and λ2 respectively are placed at a distance of R metres. The force per unit length on either wire will be (k=14πε0)
View Solution
