Two long co-axial cylinderical metal tubes ( inner radius a, outer radius b ) stand vertically in a tank of dielectric oil ( dielectric constant k and density ρ). Constant potential difference is maintained between tubes by means of a cell as shown in figure. To what height ( h ) does the oil rise in the space between the tubes.
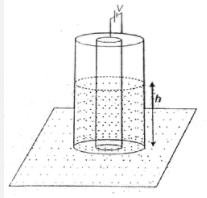
h=2v2ε0(k−1)ρg(b2−a2)ln(ba)
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - EXAMPLE
138 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - EXERCISE
20 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-I Subjective Type Questions
6 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
Similar Questions
Two long coaxial cylindrical metal tubes (inner radius a, outer radius b) stand vertically in a tank of dielectric oil (of mass density ρ , dielectric constant K). The inner one is maintained at potential V and the outer one is grounded. To what equilibrium height (h) does the oil rise in the space between the tubes? [Assume this height ( h) as an equilibrium height]
View SolutionTwo long coaxial and conducting cylinders of radius a and b are separated by a material of conductivity σ and a constant potential difference V is maintained between them by a battery. Then the current per unit length of the cylinder flowing from one cylinder to the other is
View Solution
Knowledge Check
Two long coaxial cylindrical metal tubes (inner radius a, outer radius b) stand vertically in a tank of dielectric oil (of mass density ρ , dielectric constant K). The inner one is maintained at potential V and the outer one is grounded. To what equilibrium height (h) does the oil rise in the space between the tubes? [Assume this height ( h) as an equilibrium height]
Aε02V2(K−1)gρ(b2−a2)1n(ba)Bε02V2(K−1)ρ(b2−a2)g1n(ba)C4ε02V2(K−1)gρ(b2−a2)1n(ba)D6ε02V2(K−1)ρ(b2−a2)g1n(ba)Two long coaxial cylindrical metal tubes stand on an insulatiog floor as shown in figure. A dielectric oil is filled in the annular region between the tubes. The tubes are maintained at a constant potential difference V. A small hole is opened at bottom then :
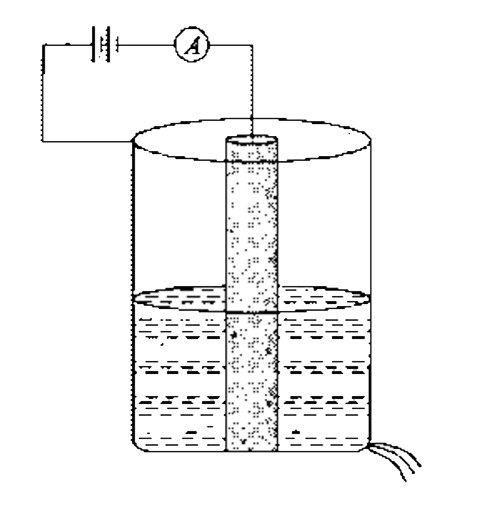 AReading of ammeter remain constantBCapacitance of system increasesCCurrent in circuit is dependent on area ofholeDCurrent in circuit is inversely proportional to dielectric constant
AReading of ammeter remain constantBCapacitance of system increasesCCurrent in circuit is dependent on area ofholeDCurrent in circuit is inversely proportional to dielectric constantTwo long coaxial and conducting cylinders of radius a and b are separated by a material of conductivity σ and a constant potential difference V is maintained between them, by a battery. Then the current, per unit length of the cylinder flowing from one cylinder to the other is
A4πσln(b/a)VB4πσ(b+a)VC2πσln(b/a)VD2πσ(b+a)V
Consider a hollow cylinder of length L and inner radius a and outer radius b, as shown in figure. The material has resistivity ρ.
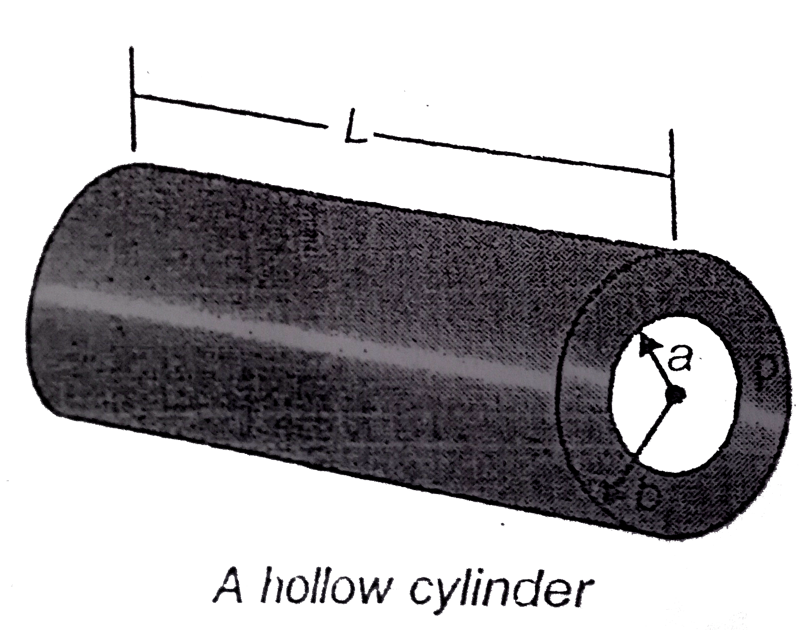
(a) Suppose a potential difference is applied between te ends of the cylinder and produces a current parallel to the axis. What is the resistance measure ?
(b) If instead the potential difference is applied between the inner outer surfaces so that current flows radially outward, what is the resistance measure ?
View SolutionTwo long cylindrical metal tubes stand on insulating floor. A dielectric oil is filled between plates. Two tubes are maintained with potential difference v. A small hole is opened at bottom then
View SolutionA cylindrical tube of length l has inner radius a while outer radius b. What is the resistance of the tube between (a) its ends (b) inner and outer surfaces ? (The resistivitiy of its material is p)
View SolutionIn the figure shown capacitors A and B of capacitance C are in steady state. A dielectric slab of dielectric constant K=2 and dimensions equal to the inner dimensions of the capcitors is inserted in the space between the plate of the capacitor B. In steady state choose the correct options.
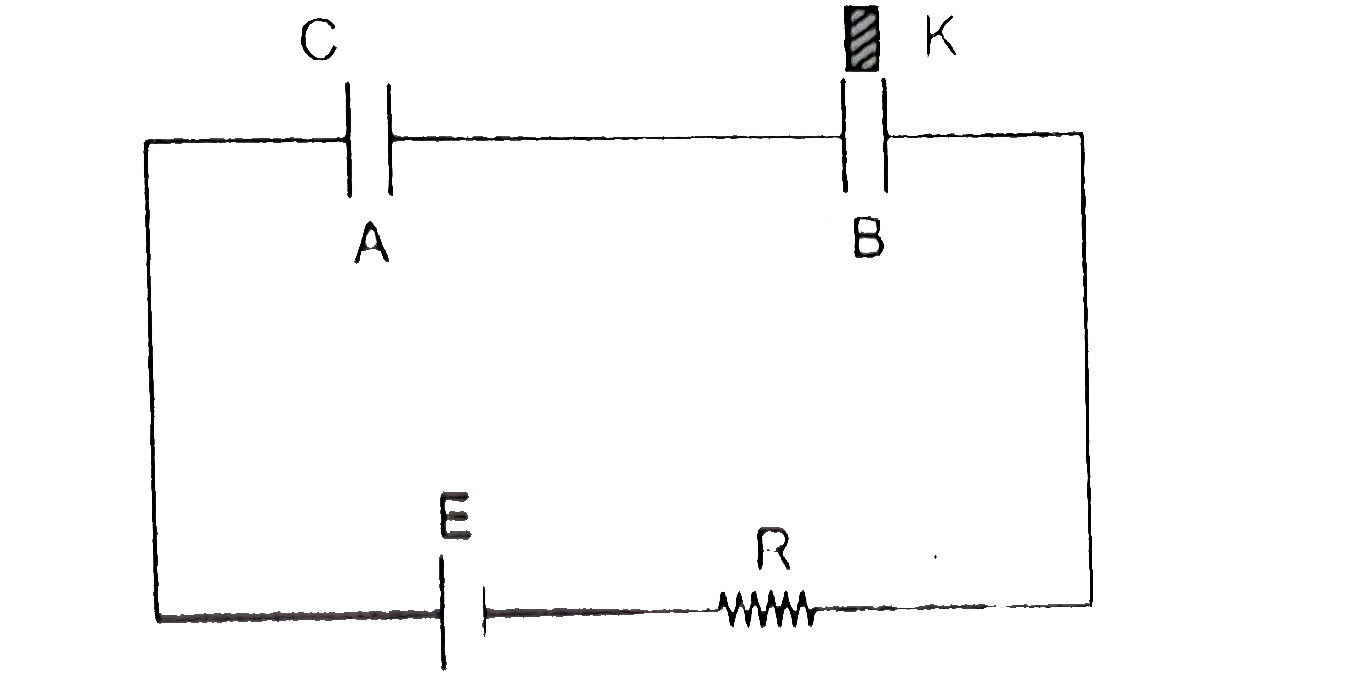
View SolutionTwo long coaxial and conducting cylinders of radius a and b are separated by a material of conductivity σ and a constant potential difference V is maintained between them by a battery. Then the current per unit length of the cylinder flowing from one cylinder to the other is
View Solution
