An infinitely long thin straight wire has uniform linear charge density of 1/4 coul m−1. Then the magnitude of the electric intensity at a point 18 cm away is
0.33×1011NC−1
3×1011NC−1
0.25×1011NC−1
1.32×1011NC−1
The correct Answer is:A
To solve the problem of finding the electric field intensity at a point 18 cm away from an infinitely long thin straight wire with a uniform linear charge density of λ=14C/m, we can follow these steps:
Step 1: Understand the Formula for Electric Field Intensity
The electric field intensity E due to an infinitely long straight wire with linear charge density λ is given by the formula:
E=λ2πϵ0r
where:
- E is the electric field intensity,
- λ is the linear charge density,
- ϵ0 is the permittivity of free space, approximately 8.85×10−12C2/N m2,
- r is the perpendicular distance from the wire.
Step 2: Convert Units
Convert the distance from centimeters to meters:
r=18cm=0.18m
Step 3: Substitute Values into the Formula
Substituting the values into the formula:
- λ=14C/m
- ϵ0=8.85×10−12C2/N m2
- r=0.18m
The electric field intensity becomes:
E=142π(8.85×10−12)(0.18)
Step 4: Calculate the Electric Field Intensity
Calculating the denominator:
2πϵ0r=2π(8.85×10−12)(0.18)
Calculating this gives:
2π(8.85×10−12)(0.18)≈1.005×10−10N m2/C2
Now substituting back into the equation for E:
E=0.251.005×10−10≈2.487×109N/C
Step 5: Final Result
Thus, the magnitude of the electric field intensity at a point 18 cm away from the wire is approximately:
E≈2.487×109N/C
The electric field intensity E due to an infinitely long straight wire with linear charge density λ is given by the formula:
E=λ2πϵ0r
where:
- E is the electric field intensity,
- λ is the linear charge density,
- ϵ0 is the permittivity of free space, approximately 8.85×10−12C2/N m2,
- r is the perpendicular distance from the wire.
Convert the distance from centimeters to meters:
r=18cm=0.18m
Substituting the values into the formula:
- λ=14C/m
- ϵ0=8.85×10−12C2/N m2
- r=0.18m
E=142π(8.85×10−12)(0.18)
Calculating the denominator:
2πϵ0r=2π(8.85×10−12)(0.18)
Calculating this gives:
2π(8.85×10−12)(0.18)≈1.005×10−10N m2/C2
E=0.251.005×10−10≈2.487×109N/C
Thus, the magnitude of the electric field intensity at a point 18 cm away from the wire is approximately:
E≈2.487×109N/C
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Exercise
57 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Exercise-I
80 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - AAKASH SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - PRACTICE EXERCISEX
42 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)
26 Videos
Similar Questions
An infinitely long thin straight wire has uniform linear charge density of 1/3coulm−1 .Then the magnitude of the electric intensity at a point 18cm away is
View SolutionA long thin flat sheet has a uniform surface charge density σ. The magnitude of the electric field at a distance .r. from it is given by
View Solution
Knowledge Check
If a long straight wire carries a current of 40 A, then the magnitude of the field B at a point 15 cm away from the wire is
A5.34×10−5TB8.34×10−5TC9.6×10−5TD10.2×10−5T
If the linear charge density of a cylinder is 4μCm−6 ,then electric field intensity at point 3.6 cm from axis is :
View SolutionFigure shows a long wire having uniform charge density λ as shown in figure. Calculate electric field intensity at point P.
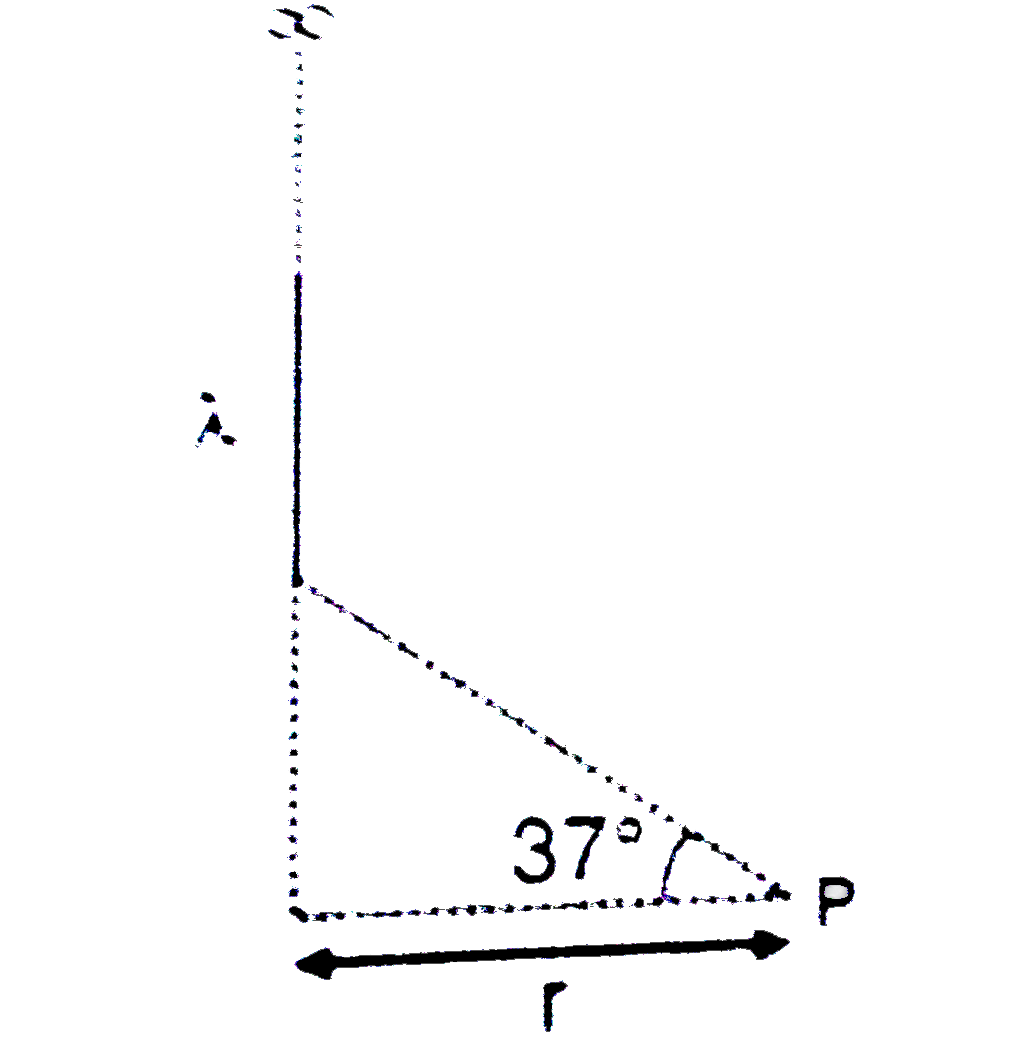
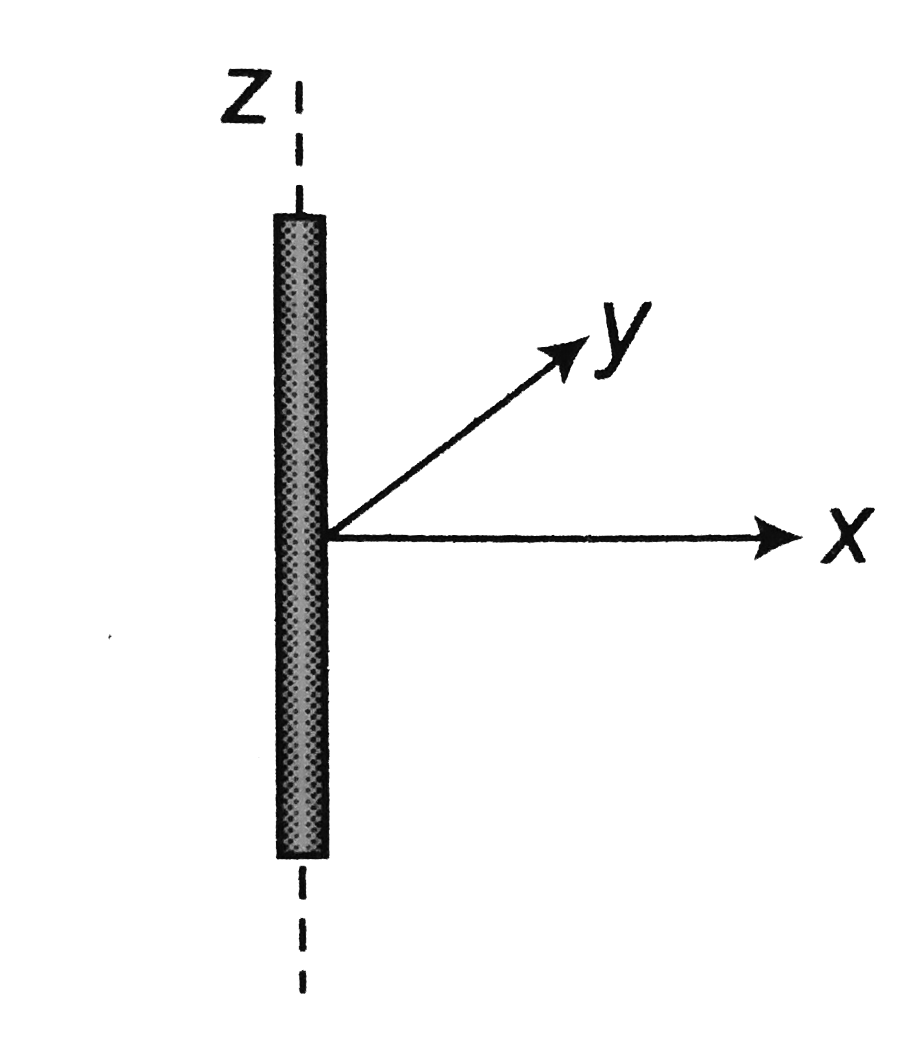
View SolutionAn infinitely long wire is kept along z-axis from z=−∞ to z=∞, having uniform linear charge density 109nC/m. The electric field at point (6cm,8cm,10cm) will be
View SolutionA long wire with a uniform charge density λ is bent in two configurations shown in fig. Determine the electric field intensity at point O.
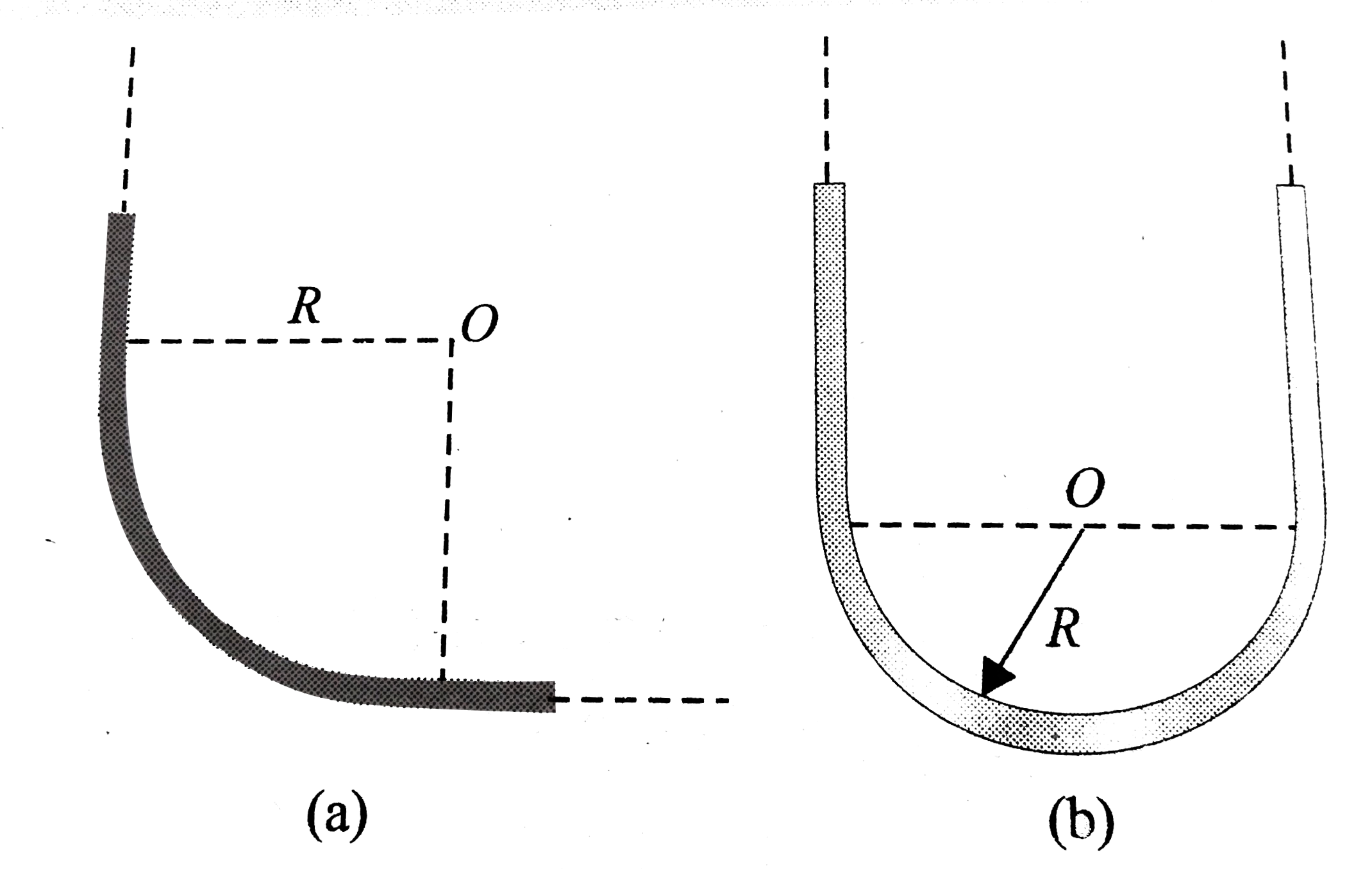
View SolutionAn infinitely long wire is kept along z-axis from z=∞ to z=∞, having uniform linear cahrges density 109nC/m. The electric field at point (6cm,8cm,10cm) will be

View SolutionAn infinitely long wire is kept along z-axis from z=∞ to z=∞, having uniform linear cahrges density 109nC/m. The electric field at point (6cm,8cm,10cm) will be

View SolutionA long straight wire carries a current of 35A. What is the magnitude of the field →B at a point 20cm from the wire?
View Solution
