A cell supplies a current of 2A to an exertnal resistance of 2Ω and a current of 1 ampere to another external resistance of 4.5Ω connected across the cell separately . Select the correct alternative (s).
Emf of the cell is 5 V
Emf of the cell is 4.25 V
Internal resistance of the cell is 0.5 Ω
Internal resistace of the cell is 3.25Ω
The correct Answer is:(1, 3)
To solve the problem, we need to find the electromotive force (emf) E and the internal resistance r of the cell based on the given currents and external resistances.
Step 1: Analyze the first case
In the first case, the cell supplies a current I1=2A to an external resistance R1=2Ω.
Using Ohm's law, we can express the emf E as:
E=I1⋅(R1+r)
Substituting the known values:
E=2⋅(2+r)
This simplifies to:
E=4+2r(Equation 1)
Step 2: Analyze the second case
In the second case, the cell supplies a current I2=1A to an external resistance R2=4.5Ω.
Again, using Ohm's law, we can express the emf E as:
E=I2⋅(R2+r)
Substituting the known values:
E=1⋅(4.5+r)
This simplifies to:
E=4.5+r(Equation 2)
Step 3: Set the equations equal
Since both expressions represent the same emf E, we can set Equation 1 equal to Equation 2:
4+2r=4.5+r
Step 4: Solve for internal resistance r
Rearranging the equation gives:
2r−r=4.5−4
r=0.5Ω
Step 5: Substitute r back to find E
Now that we have r, we can substitute it back into either Equation 1 or Equation 2 to find E. Using Equation 1:
E=4+2(0.5)=4+1=5V
Conclusion
The emf of the cell is 5V and the internal resistance is 0.5Ω.
Final Answers
- Emf E=5V
- Internal Resistance r=0.5Ω
In the first case, the cell supplies a current I1=2A to an external resistance R1=2Ω.
E=I1⋅(R1+r)
Substituting the known values:
E=2⋅(2+r)
This simplifies to:
E=4+2r(Equation 1)
In the second case, the cell supplies a current I2=1A to an external resistance R2=4.5Ω.
E=I2⋅(R2+r)
Substituting the known values:
E=1⋅(4.5+r)
This simplifies to:
E=4.5+r(Equation 2)
Since both expressions represent the same emf E, we can set Equation 1 equal to Equation 2:
4+2r=4.5+r
Rearranging the equation gives:
2r−r=4.5−4
r=0.5Ω
Now that we have r, we can substitute it back into either Equation 1 or Equation 2 to find E. Using Equation 1:
E=4+2(0.5)=4+1=5V
The emf of the cell is 5V and the internal resistance is 0.5Ω.
- Emf E=5V
- Internal Resistance r=0.5Ω
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT SECTION-D( LINKED COMPREHENSION TYPE QUESTIONS)
3 Videos
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT SECTION-D( LINKED COMPREHENSION TYPE QUESTIONS) Comprehension - II
5 Videos
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT SECTION-B(OBJECTIVE TYPE QUESTION ))
44 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COMMUNICATION SYSTEMS EXERCISE - ASSIGNMENT SECTION D (Assertion-Reason)
10 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
Similar Questions
The internal resistance of a 2.1 V cell which gives a current of 0.2A through a resistance of 10Ω is
View SolutionA cell supplies a current i1 trhough a resistnace R1 and a current i2 through a resistance R2. The internal resistance of this cell is
View Solution24 cells, each of emf 1.5V and internal resistance is 2Ω connected to 12Ω series external resistance. Then,
View SolutionThe internal resistance of a 2.1V cell which gives a current 0.2A through a resistance of 10Ω
View SolutionThe cell has an emf of 2V and the internal resistance of this cell is 0.1Ω, it is connected to resistance of 3.9Ω, the voltage across the cell will be
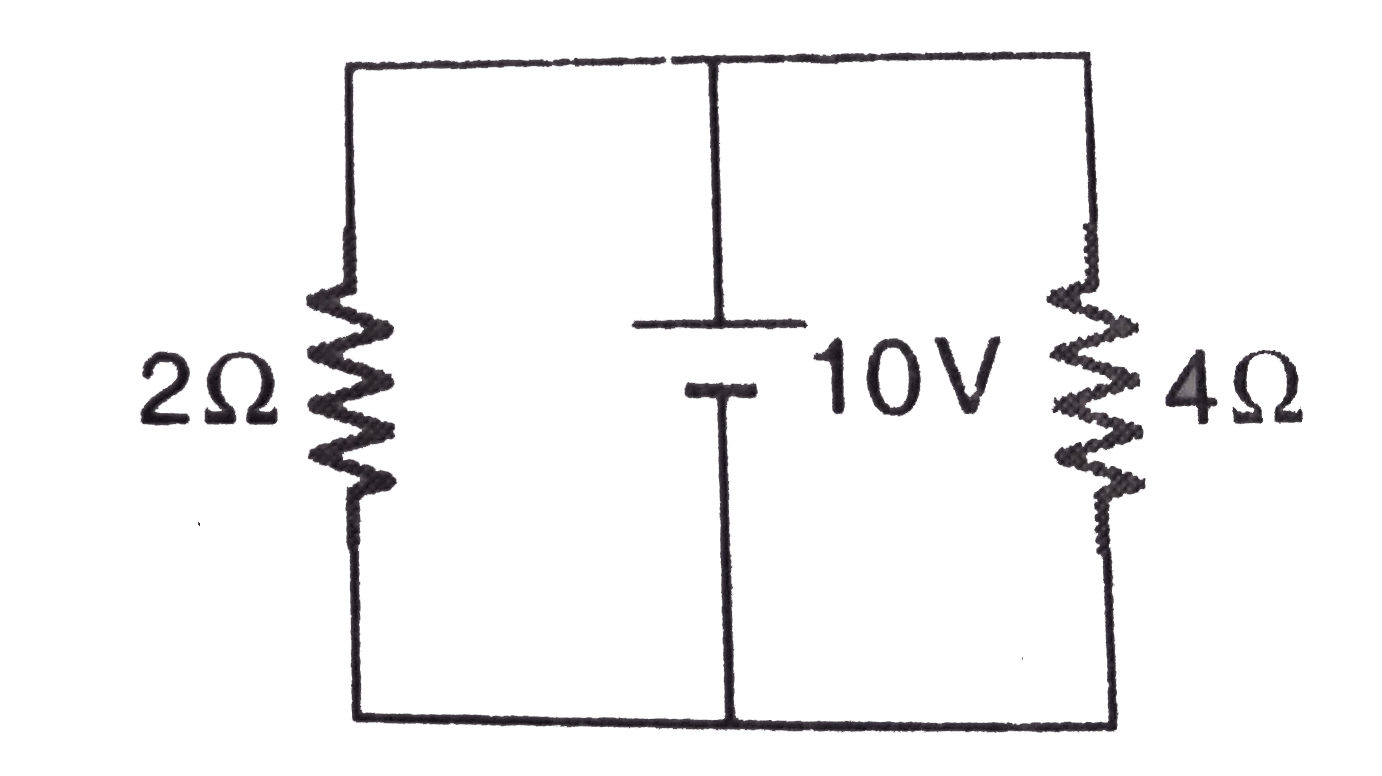
View SolutionFind the current through 2Ω and 4Ω resistance.
View SolutionA cell supplies a current of 2 A when it is connected to a 5Ω resistance and supplies a current of 1.2 A, if it is connected to a resistance of 9 Ω. Find the e.m.f and internal resistance of the cell.
View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance 1.5(Ω). Find the current flow through battery ?
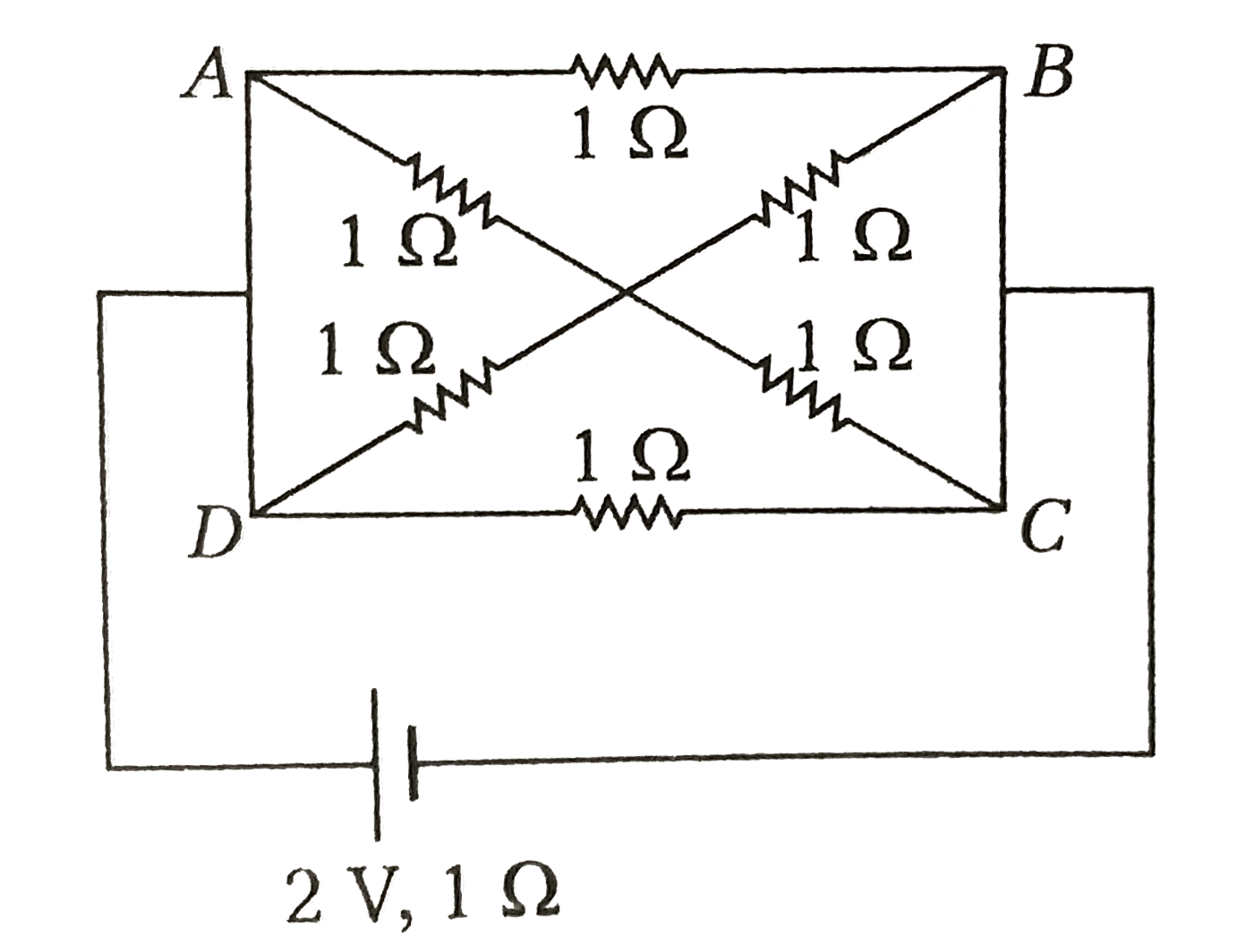
View SolutionFind the current drawn from a cell of emf 2 V and internal resistance 2Ω connected to the network given below.
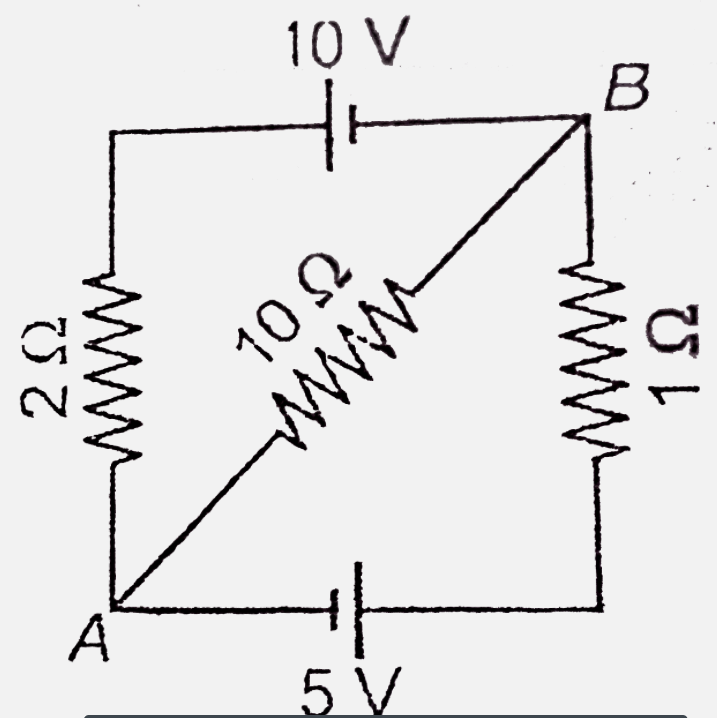
View SolutionFind the current through the 10Ω resistance connected across AB
View Solution
