A capacitor is charged to a potential difference of 100 V and is then connected across a resistor. The potential difference across the capacitor decays exponentially with respect to time. After 1 sec, the P.D. between the plates of the capacitor is 80 V. what will be the potential difference between the plates after 2 sec ?
After 2ms from start, the potential difference across the resistor is 64 V
After 2ms from start, the potential difference across the capacitor is 64 V
After 2ms from start , the potential difference across the resistor is 60V
After 2ms from start , the potential difference across the capacitor is 60 V
The correct Answer is:(1, 2 )
To solve the problem, we need to understand the exponential decay of the potential difference (P.D.) across a capacitor when it is discharged through a resistor. The voltage across the capacitor can be described by the equation:
V(t)=V0e−t/(RC)
Where:
- V(t) is the voltage at time t,
- V0 is the initial voltage (100 V in this case),
- R is the resistance,
- C is the capacitance,
- t is the time.
Step 1: Determine the decay constant 1RC
From the problem, we know that after 1 second, the voltage is 80 V. We can use this information to find the value of 1RC.
Using the formula:
V(1)=V0e−1/(RC)
Substituting the known values:
80=100e−1/(RC)
Dividing both sides by 100:
0.8=e−1/(RC)
Taking the natural logarithm of both sides:
ln(0.8)=−1RC
Thus,
1RC=−ln(0.8)
Step 2: Calculate the voltage after 2 seconds
Now we can find the voltage after 2 seconds using the same formula:
V(2)=V0e−2/(RC)
Substituting V0=100 V:
V(2)=100e−2/(RC)
We already have e−1/(RC)=0.8, so:
e−2/(RC)=(e−1/(RC))2=(0.8)2=0.64
Now substituting this back into the voltage equation:
V(2)=100×0.64=64V
Final Answer
The potential difference between the plates of the capacitor after 2 seconds is 64 V.
---
- V(t) is the voltage at time t,
- V0 is the initial voltage (100 V in this case),
- R is the resistance,
- C is the capacitance,
- t is the time.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT SECTION-D( LINKED COMPREHENSION TYPE QUESTIONS)
3 Videos
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT SECTION-D( LINKED COMPREHENSION TYPE QUESTIONS) Comprehension - II
5 Videos
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT SECTION-B(OBJECTIVE TYPE QUESTION ))
44 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COMMUNICATION SYSTEMS EXERCISE - ASSIGNMENT SECTION D (Assertion-Reason)
10 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
Similar Questions
The plates of a parallel plate capacitor are charged to a potential difference of 117 V and then connected across a resistor. The potential difference across the capacitor decreases exponentially with to time.After 1s the potential difference between the plates is 39 V, then after 2s from the start, the potential difference (in V) between the plates is
View SolutionFind charge on each capacitor and potential difference across each capacitor .

View Solution
Knowledge Check
A parallel plate air capacitor is charged to a potential difference of V volts. After disconnecting the charging battery the distance between the plates of the capacitor is increased using an isulating handle. As a result the potential difference between the plates
AincreasesBdecreaseCdoes not chargeDbecomes zero
A capacitor of capacity 2μF is charged to a potential difference of 12V. It is then connected across an inductor of inductance 6μH. At an instant when potential difference across the capacitor is 6V, what is the current(in A)?
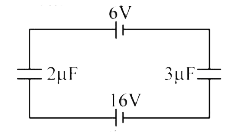
View SolutionWhat is the potential difference across 2μF capacitor in the circuit shown?
View SolutionA capacitor of capacitance C is charged to a potential difference V from a cell and then disconncted from it. A charge +Q is now given to its positive plate. The potential difference across the capacitor is now
View SolutionA capacitor of capacitance C is charged to a potential difference V from a cell and then disconncted from it. A charge +Q is now given to its positive plate. The potential difference across the capacitor is now
View SolutionA parallel plate air capacitor is charged to a potential difference of V volts. After disconnecting the charging battery the distance between the plates of the capacitor is increased using an isulating handle. As a result the potential difference between the plates
View SolutionA parallel plate air capacitor is charged to a potential difference of V volts. After disconnecting the charging battery the distance between the plates of the capacitor is increased using an isulating handle. As a result the potential difference between the plates
View SolutionA parallel plate capacitor is charged to a potential difference of 10 volts. After disconnecting the battery, distance between the plates of capacitor is decreased by using nonconducting handles. The potential difference between the plates will
View Solution
