A car travels half of the distance with constant velocity 100 km/h and another half with a constant velocity of 60 km/h along a straight line. The average velocity of the car is
The correct Answer is:75kmh−1
To find the average velocity of the car that travels half of the distance at a speed of 100 km/h and the other half at a speed of 60 km/h, we can follow these steps:
Step 1: Define the total distance
Let the total distance traveled by the car be D. Since the car travels half of the distance at each speed, we can denote the distance for each segment as:
- Distance for the first half: d=D2
- Distance for the second half: d=D2
Step 2: Calculate the time taken for each segment
- For the first half of the distance at 100 km/h:
t1=d100=D2100=D200
- For the second half of the distance at 60 km/h:
t2=d60=D260=D120
Step 3: Find the total time taken
The total time T taken to travel the entire distance is:
T=t1+t2=D200+D120
Step 4: Calculate the total time using LCM
To add the two fractions, we need to find the least common multiple (LCM) of the denominators 200 and 120. The LCM of 200 and 120 is 600. Therefore, we can rewrite the times as:
t1=D200=3D600
t2=D120=5D600
Now, adding these:
T=3D600+5D600=8D600=D75
Step 5: Calculate the average velocity
The average velocity V is given by the total distance divided by the total time:
V=DT=DD75=75 km/h
Conclusion
Thus, the average velocity of the car is 75 km/h.
---
Let the total distance traveled by the car be D. Since the car travels half of the distance at each speed, we can denote the distance for each segment as:
- Distance for the first half: d=D2
- Distance for the second half: d=D2
- For the first half of the distance at 100 km/h:
t1=d100=D2100=D200
t2=d60=D260=D120
The total time T taken to travel the entire distance is:
T=t1+t2=D200+D120
To add the two fractions, we need to find the least common multiple (LCM) of the denominators 200 and 120. The LCM of 200 and 120 is 600. Therefore, we can rewrite the times as:
t1=D200=3D600
t2=D120=5D600
T=3D600+5D600=8D600=D75
The average velocity V is given by the total distance divided by the total time:
V=DT=DD75=75 km/h
Thus, the average velocity of the car is 75 km/h.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - A)
58 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - B)
33 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - TRY YOURSELF
40 Videos
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -J (Aakash Challengers Questions)
7 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - J)
2 Videos
Similar Questions
A car travels half of the distance with constant velocity 40 km/h and another half with a constant velocity of 60 km/h along a straight line. The average velocity of the car is
View SolutionA car completes the first half of its journey with a velocity V1 and the remaining half with a velocity V2. Then the average velocity of the car for the whole journey is
View Solution
Knowledge Check
A man runs along the straight road for half the distance with velocity v1 and the remaining half distance with velocity v2. Then the average velocity is given by
Av1v2Bv22/v21C(v1+v2)/2D2v1v2/(v1+v2)
A car of mass 800 kg is moving with a constant velocity 40 km/h. Find the net force on it.
View SolutionA car of mass 800 kg is moving with a constant velocity 40 km/h . Find the net force on it.
View SolutionA car A moves along north with velocity 30 km/h and another car B moves along east with velocity 40 km/h. The relative velocity of A with respect to B is
View SolutionA person travels along a straight road for half the distance with velocity V1 and the remaining half distance with velocity V2 the average velocity is given by
View SolutionA car travels the first half of a distance between two places a speed of 30 km/hr and the second half of the distance a 50 km/hr. The average speed of the car for the whole journey is
View SolutionThe velocity-time graph of a car moving along a straight road is shown in figure. The average velocity of the car is first 25 seconds is
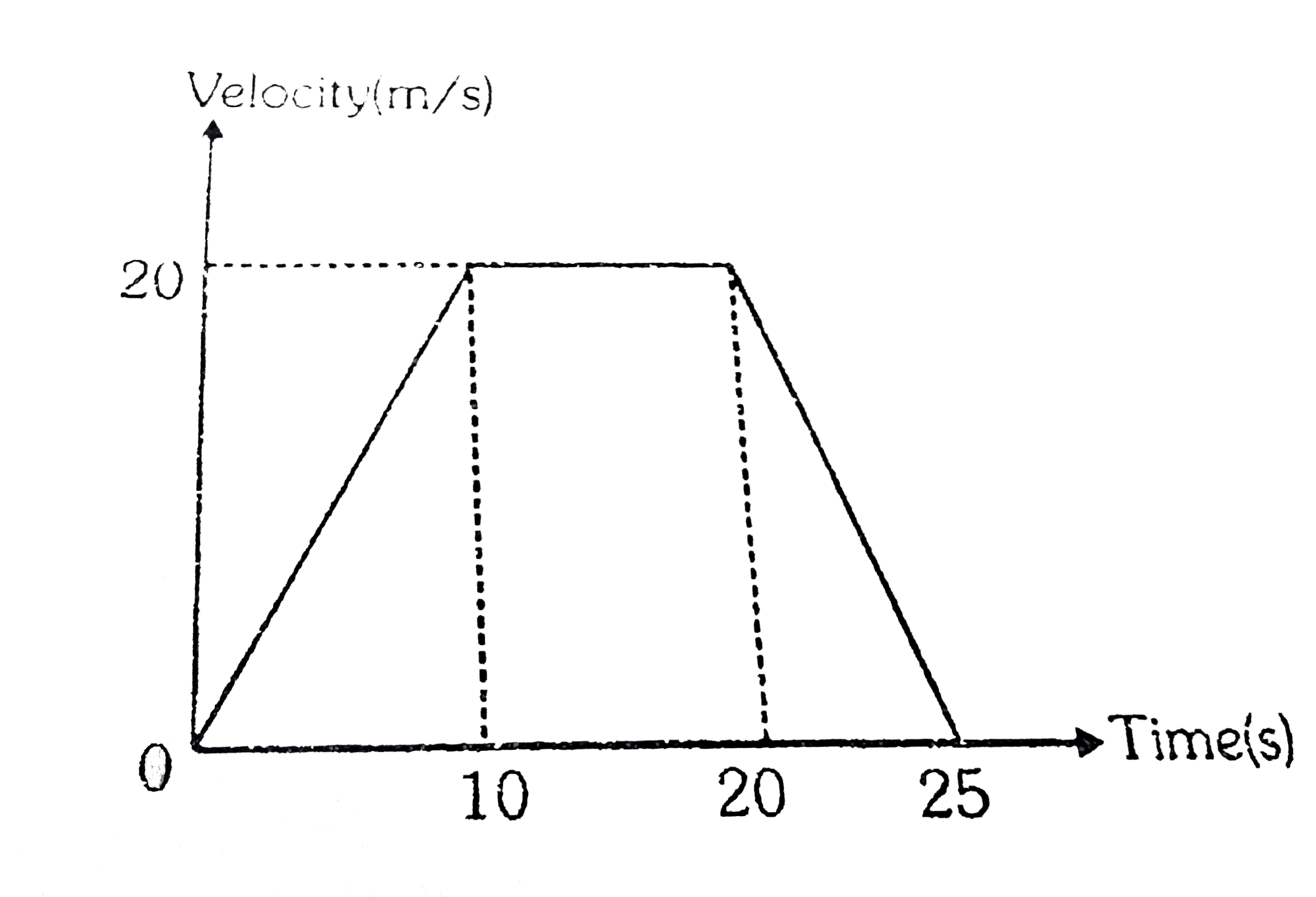
View SolutionThe velocity-time graph of a car moving along a straight road is shown in figure. The average velocity of the car in first 25 seconds is
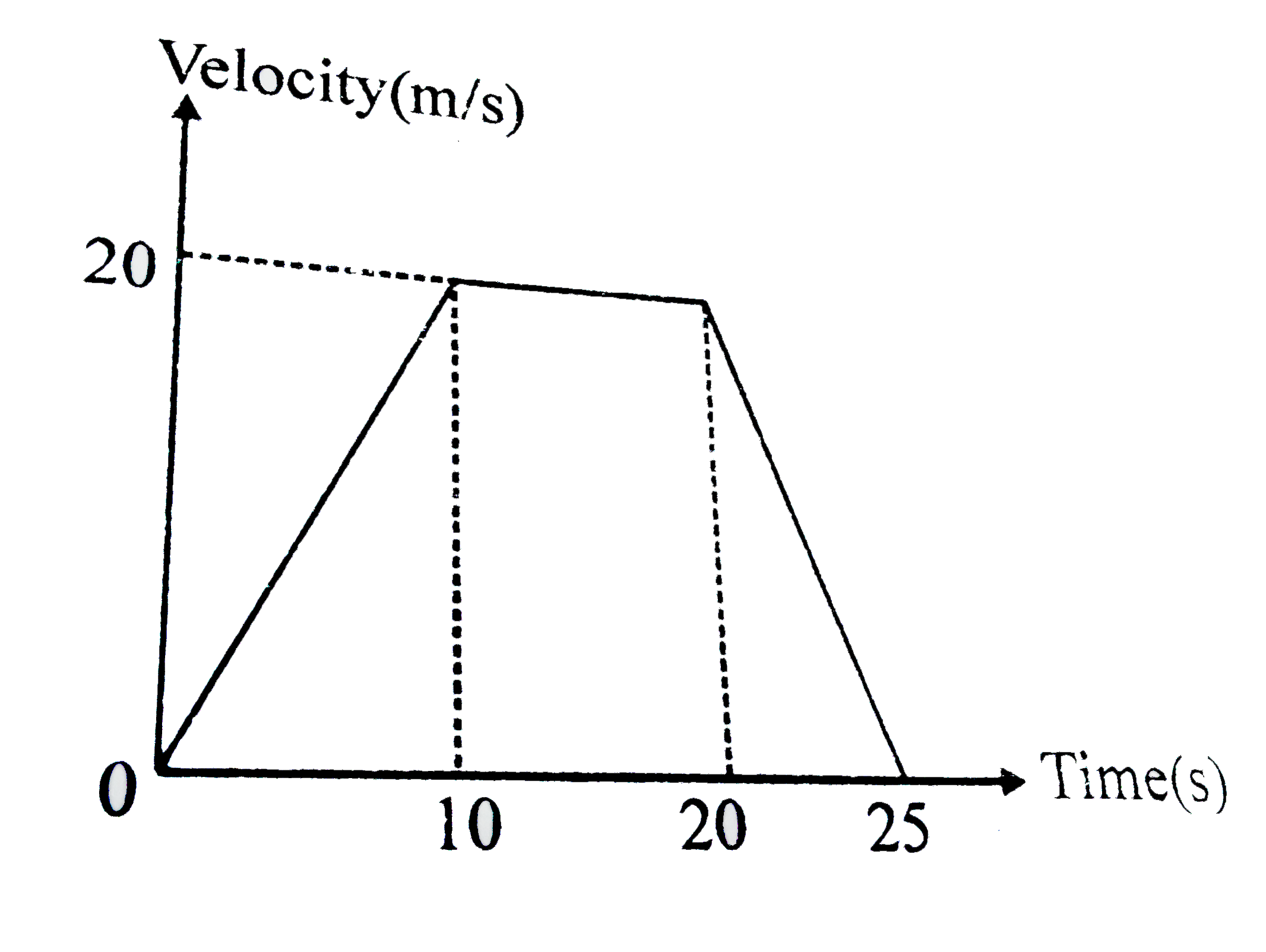
View Solution
