At any instant, the velocity and acceleration of a particle moving along a straight line are v and a. The speed of the particle is increasing if
v>0,a>0
v<0,a>0
v>0,a<0
v>0,a=0
The correct Answer is:A
To determine when the speed of a particle is increasing based on its velocity (v) and acceleration (a), we need to analyze the relationship between these two quantities.
1. Understanding Speed and Velocity:
- Speed is the magnitude of velocity. It is always a non-negative quantity.
- If the velocity is positive, the particle is moving in the positive direction; if negative, it's moving in the negative direction.
2. Role of Acceleration:
- Acceleration indicates how the velocity of an object is changing over time.
- If acceleration is positive, it means the velocity is increasing. If it is negative, the velocity is decreasing.
3. Condition for Increasing Speed:
- For the speed of the particle to increase, the velocity and acceleration must be in the same direction. This means:
- Both velocity (v) and acceleration (a) must be positive, or
- Both must be negative.
4. Analyzing the Options:
- Option 1: v is positive, a is positive.
- Here, both are positive, so the speed is increasing.
- Option 2: v is negative, a is positive.
- Here, velocity is negative and acceleration is positive, meaning the particle is slowing down (speed is decreasing).
- Option 3: v is positive, a is negative.
- Here, velocity is positive but acceleration is negative, meaning the particle is slowing down (speed is decreasing).
- Option 4: v is positive, a is 0.
- Here, the speed remains constant since acceleration is zero.
5. Conclusion:
- The only scenario where the speed of the particle is increasing is in Option 1, where both velocity and acceleration are positive.
Final Answer:
The speed of the particle is increasing if v is positive and a is positive (Option 1).
---
- Speed is the magnitude of velocity. It is always a non-negative quantity.
- If the velocity is positive, the particle is moving in the positive direction; if negative, it's moving in the negative direction.
- Acceleration indicates how the velocity of an object is changing over time.
- If acceleration is positive, it means the velocity is increasing. If it is negative, the velocity is decreasing.
- For the speed of the particle to increase, the velocity and acceleration must be in the same direction. This means:
- Both velocity (v) and acceleration (a) must be positive, or
- Both must be negative.
- Option 1: v is positive, a is positive.
- Here, both are positive, so the speed is increasing.
- Option 2: v is negative, a is positive.
- Here, velocity is negative and acceleration is positive, meaning the particle is slowing down (speed is decreasing).
- Option 3: v is positive, a is negative.
- Here, velocity is positive but acceleration is negative, meaning the particle is slowing down (speed is decreasing).
- Option 4: v is positive, a is 0.
- Here, the speed remains constant since acceleration is zero.
- The only scenario where the speed of the particle is increasing is in Option 1, where both velocity and acceleration are positive.
The speed of the particle is increasing if v is positive and a is positive (Option 1).
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - B)
33 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - C)
36 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - EXERCISE
29 Videos
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -J (Aakash Challengers Questions)
7 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - J)
2 Videos
Similar Questions
If a particle is moving along straight line with increasing speed, then
View SolutionThe velocity –position graph of a particle moving along a straight line is shown. Then acceleration of the particle at s = 15 m is :

View SolutionThe x-t graph of a particle moving along a straight line is shown in figure

The speed-time graph of the particle is correctly shown by
View SolutionLet v and a be the instantaneous velocity and acceleration of a particle moving in a plane. Then rate of change of speed dvdt of the particle is equal to
View SolutionThe variation of velocity of a particle moving along a straight line is shown in . is
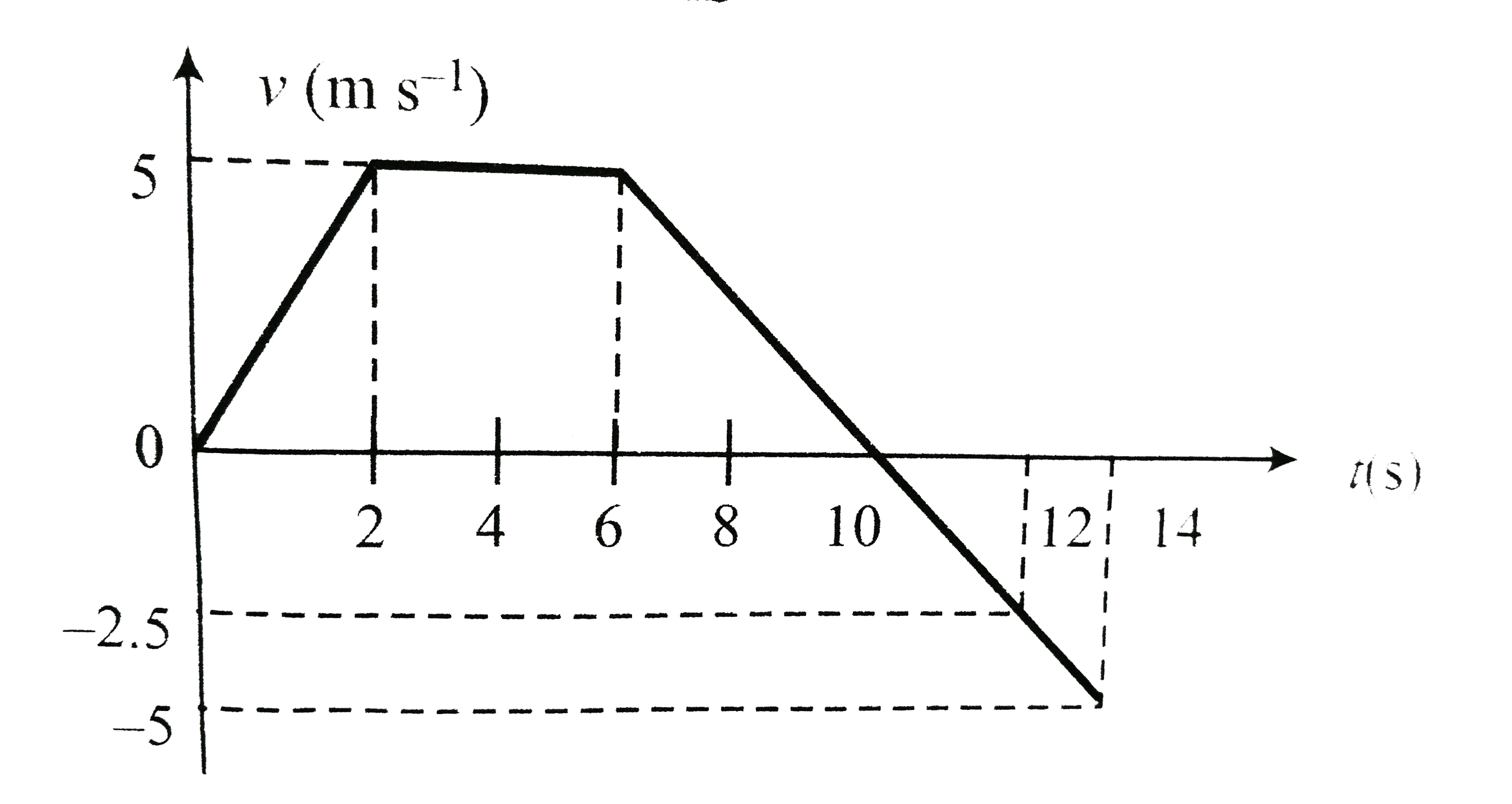 .
.
View SolutionThe x-t graph of a particle moving along a straight line is shown in figure
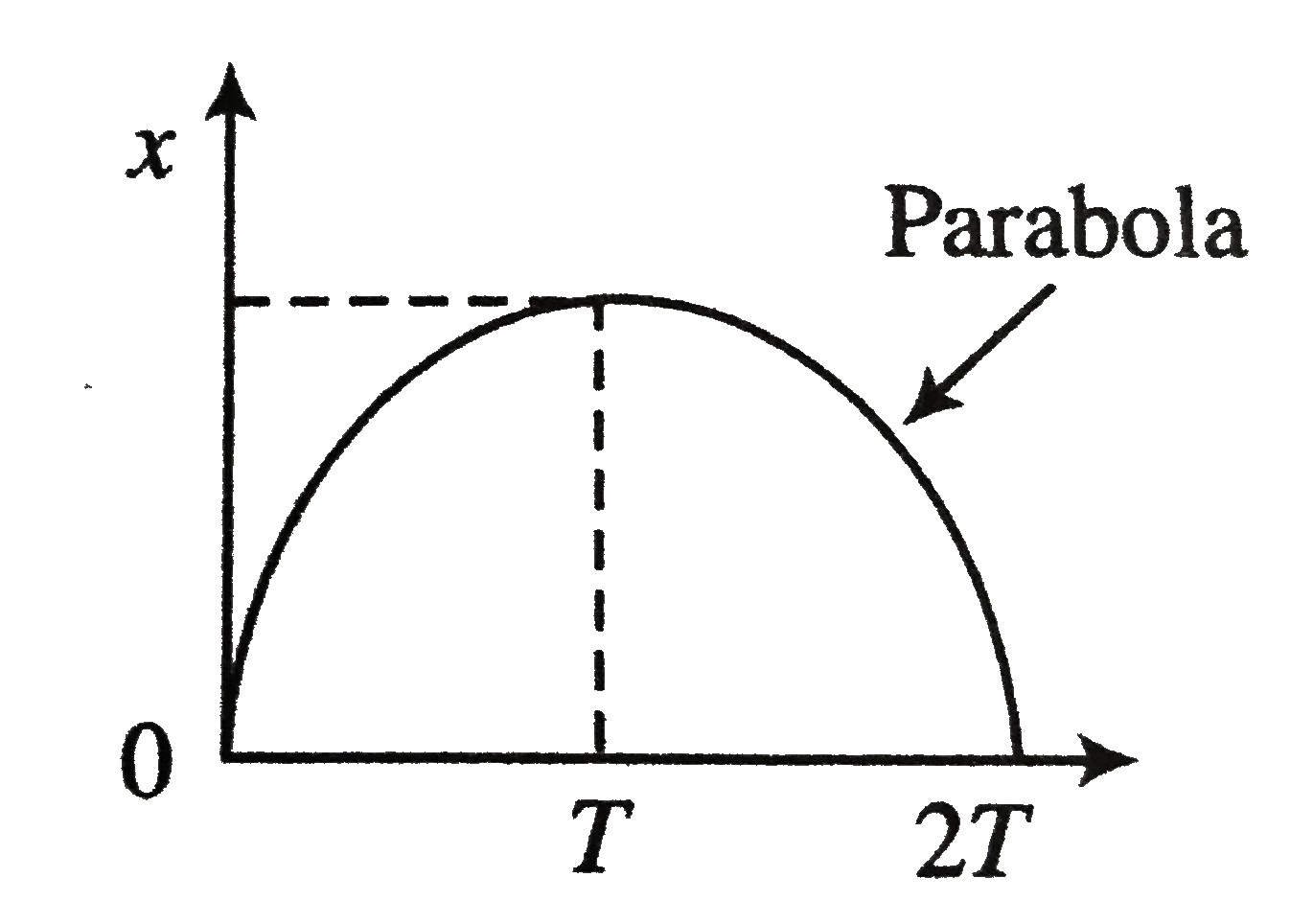
The v-t graph of the particle is correctly shown by
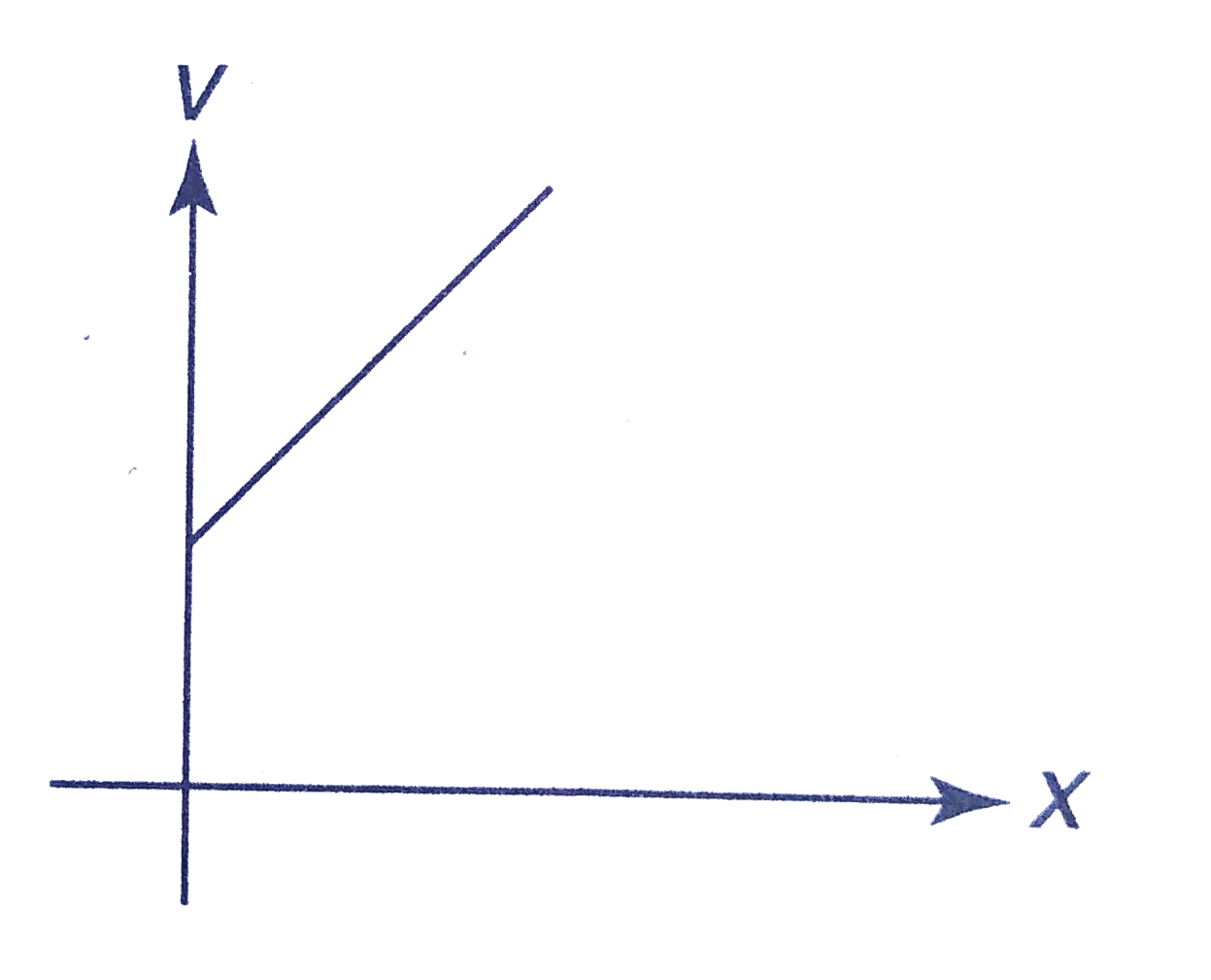
View Solution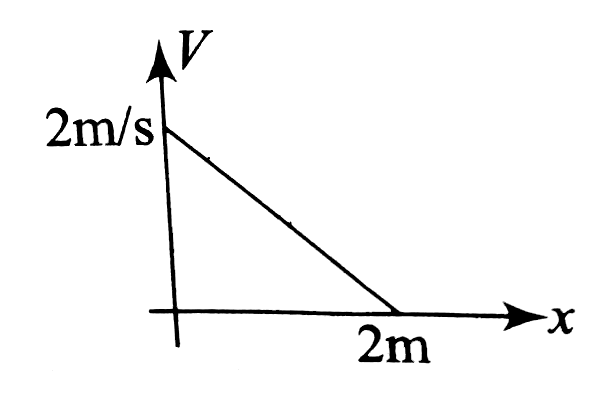
The velocity displacement graph of a particle moving along a straight line is shown in figure.
Then the acceleration displacement graph is.
View SolutionGraph of velocity versus displacement of a particle moving in a straight line is as shown in figure.
The acceleration of the particle is.
View SolutionThe acceleration of a particle starting from rest and travelling along a straight line is shown in figure. The maximum speed of the particle is
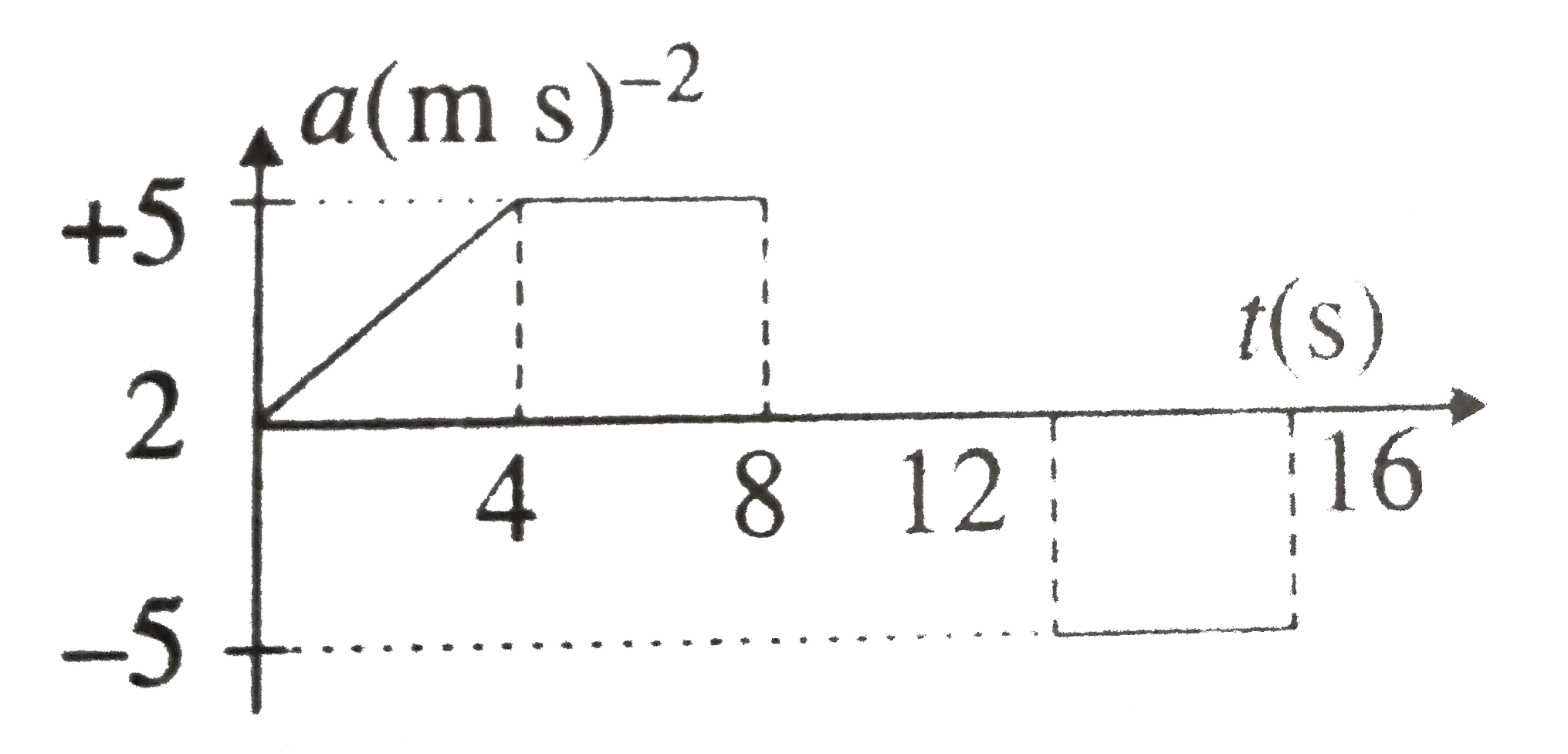
View SolutionThe variation of velocity of a particle moving along a straight line is shown in the figure. The distance travelled by the particle in 4s is
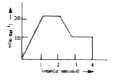
View Solution
