If the velocity of a particle is v=At+Bt2, where A and B are constants, then the distance travelled by it between 1s and 2s is
A2+B3
32A+4B
3A+7B
32A+73B
The correct Answer is:D
Step by step video & image solution for If the velocity of a particle is v = At+Bt^(2), where A and B are constants, then the distance travelled by it between 1s and 2s is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - B)
33 Videos
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -J (Aakash Challengers Questions)
7 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - J)
2 Videos
Similar Questions
If the velocity of a particle is v=At+Bt2, where A and B are constant, then the distance travelled by it between 1s and 2s is :
View SolutionIf the velocity of a particle is v=At+Bt2, where A and B are constant, then the distance travelled by it between 1s and 2s is :
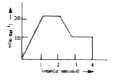
View SolutionThe variation of velocity of a particle moving along a straight line is shown in the figure. The distance travelled by the particle in 4s is
View SolutionThe position of a particle is given by
x=2(t−t2)
where t is expressed in seconds and x is in metre.
The total distance travelled by the paticle between t=0 to t=1s is
View SolutionThe position (in meters) of a particle moving on the x-axis is given by: x=2+9t+3t2−t3, where t is time in seconds . The distance travelled by the particle between t= 1s and t= 4s is m.
View SolutionIf xy=a2andS=b2x+c2y where a,bandc are constants then the minimum value of S is
View SolutionThe momentum of a particle is P=A+Bt2 . Where , A and B are constant perpendicular vectors . The force acting on the particle when its acceleration is at 45∘ with its velocity is
(a)2√ABB (b)2B (c)zero (d)2A
View SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The distance travelled by particle from t=0 to t=2seconds is :
View SolutionLet the instantaneous velocity of a rocket, just after launching, be given by the expression v=2t+3t2 (where v is in ms−1 and t is in seconds). Find out the distance travelled by the rocket from t=2s to t=3s.
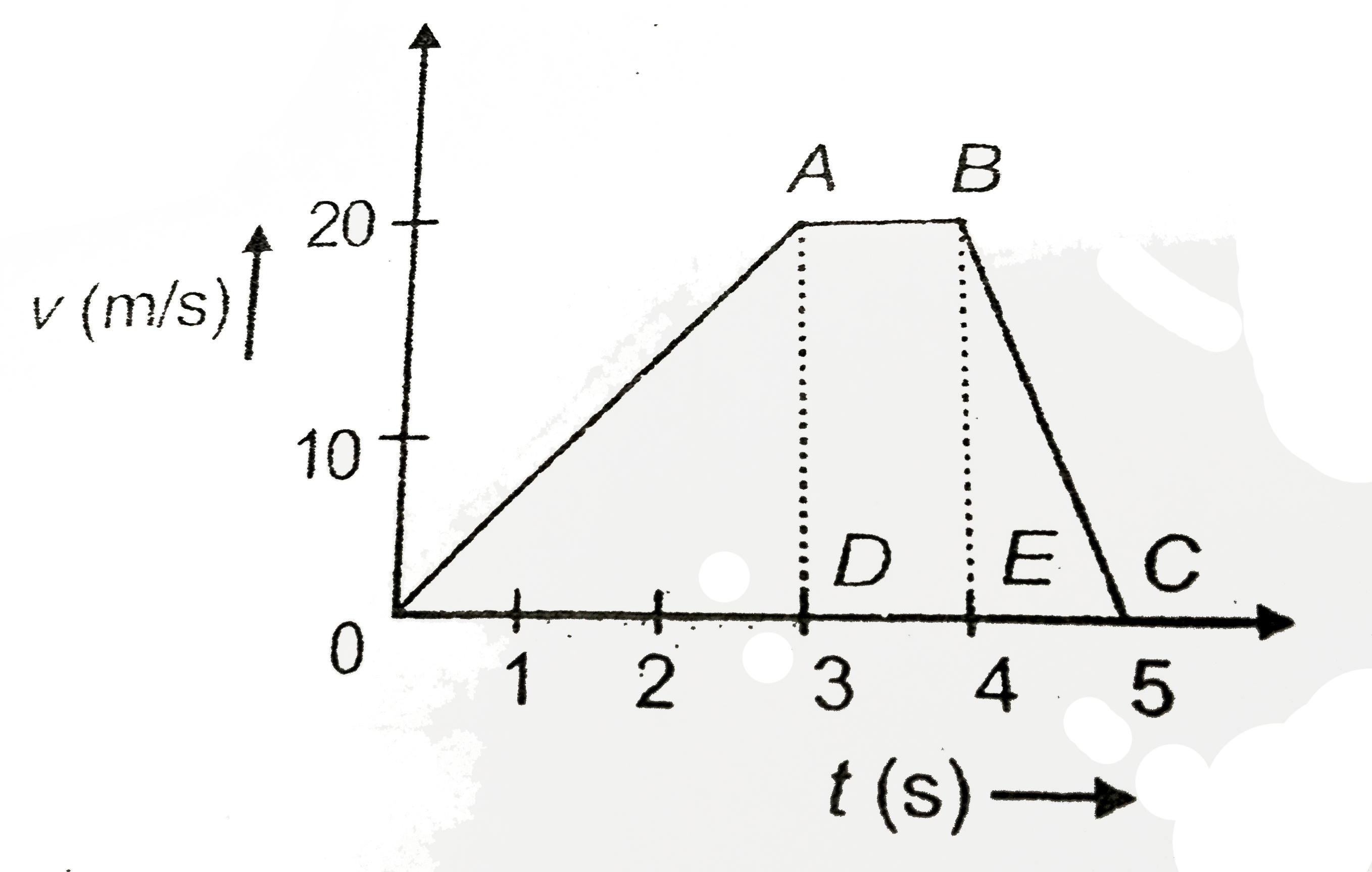
View SolutionThe variation of velocity of a particle moving along a straight line is as shown in the figure given below. The distance travelled by the particle in 5 s is
View Solution