A particle moves in a straight line with a constant acceleration. Its velocity changes from 20ms−1 to 35ms−1 while passing through a distance 150m in t seconds. The value of t is.
To solve the problem step by step, we will use the equations of motion under constant acceleration.
Step 1: Identify the known values
- Initial velocity (u) = 20 m/s
- Final velocity (v) = 35 m/s
- Distance (s) = 150 m
Step 2: Use the equation to find acceleration
We can use the equation of motion:
v2−u2=2as
Where:
- a is the acceleration.
Rearranging the formula to solve for acceleration a:
a=v2−u22s
Step 3: Substitute the known values into the equation
Substituting the values into the equation:
a=(35)2−(20)22×150
Step 4: Calculate the acceleration
Calculating the squares:
a=1225−400300
a=825300
a=2.75m/s2
Step 5: Use the acceleration to find time (t)
Now we can use the formula:
v=u+at
Rearranging the formula to solve for time t:
t=v−ua
Step 6: Substitute the known values into the equation for time
Substituting the values:
t=35−202.75
Step 7: Calculate the time
Calculating the difference:
t=152.75
t≈5.45seconds
Final Answer
The value of t is approximately 5.45 seconds.
---
- Initial velocity (u) = 20 m/s
- Final velocity (v) = 35 m/s
- Distance (s) = 150 m
We can use the equation of motion:
v2−u2=2as
Where:
- a is the acceleration.
a=v2−u22s
Substituting the values into the equation:
a=(35)2−(20)22×150
Calculating the squares:
a=1225−400300
a=825300
a=2.75m/s2
Now we can use the formula:
v=u+at
Rearranging the formula to solve for time t:
t=v−ua
Substituting the values:
t=35−202.75
Calculating the difference:
t=152.75
t≈5.45seconds
The value of t is approximately 5.45 seconds.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBook:AAKASH INSTITUTE ENGLISHChapter:MOTION IN A STRAIGHT LINEExercise:ASSIGNMENT (SECTION - D)
Explore 15 Videos
- MOTION IN A STRAIGHT LINEBook:AAKASH INSTITUTE ENGLISHChapter:MOTION IN A STRAIGHT LINEExercise:ASSIGNMENT (SECTION - B)
Explore 33 Videos
- MOTION IN A PLANEBook:AAKASH INSTITUTE ENGLISHChapter:MOTION IN A PLANEExercise:Assignement section -J (Aakash Challengers Questions)
Explore 7 Videos
- MOTION IN STRAIGHT LINEBook:AAKASH INSTITUTE ENGLISHChapter:MOTION IN STRAIGHT LINEExercise:Assignment (SECTION - J)
Explore 2 Videos
Similar Questions
A particle moves in a straight line with a constant acceleration. It changes its velocity from 10ms−1 to 20ms−1 while passing through a distance 135m in t seconds. The value of t is.
(a) 10 (b) 1.8 (c) 12 (d) 9
View SolutionAverage velocity of a particle moving in a straight line, with constant acceleration a and initial velocity u in first t seconds is.
View SolutionAverage velocity of a particle moving in a straight line, with constant acceleration a and initial velocity u in first t seconds is.
View SolutionA particle moves in straight line. Acceleration of particle changes with velocity as showns in graph:

View SolutionA particle is moving along a straight line with constant acceleration. At the end of tenth second its velocity becomes 20m/s and tenth second it travels a distance od 10m. Then the acceleration of the particle will be.
View SolutionA particle starts from rest at t=0 and moves in a straight line with an acceleration as shown below. The velocity of the particle at t=3 s is

View SolutionA particle moving along a straight line with a constant acceleration of −4m/s2 passes through a point A on the line with a velocity of +8m/s at some moment. Find the distance travelled by the particle in 5 seconds after that moment.
View SolutionA particle moving along a straight line with a constant acceleration of −4m/s2 passes through a point A on the line with a velocity of +8m/s at some moment. Find the distance travelled by the particle in 5 seconds after that moment.
View SolutionA particle moves in a circle of radius 4 m with a linear velocity of 20ms−1. Find the angular velocity.
View SolutionIf the velocity v of particle moving along a straight line decreases linearly with its displacement s from 20ms−1 to a value approaching zero at s = 30 m, then acceleration of the particle at v=10ms^(-1) is
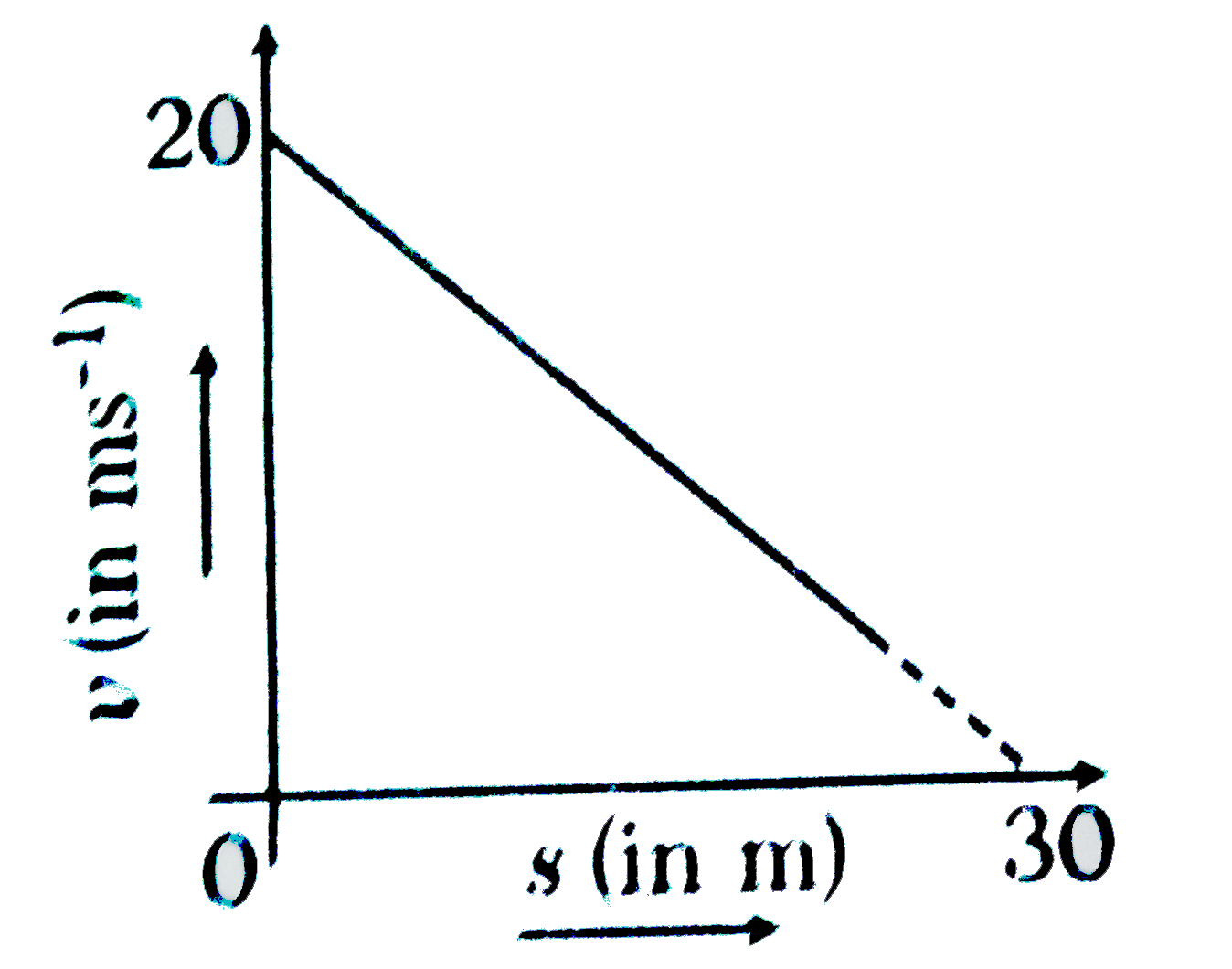
View Solution
