A particle moves in a straight line with a constant acceleration. It changes its velocity from to while passing through a distance in seconds. The value of is.
(a) 10
(b) 1.8
(c) 12
(d) 9
10
1.8
12
9
The correct Answer is:D
To solve the problem, we will use the equations of motion for a particle moving with constant acceleration. We are given the initial velocity (u), final velocity (v), distance (s), and we need to find the time (t).
1. Identify the given values:
- Initial velocity, u=10m/s
- Final velocity, v=20m/s
- Distance, s=135m
2. Use the third equation of motion to find acceleration (a):
The third equation of motion states:
v2=u2+2as
Substituting the known values:
(20)2=(10)2+2a(135)
This simplifies to:
400=100+270a
Rearranging gives:
400−100=270a⟹300=270a⟹a=300270=109m/s2
3. Use the first equation of motion to find time (t):
The first equation of motion states:
v=u+at
Substituting the known values:
20=10+(109)t
Rearranging gives:
20−10=109t⟹10=109t
To isolate t, multiply both sides by 910:
t=10⋅910=9s
4. Final Answer:
The value of t is 9s.
- Initial velocity, u=10m/s
- Final velocity, v=20m/s
- Distance, s=135m
The third equation of motion states:
v2=u2+2as
Substituting the known values:
(20)2=(10)2+2a(135)
This simplifies to:
400=100+270a
Rearranging gives:
400−100=270a⟹300=270a⟹a=300270=109m/s2
The first equation of motion states:
v=u+at
Substituting the known values:
20=10+(109)t
Rearranging gives:
20−10=109t⟹10=109t
To isolate t, multiply both sides by 910:
t=10⋅910=9s
The value of t is 9s.
Similar Questions
A particle moves in a straight line with a constant acceleration. Its velocity changes from 20ms−1 to 35ms−1 while passing through a distance 150m in t seconds. The value of t is.
View SolutionAverage velocity of a particle moving in a straight line, with constant acceleration a and initial velocity u in first t seconds is.
View SolutionAverage velocity of a particle moving in a straight line, with constant acceleration a and initial velocity u in first t seconds is.
View SolutionA particle is moving along a straight line with constant acceleration. At the end of tenth second its velocity becomes 20m/s and tenth second it travels a distance od 10m. Then the acceleration of the particle will be.
View SolutionA particle moves in a straight line such that its distance in 't' seconds from a fixed point is (6t−t2) cm. find its velocity at the end of t=2 sec.
View SolutionThe velocity-time graph of a particle moving along a straight line is shown is . The rate of acceleration and deceleration is constant and it is equal to 5ms−2. If the a average velocity during the motion is 20ms−1, Then
 .
.
The value of t is.
View SolutionA particle starts to move in a straight line from a point with velocity 10 m s−1 and acceleration - 2.0 ms−2. Find the position and velocity of the particle at (i) t = 5 s, (ii) t' = 10 s.
View SolutionA particle starting from rest moves in a straight line with acceleration as shown in the a-t graph. Find the distance (in m) travelled by the particle in the first four seconds from start of its motion.
Q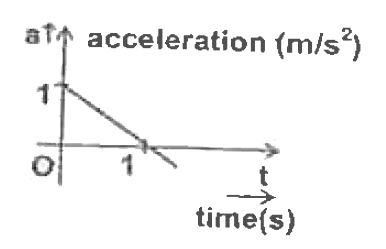
View SolutionA particle is moving in a straight line as :
a=1m/s20≤t≤10
a=2tt>10
where t is the time and a is the acceleration. If initial velocity of the particla is zero then :
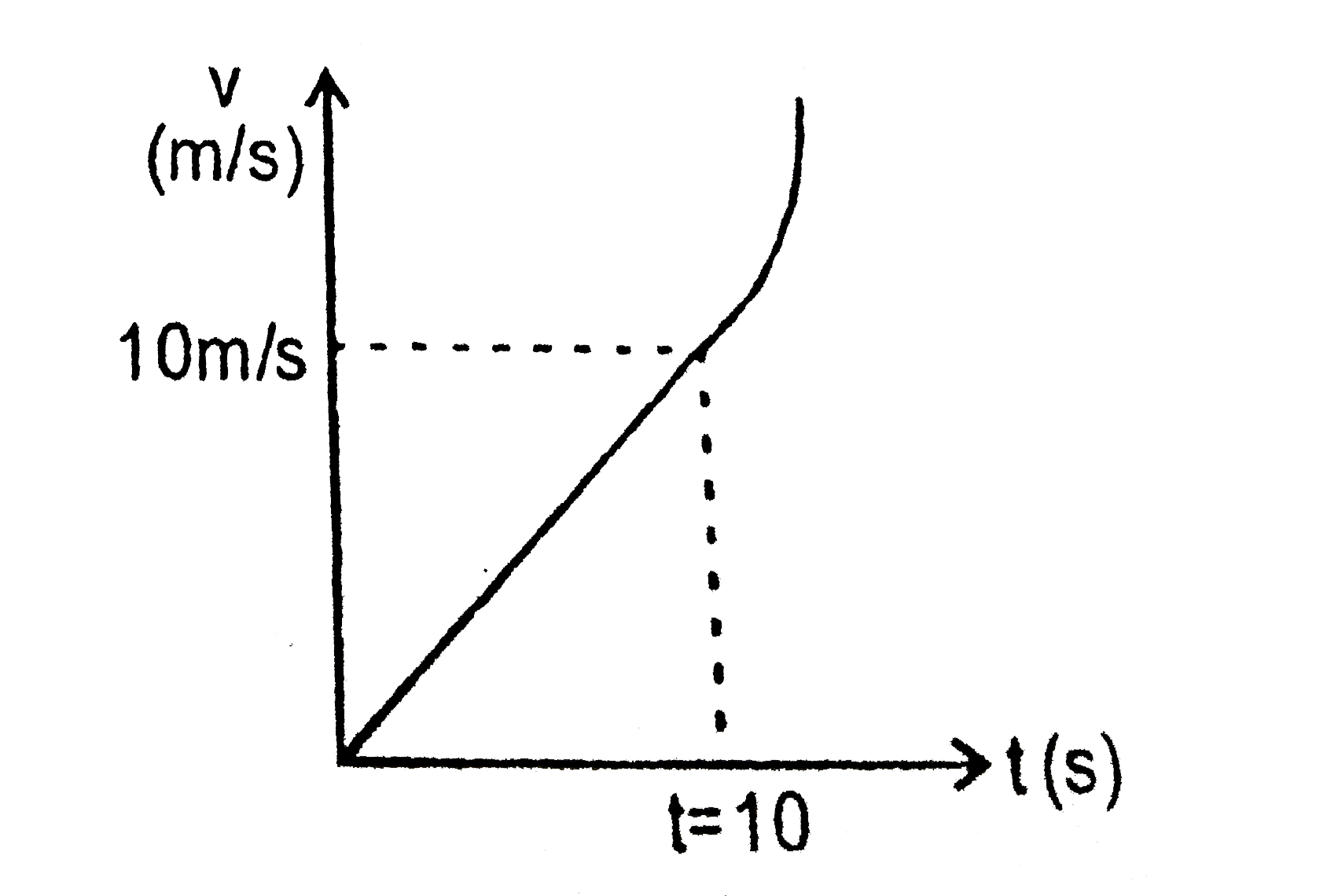
View SolutionA particle is moving on a straight line. Its velocity at time t is (8−2t)m/s. What is the total distance covered from t=0 to t=6s?
View Solution
