A particle is in uniform circular motion, then its velocity is perpendicular to
Net force
Centripetal acceleration
Angular velocity
All of these
To solve the question, "A particle is in uniform circular motion, then its velocity is perpendicular to," we need to analyze the motion of the particle in a circular path. Here is the step-by-step solution:
Step 1: Understand Uniform Circular Motion
In uniform circular motion, a particle moves in a circular path with a constant speed. This means that while the speed (magnitude of velocity) remains constant, the direction of the velocity changes continuously.
Hint: Remember that in uniform circular motion, the speed is constant, but the direction of velocity changes.
Step 2: Identify the Direction of Velocity
The velocity of the particle in circular motion is always tangent to the circular path at any point. This tangential direction means that the velocity vector is perpendicular to the radius drawn from the center of the circle to the particle.
Hint: Visualize the circular path and note that the tangent at any point is the direction of velocity.
Step 3: Analyze the Acceleration
In uniform circular motion, there is a centripetal acceleration acting on the particle, directed towards the center of the circle. This acceleration is responsible for changing the direction of the velocity vector, keeping the particle in circular motion.
Hint: Recall that centripetal acceleration is always directed towards the center of the circle.
Step 4: Determine the Relationship Between Velocity and Acceleration
Since the velocity is tangential to the circle and the acceleration (centripetal acceleration) is directed radially inward, we can conclude that the velocity vector is perpendicular to the acceleration vector.
Hint: Use the concept of perpendicular vectors; if one vector points tangentially and the other radially, they are perpendicular.
Step 5: Conclusion
Based on the analysis, we can conclude that in uniform circular motion, the velocity of the particle is perpendicular to the radius of the circle, the acceleration, and the net force acting on the particle.
Final Answer: The velocity of a particle in uniform circular motion is perpendicular to the radius of the circle, the centripetal acceleration, and the net force acting on it.
In uniform circular motion, a particle moves in a circular path with a constant speed. This means that while the speed (magnitude of velocity) remains constant, the direction of the velocity changes continuously.
The velocity of the particle in circular motion is always tangent to the circular path at any point. This tangential direction means that the velocity vector is perpendicular to the radius drawn from the center of the circle to the particle.
In uniform circular motion, there is a centripetal acceleration acting on the particle, directed towards the center of the circle. This acceleration is responsible for changing the direction of the velocity vector, keeping the particle in circular motion.
Since the velocity is tangential to the circle and the acceleration (centripetal acceleration) is directed radially inward, we can conclude that the velocity vector is perpendicular to the acceleration vector.
Based on the analysis, we can conclude that in uniform circular motion, the velocity of the particle is perpendicular to the radius of the circle, the acceleration, and the net force acting on the particle.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-A)
65 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-B)
44 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Example
24 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
Similar Questions
Knowledge Check
For a particle performing uniform circular motion, choose the incorrect statement form the following.
AMagnitude of particle velocity (speed) remains constant.BParticle velocity remains directed perpendicular to radius vector.CDirection of acceleration keeps changing as particle moves.DMagnitudes of acceleration does not remain constant.
Uniform circular motion is an example of
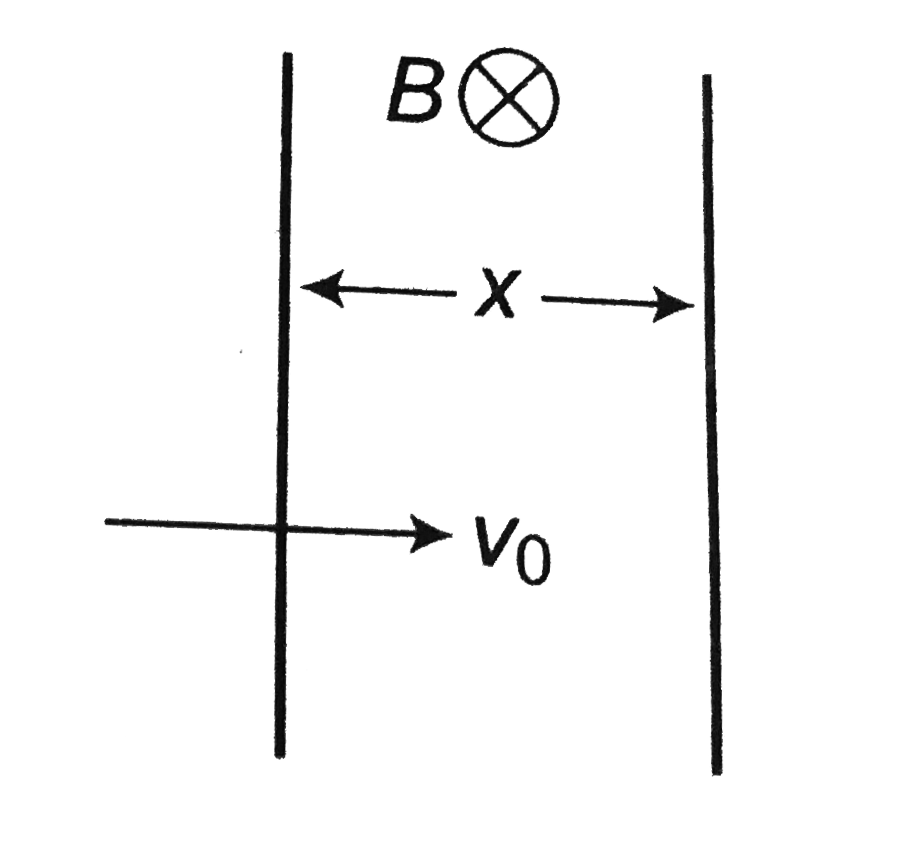
View SolutionA charged particle enters into a uniform magnetic field with velocity v0 perpendicular to it , the length of magnetic field is x=√32R, where R is the radius of the circular path of the particle in the field .The magnitude of charge in velocity of the particle when it comes out of the field is
View SolutionDuring uniform circular motion of a particle
View SolutionIs a body in uniform circular motion in equilibrium ?
View SolutionThe acceleration vector of a particle in uniform circular motion averaged over the cycle is a null vector. This statement is
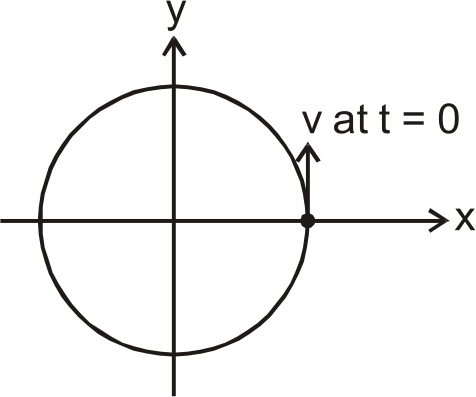
View SolutionA particle is moving in a uniform circular motion on a horizontal surface. Particle's position and velocity at time t = 0 are shown in the figure in the coordinate system. Which of the indicated variable on the vertical axis is/are correctly matched by the graph(s) shown alongside for particle's motion ?
View SolutionIn case of a uniform circular motion, velocity and acceleration are
View Solution
