Two blocks of masses 2 kg and 4 kg are hanging with the help of massless string passing over an ideal pulley inside an elevator. The elevator is moving upward with an acceleration g2. The tension in the string connected between the blocks will be (Take g=10m/s2).
40 N
60 N
80 N
20 N
To solve the problem, we need to find the tension in the string connecting two blocks of masses 2 kg and 4 kg, which are hanging inside an elevator that is accelerating upward with an acceleration of g2. We will take g=10m/s2.
1. Identify the Effective Acceleration:
The elevator is moving upward with an acceleration of g2. Thus, the effective acceleration acting on the blocks can be calculated as:
geffective=g+g2=g+5=10+5=15m/s2
2. Set Up the Forces:
- For the 4 kg block (let's call it Block A):
- Weight WA=mA⋅geffective=4⋅15=60N (acting downward)
- Tension T (acting upward)
- For the 2 kg block (let's call it Block B):
- Weight WB=mB⋅geffective=2⋅15=30N (acting downward)
- Tension T (acting upward)
3. Write the Equations of Motion:
- For Block A (4 kg):
T−WA=−mA⋅a(moving down)
T−60=−4a(1)
- For Block B (2 kg):
T−WB=mB⋅a(moving up)
T−30=2a(2)
4. Express Acceleration:
Since the blocks are connected by a string, the acceleration a of both blocks is the same. We can express a from equation (2):
a=T−302(3)
5. Substitute Acceleration into Equation (1):
Substitute a from equation (3) into equation (1):
T−60=−4(T−302)
Simplifying this gives:
T−60=−2(T−30)
T−60=−2T+60
T+2T=60+60
3T=120
T=40N
Final Answer:
The tension in the string connected between the blocks is T=40N.
---
The elevator is moving upward with an acceleration of g2. Thus, the effective acceleration acting on the blocks can be calculated as:
geffective=g+g2=g+5=10+5=15m/s2
- For the 4 kg block (let's call it Block A):
- Weight WA=mA⋅geffective=4⋅15=60N (acting downward)
- Tension T (acting upward)
- For the 2 kg block (let's call it Block B):
- Weight WB=mB⋅geffective=2⋅15=30N (acting downward)
- Tension T (acting upward)
- For Block A (4 kg):
T−WA=−mA⋅a(moving down)
T−60=−4a(1)
- For Block B (2 kg):
T−WB=mB⋅a(moving up)
T−30=2a(2)
Since the blocks are connected by a string, the acceleration a of both blocks is the same. We can express a from equation (2):
a=T−302(3)
Substitute a from equation (3) into equation (1):
T−60=−4(T−302)
Simplifying this gives:
T−60=−2(T−30)
T−60=−2T+60
T+2T=60+60
3T=120
T=40N
The tension in the string connected between the blocks is T=40N.
Topper's Solved these Questions
- LAWS OF MOTIONBook:AAKASH INSTITUTE ENGLISHChapter:LAWS OF MOTIONExercise:Assignment (SECTION-A)
Explore 65 Videos
- LAWS OF MOTIONBook:AAKASH INSTITUTE ENGLISHChapter:LAWS OF MOTIONExercise:Assignment (SECTION-B)
Explore 44 Videos
- LAWS OF MOTIONBook:AAKASH INSTITUTE ENGLISHChapter:LAWS OF MOTIONExercise:Example
Explore 24 Videos
- KINETIC THEORYBook:AAKASH INSTITUTE ENGLISHChapter:KINETIC THEORYExercise:EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
Explore 10 Videos
- MAGNETISM AND MATTER Book:AAKASH INSTITUTE ENGLISHChapter:MAGNETISM AND MATTER Exercise:ASSIGNMENT (SECTION D)
Explore 26 Videos
Similar Questions
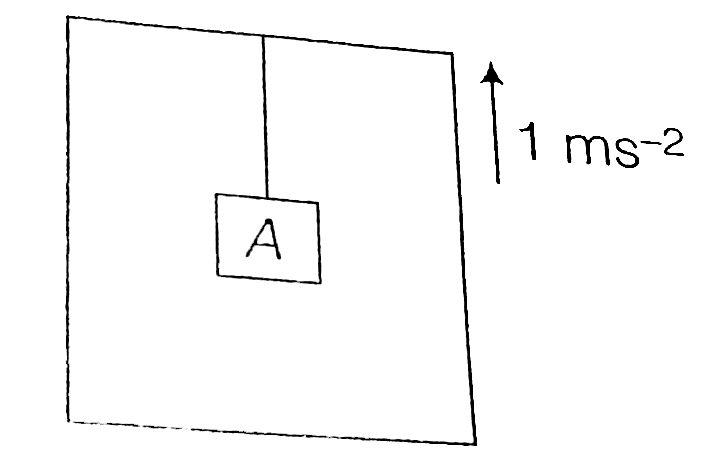
If the elevator in shown figure is moving upwards with constant acceleration 1ms−2, tension in the string connected to block A of mass 6 kg would be ( take, g=10ms−2)
View SolutionTwo bodies of masses m1 and m2 are connected a light string which passes over a frictionless massless pulley. If the pulley is moving upward with uniform acceleration g2, then tension in the string will be
View Solution
Knowledge Check
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A lift of mass 100 kg is moving upwards with an acceleration of 1 m/s2. The tension developed in the string, which is connected to lift is (g=9.8m/s2)
View SolutionTwo bodies of masses 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a frictionless pulley. The acceleration of the system is :
View SolutionTwo blocks of masses 6kg and 4kg are attached to the two ends of a massless string passing over a smooth fixed pulley. if the system is released, the acceleration of the centre of mass of the system will be
View SolutionTwo masses 2 kg and 4 kg are connected at the two ends of light inextensible string passing over a frictionless pulley. If the masses are released, then find the acceleration of the masses and the tension in the string.
View SolutionA lift of mass 200 kg is moving upward with an acceleration of 3m/s2 . If g=10m/s2 then the tension of string of the lift will be :
View SolutionTwo masses 2 kg and 4 kg are connected at two ends of light inextensible string passing over a frictionless pulley . If the masses are released , then find the accelaration of the masses and the tension in the string .
View SolutionA block of mass 5kg is hung with the help of light string which is passing over an ideal pulley as shown as in figure.The force is exerted by the clamp on the pulley will be (g= 10 m/s^2)
_PHY_E05_165_Q01.png)
View Solution