A weight mg is suspended from the middle of a rope whose ends are at the same level. The rope is no longer horizontal. Find the minimum tenstion required to completely straighten the rope.
Mg2
Mgcosθ
2Mgcosθ
Infinitely large
To solve the problem of finding the minimum tension required to completely straighten the rope from which a weight mg is suspended, we can follow these steps:
Step 1: Understand the Setup
We have a rope suspended from a ceiling with a weight mg attached at its midpoint. The ends of the rope are at the same level, and when the weight is attached, the rope forms an angle θ with the horizontal.
Step 2: Analyze Forces Acting on the Weight
When the weight is hanging, the tension T in the rope has two components:
- The vertical component: Tcosθ
- The horizontal component: Tsinθ
Since the rope is symmetrical, the vertical components from both sides of the rope will balance the weight.
Step 3: Set Up the Equation for Vertical Forces
The total upward force due to tension must balance the downward force due to the weight:
2Tcosθ=mg
From this equation, we can express the tension T in terms of mg and θ:
T=mg2cosθ
Step 4: Consider the Condition for Straightening the Rope
To completely straighten the rope, the angle θ must become 90∘. At this angle:
cos90∘=0
Substituting θ=90∘ into the tension equation gives:
T=mg2cos90∘=mg2⋅0
This results in division by zero.
Step 5: Conclusion
Since dividing by zero is undefined, it implies that an infinite amount of tension would be required to completely straighten the rope. Therefore, the minimum tension required to straighten the rope is infinite.
Final Answer
The minimum tension required to completely straighten the rope is infinite.
---
We have a rope suspended from a ceiling with a weight mg attached at its midpoint. The ends of the rope are at the same level, and when the weight is attached, the rope forms an angle θ with the horizontal.
When the weight is hanging, the tension T in the rope has two components:
- The vertical component: Tcosθ
- The horizontal component: Tsinθ
The total upward force due to tension must balance the downward force due to the weight:
2Tcosθ=mg
From this equation, we can express the tension T in terms of mg and θ:
T=mg2cosθ
To completely straighten the rope, the angle θ must become 90∘. At this angle:
cos90∘=0
Substituting θ=90∘ into the tension equation gives:
T=mg2cos90∘=mg2⋅0
This results in division by zero.
Since dividing by zero is undefined, it implies that an infinite amount of tension would be required to completely straighten the rope. Therefore, the minimum tension required to straighten the rope is infinite.
The minimum tension required to completely straighten the rope is infinite.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-B)
44 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-C)
63 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE
69 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
Similar Questions

A block of mass m is suspended from one end of a light spring as shown. The origin O is considered at distance equal to natural length of the spring from the ceiling and vertical downwards direction as positive y-axis. When the system is in equilibrium a bullet of mass m3 moving in vertical up wards direction with velocity v0 strikes the block and embeds into it. As a result, the block (with bullet embedded into it) moves up and start oscillating. Based on the given information, answer the following question:
Q. The time taken by the block bullet system to move from y=mgk (initial equilibrium position) to y=0 (natural length of spring) is (A represents the amplitude of motion)
View SolutionA weight w is suspended from the midpoint of a rope, whose ends are at the same level. In order to make the rope perfectly horizontal, the force applied to each of its ends must be
View SolutionA weight w is suspended from the midpoint of a rope, whose ends are at the same level. In order to make the rope perfectly horizontal, the force applied to each of its ends must be
View SolutionTwo persons are holding a rope of negligible weight tightly at its ends so that it is horizontal. A 15kg weight is attached to the mid point which is no longer remains horizontal. The minimum tension required to completely straighten the rope is:
View SolutionA heavy rope is suspended from a rigid support A wave pulse is set up at the lower end, then
View SolutionA heavy rope is suspended from a rigid support A wave pulse is set up at the lower end, then
View SolutionThe Young's modulus of steel is twice that of brass. Two wires of the same length and of the same area of cross section, one of steel and another of brass are suspended from the same roof. If we want the lower ends of the wires to be at the same level, then the weight added to the steel and brass wires must be in the ratio of
View SolutionA heavy rope is suspended from the ceiling of a room. If ϕ is the density of the rope, L be its original length and Y be its. Young's modulus, then increase ΔL in the length of the rope due to its own weight is
View SolutionThe sphere at P is given a downward velocity v0 and swings in a vertical plane at the end of a rope of l=1m attached to a support at O. The rope breaks at angle 30∘ from horizontal , knowing that it can withstand a maximum tension equal to three times the weight of the sphere. Then the value of v0 will be :
(g=π2m/s2)
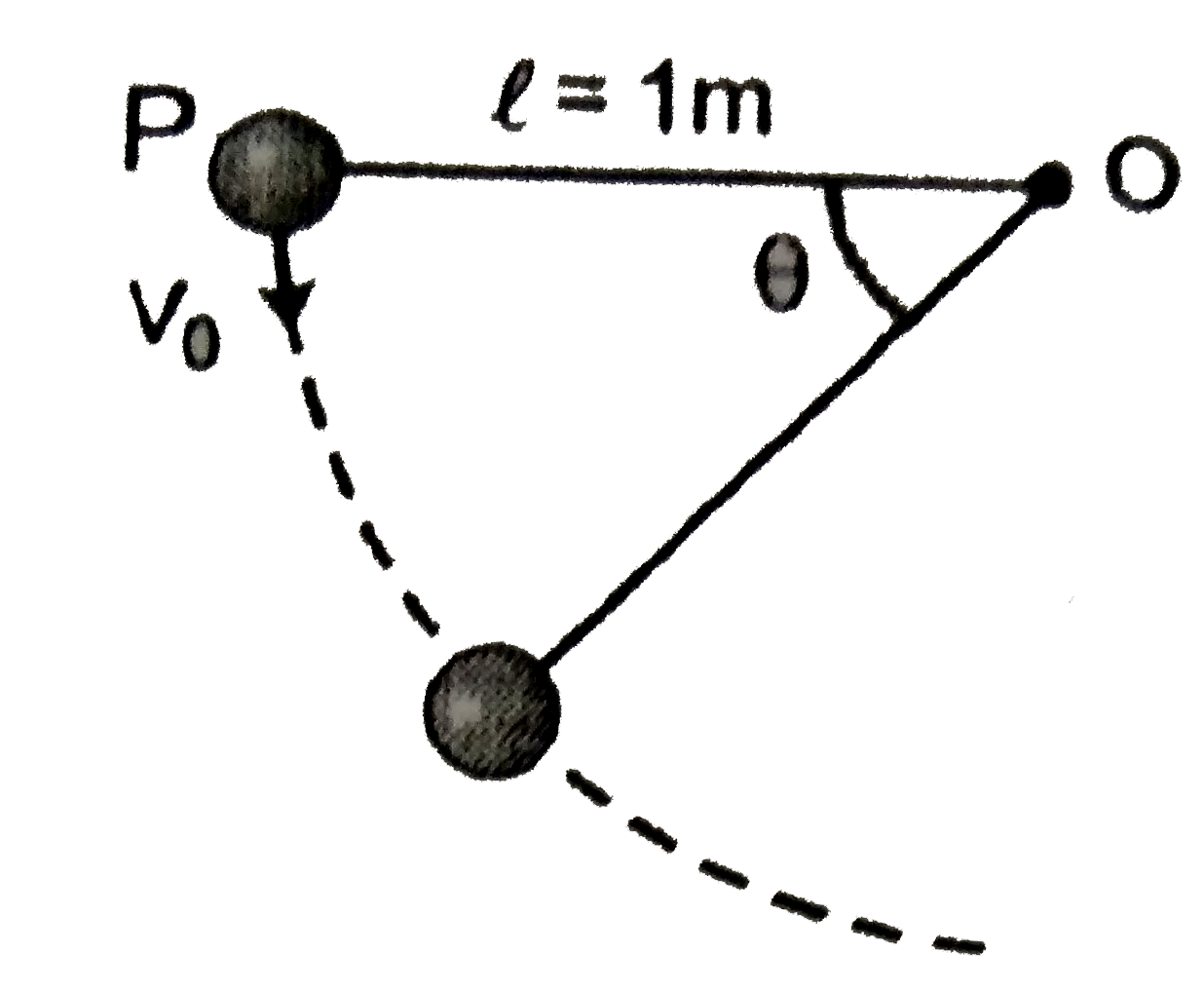
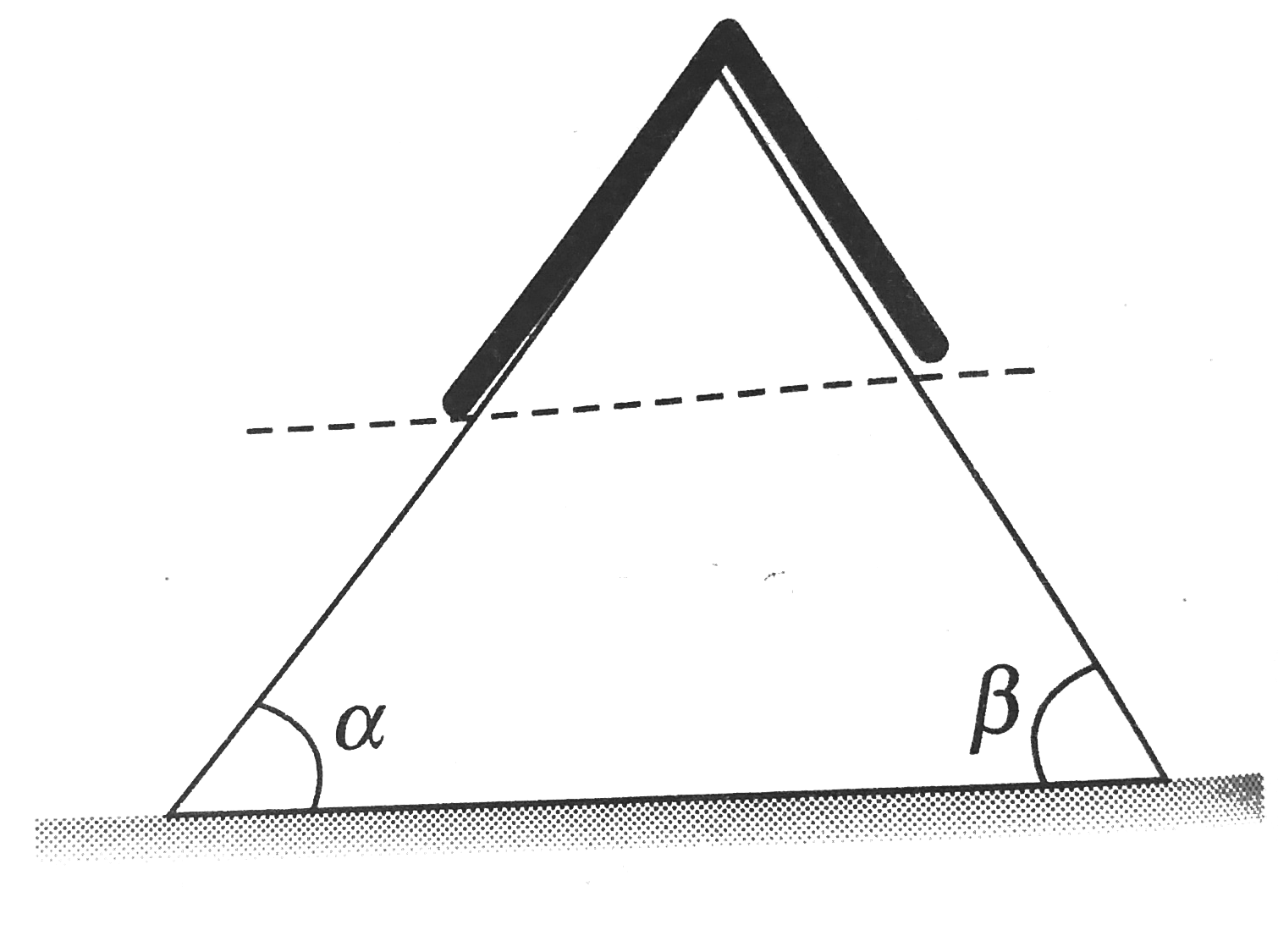
View SolutionA uniform of rope length L and mass M is placed on a smooth fixed wedge as shown. Both ends of rope are at same horizontal level. The rope is initially released from rest, then the magnitude of initial acceleration of rope is.
View Solution
