A heavy box is slid across a rough floor with an initial speed of 4 m/s. It stops moving after 8 seconds. If the average resisting force of friction is 10 N, the mass of the box (in kg) is
40
20
5
2.5
To find the mass of the box, we can follow these steps:
Step 1: Identify the known values
- Initial speed (u) = 4 m/s
- Final speed (v) = 0 m/s (since the box stops)
- Time (t) = 8 seconds
- Average resisting force of friction (F_friction) = 10 N
Step 2: Calculate the acceleration (a)
Using the formula for acceleration:
a=v−ut
Substituting the known values:
a=0−48=−48=−0.5m/s2
Step 3: Relate the friction force to mass and acceleration
According to Newton's second law:
F=m⋅a
Where:
- F is the force (in this case, the friction force)
- m is the mass of the box
- a is the acceleration
We can rearrange this to find the mass:
m=Fa
Step 4: Substitute the known values into the equation
Substituting the values of force and acceleration:
m=10N−0.5m/s2
Step 5: Calculate the mass
m=100.5=20kg
Conclusion
The mass of the box is 20 kg.
---
- Initial speed (u) = 4 m/s
- Final speed (v) = 0 m/s (since the box stops)
- Time (t) = 8 seconds
- Average resisting force of friction (F_friction) = 10 N
Using the formula for acceleration:
a=v−ut
a=0−48=−48=−0.5m/s2
According to Newton's second law:
F=m⋅a
Where:
- F is the force (in this case, the friction force)
- m is the mass of the box
- a is the acceleration
m=Fa
Substituting the values of force and acceleration:
m=10N−0.5m/s2
m=100.5=20kg
The mass of the box is 20 kg.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-B)
44 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-C)
63 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE
69 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
Similar Questions
A 5kg box is moving straight across the floor at a constant speed by a force of 30N as shown in figure

a. How large a friction force impends the motion of the box ?
b. Find μk between the box and the floor
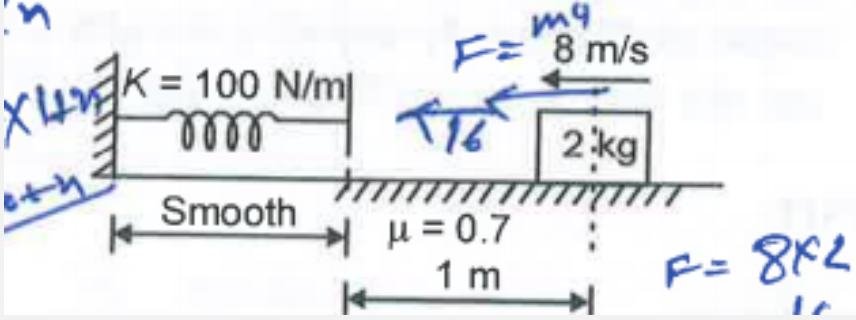
View SolutionFree end of an ideal spring of spring constant 100 N/m is at a distance 1 m from a vertical block of mass 2 kg moving on rough surface with initial speed 8 m/s as shown in figure. If coefficient of friction is 0.7, then maximum compression in spring is (g=10ms−2)
View Solution
Knowledge Check
A bullet of mass 40g moving with a speed of 90ms−1 enters a heavy wooden block and is stopped after a direction of 60cm. The average resistive force exered by the block on the bullet is
A180 NB220 NC270 ND320 NA box with a mass of 2kg accelerates in a straight line from 4 m/s to 8m/s due to the application of a force whose duration is 0.5 s. find the average strength of this force.
A2NB4NC8ND16N
A body of mass 10 kg moves on rough horizontal surface with initial velocity 10m/s and travels 500m before coming to rest. The coefficient of friction is
View SolutionA bullet of mass 0.04 kg moving with a speed of 600 m/s penetrates a heavy wooden block. It stops after a penetration of 500 cm. The resistive force exerted by the block on the bullet is
View SolutionA bullet of mass 40 g moving with a speed of 90ms−1 enters a heavy wooden block and is stopped after a distance of 60 cm . The average resistive force exerted by the block on the bullet is :
View SolutionA particle of mass m is moving with speed u. It is stopped by a force F in distance x if the stopping force is 4 F then
View SolutionA man of mass 80kg pushes box of mass 20kg horizontaly. The man moves the box with a constant acceleration of 2m/s2 but his foot does not slip on the ground. There is no friction between the box and the ground. There is no friction between the box and the ground. whereas there is sufficient friction between the man's foot and the ground to prevent him from slipping.
Assertion:- The force applied by the man on the box is equal and opposite to the force applied by the force applid by the box on the man.
Reason:- Friction force applied by the ground on the man is 200N.
View SolutionA bullet of mass 0.06 kg moving with a speed of 90ms−1 enters a heavy wooden block and it stopped after a distance of 60 cm. What is the average resistive force exerted by the block on the bullet ?
View Solution
