In case of bending of a beam, depression depends on Young modulus of elasticity Y as
∝Y
∝Y2
∝Y−1
∝Y−2
Step by step video & image solution for In case of bending of a beam, depression depends on Young modulus of elasticity Y as by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment(Section-A)
54 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment(Section-B)
26 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment (SECTION - J)
2 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - J
9 Videos
- Mock test 03BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - Mock test 03EXERCISE - EXAMPLE
44 Videos
Similar Questions
Knowledge Check
The temperature of a wire is doubled. The Young's modulus of elasticity
Aalso doubleBbecome four timesCremain sameDdecrease.
Young's modulus of elasticity is the ratio of
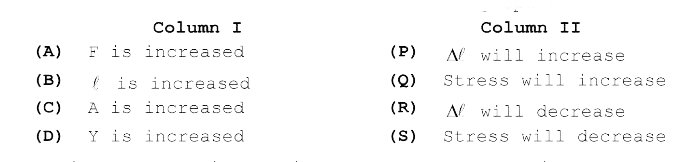
View SolutionA wire of length l, area of cross section A and Young’s modulus of elasticity Y is stretched by a longitudinal force F. The change in length is Δl Match the following two columns.
View SolutionThe temperature of a wire is doubled. The Young's modulus of elasticity
View SolutionAssertion: From the relation Y =FlAΔl, we can say that, if length of a wire is doubled, its young's modulus of elasticity will also becomes two times.
Reason : Modulus of elasticity is a material property.
View SolutionHow many number of wires are used in Searl's experiment for determining Young's modulus of elasticity ?
View SolutionFind the dimensions of stress, strain and modulus of elasticity.
View SolutionA metallic wire is stretched by suspending a weight of it. If α is the longitudinal strain and Y is its Young's modulus of elasticity, then slow that the elastic potential energy per unit volume is given by 12Yα2.
View Solution
