If acceleration due to gravity at distance d [<R] from the centre of earth is β , then its value at distance d above the surface of earth will be [ where R is radius of earth ]
βR2(R+d)3
βR2d
βd(R+d)3
βR3d(R+d)2
The correct Answer is:D
To solve the problem, we need to find the acceleration due to gravity at a distance d above the surface of the Earth, given that the acceleration due to gravity at a distance d inside the Earth (where d<R, with R being the radius of the Earth) is β.
1. Understanding the Acceleration Inside the Earth:
The acceleration due to gravity g at a distance d from the center of the Earth (where d<R) is given by the formula:
g=GMdR3
where G is the universal gravitational constant and M is the mass of the Earth. According to the problem, at this distance d, the acceleration due to gravity is β:
β=GMdR3
2. Finding the Acceleration Above the Surface of the Earth:
Now, we need to find the acceleration due to gravity at a distance d above the surface of the Earth. The distance from the center of the Earth to this point is R+d. The formula for the acceleration due to gravity at this distance is:
g′=GM(R+d)2
3. Expressing GM in Terms of β:
From the first equation, we can express GM in terms of β:
GM=βR3d
4. Substituting GM into the Second Equation:
Now, substitute GM into the equation for g′:
g′=βR3d(R+d)2
5. Final Expression for g′:
Thus, we can simplify this to:
g′=βR3d(R+d)2
Conclusion:
The acceleration due to gravity at a distance d above the surface of the Earth is:
g′=βR3d(R+d)2
The acceleration due to gravity g at a distance d from the center of the Earth (where d<R) is given by the formula:
g=GMdR3
where G is the universal gravitational constant and M is the mass of the Earth. According to the problem, at this distance d, the acceleration due to gravity is β:
β=GMdR3
Now, we need to find the acceleration due to gravity at a distance d above the surface of the Earth. The distance from the center of the Earth to this point is R+d. The formula for the acceleration due to gravity at this distance is:
g′=GM(R+d)2
From the first equation, we can express GM in terms of β:
GM=βR3d
Now, substitute GM into the equation for g′:
g′=βR3d(R+d)2
Thus, we can simplify this to:
g′=βR3d(R+d)2
The acceleration due to gravity at a distance d above the surface of the Earth is:
g′=βR3d(R+d)2
Topper's Solved these Questions
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - C (PREVIOUS YEARS QUESTIONS)
51 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - A (OBJECTIVE TYPE QUESTIONS)
41 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
9 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
Similar Questions
If earth has uniform density, and radius 'R'. The value of acceleration due to gravity at distance d above the surface is same as the acceleration due to gravity at distance d below the surface. If d=(√x−12)R, then find x.
View SolutionWhat will be the acceleration due to gravity at a distance of 3200 km below the surface of the earth ? (Take Re=6400 km)
View Solution
Knowledge Check
The acceleration due to gravity on the moon is
A(16)th that of the earthBsame that of the earthC(13)rd that of the earthD(15)th that of the earth
A satellite of mass m is moving in a circular or orbit of radius R around the earth. The radius of the earth is r and the acceleration due to gravity at the surface of the earth is g. Obtain expressions for the following :
(a) The acceleration due to gravity at a distance R from the centre of the earth
(b) The linear speed of the satellite
(c ) The time period of the satellite
View SolutionIf earth is assumed to be a sphere of uniform density then plot a graph between acceleration due to gravity (g) and distance from the centre of earth.
View SolutionWhich graph correctley presents the variation of acceleration due to gravity with the distance form the centre of the earth?
View SolutionFigure shows variation of acceleration due to gravity with distance from centre of a uniform spherical planet, Radius of planet is R. What is r1−r1
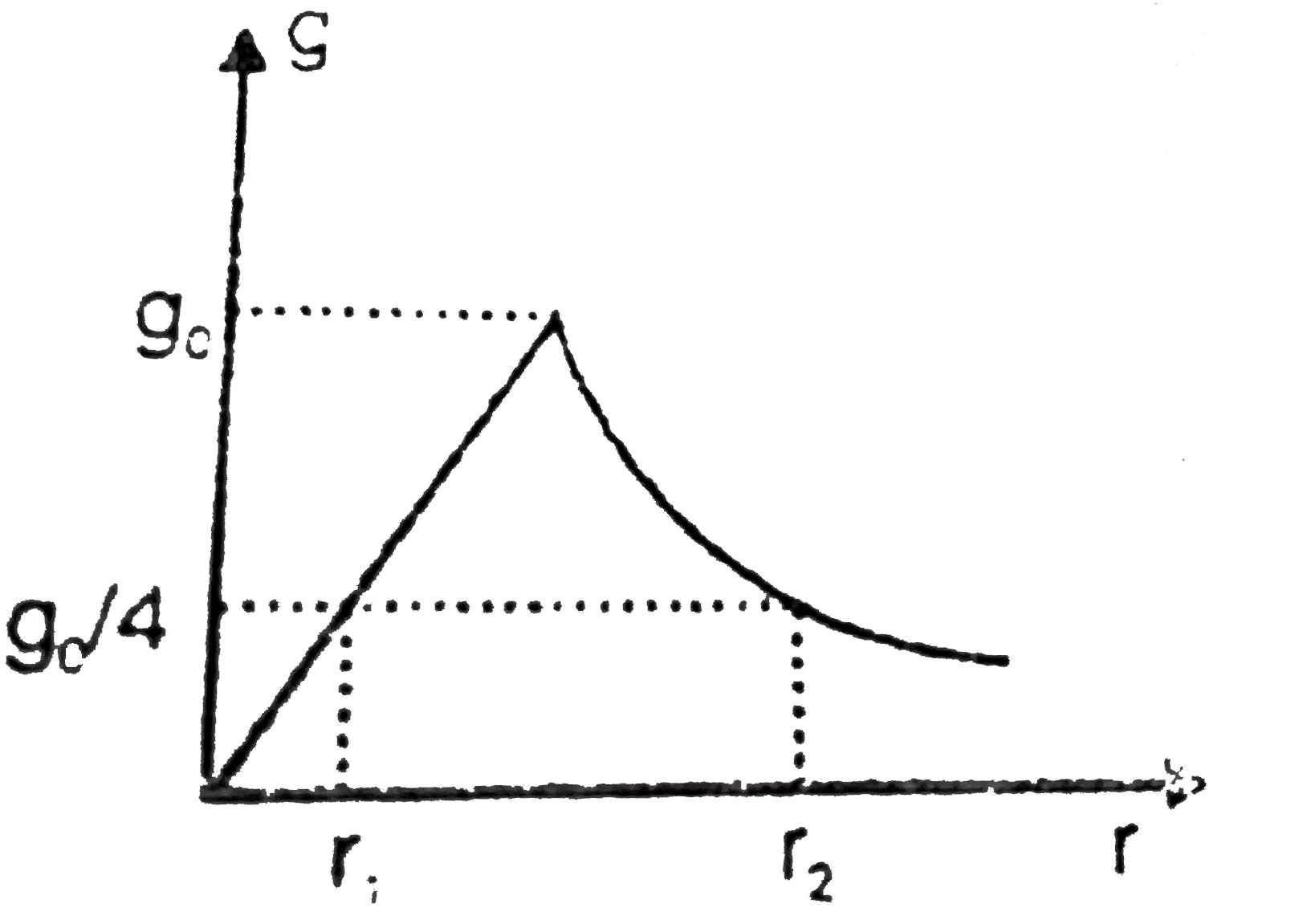
View SolutionAcceleration due to gravity is maximum at
View SolutionThe height above the surface of earth at which acceleration due to gravity is half the acceleration due to gravity at surface of eart is (R=6.4×106m)
View SolutionAcceleration due to gravity at earth's surface is 10m−2 The value of acceleration due to gravity at the surface of a planet of mass 12 th and radius 12 of f the earth is -
View Solution
