The switch shown in the circuit is closed al t = 0, The current drawn from the battery by the circuit at t = 0 and 1=∞ are in the ratio
2:1
1:2
1:1
1:4
The correct Answer is:C
To solve the problem, we need to analyze the behavior of the circuit at two different time instances: when the switch is closed at t=0 and as t approaches infinity.
Step 1: Analyze the circuit at t=0
At t=0:
- The capacitor behaves as a short circuit (since it has not had time to charge).
- The inductor behaves as an open circuit (since it does not allow sudden changes in current).
Given that the capacitor is short-circuited and the inductor is open-circuited, we can redraw the circuit. The only components that will affect the current are the resistors.
Net Resistance at t=0:
- If we have two resistors R and R′ in series, the total resistance Rnet is:
Rnet=R+R′=2R
Current at t=0:
Using Ohm's law, the current I1 drawn from the battery at t=0 is:
I1=ERnet=E2R
Step 2: Analyze the circuit as t→∞
As t approaches infinity:
- The capacitor behaves as an open circuit (fully charged).
- The inductor behaves as a short circuit (it allows steady current to pass through).
In this case, the circuit can again be simplified to just the resistors since the capacitor does not allow current to flow through it.
Net Resistance at t→∞:
- The resistors are still in series, so the total resistance remains:
Rnet=R+R=2R
Current at t→∞:
The current I2 drawn from the battery at t→∞ is:
I2=ERnet=E2R
Step 3: Calculate the ratio of currents
Now, we can find the ratio of the currents I1 and I2:
I1I2=E2RE2R=1
Conclusion
Thus, the ratio of the current drawn from the battery at t=0 and t=∞ is:
Ratio=1:1
Final Answer
The ratio of the current drawn from the battery by the circuit at t=0 and t=∞ is 1:1.
---
At t=0:
- The capacitor behaves as a short circuit (since it has not had time to charge).
- The inductor behaves as an open circuit (since it does not allow sudden changes in current).
- If we have two resistors R and R′ in series, the total resistance Rnet is:
Rnet=R+R′=2R
Using Ohm's law, the current I1 drawn from the battery at t=0 is:
I1=ERnet=E2R
As t approaches infinity:
- The capacitor behaves as an open circuit (fully charged).
- The inductor behaves as a short circuit (it allows steady current to pass through).
- The resistors are still in series, so the total resistance remains:
Rnet=R+R=2R
The current I2 drawn from the battery at t→∞ is:
I2=ERnet=E2R
Now, we can find the ratio of the currents I1 and I2:
I1I2=E2RE2R=1
Thus, the ratio of the current drawn from the battery at t=0 and t=∞ is:
Ratio=1:1
The ratio of the current drawn from the battery by the circuit at t=0 and t=∞ is 1:1.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:AAKASH INSTITUTE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:ASSIGNMENT(SECTION -C) Previous Years Questions
Explore 34 Videos
- ELECTROMAGNETIC INDUCTIONBook:AAKASH INSTITUTE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:ASSIGNMENT(SECTION -D) Assertion-Reason type Question)
Explore 15 Videos
- ELECTROMAGNETIC INDUCTIONBook:AAKASH INSTITUTE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:ASSIGNMENT(SECTION - A) (OBJECTIVE TYPE QUESTIONS)
Explore 35 Videos
- ELECTRIC CHARGES AND FIELDS Book:AAKASH INSTITUTE ENGLISHChapter:ELECTRIC CHARGES AND FIELDS Exercise:comprehension
Explore 3 Videos
- ELECTROMAGNETIC WAVESBook:AAKASH INSTITUTE ENGLISHChapter:ELECTROMAGNETIC WAVESExercise:ASSIGNMENT SECTION - D Assertion-Reason Type Questions
Explore 25 Videos
Similar Questions
Determine the current drawn from the battery in the circuit shown.
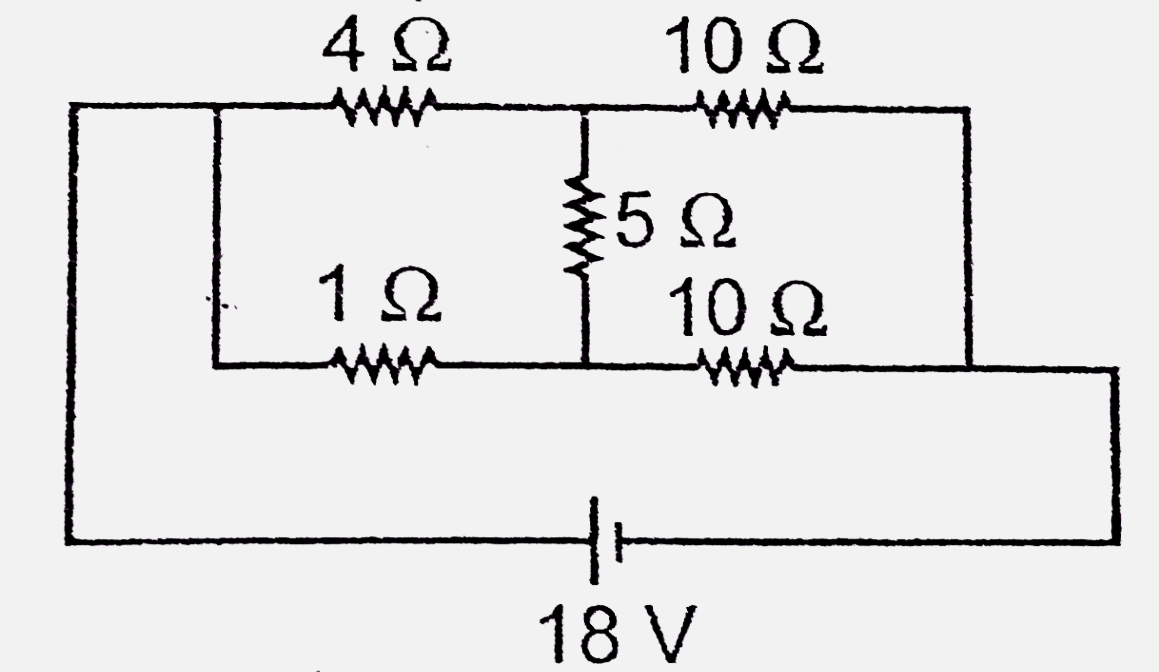
View SolutionIn the circuit shown in the figure, in steady state:
The current drawn from the battery is
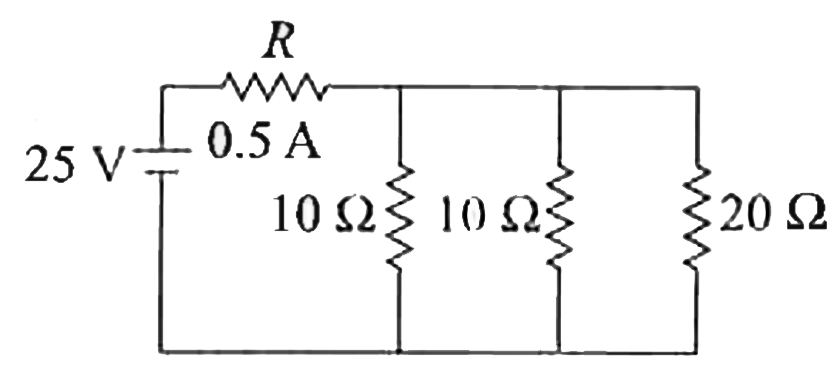
View SolutionIn the circuit as shown if the current drawn through battery is 0.5A. Then
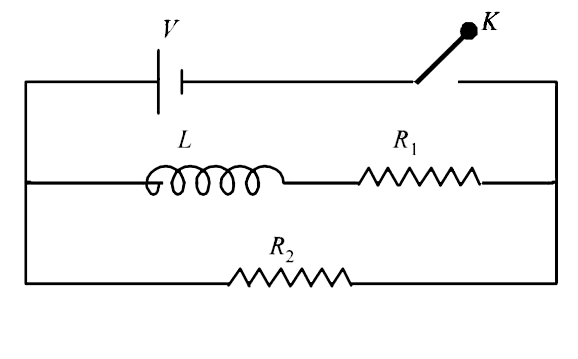
View SolutionIn the circuit shown below, the key K is closed at t = 0. The current through the battery is

View SolutionIn the circuit shown below, the key K is closed at t =0. The current through the battery is
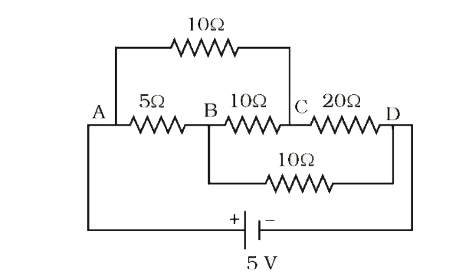
View SolutionCalculate the value of the current drawn from a 5V battery in the circuit as shown
View SolutionThe switch shown in figure is closed at t=0 find the charge throuh battery till time t=LR
_2019_CBT8_E01_016_Q01.png)
View SolutionThe switch shown in figure is closed at t=0 find the charge throuh battery till time t=LR
_2019_CBT8_E01_016_Q01.png)
View SolutionIn the circuit shown in figure switch S is closed at time t=0

Current I from the battery at time t is given by
View SolutionIn the given circuit, what is the current I (in A) drawn from battery at time t = 0.
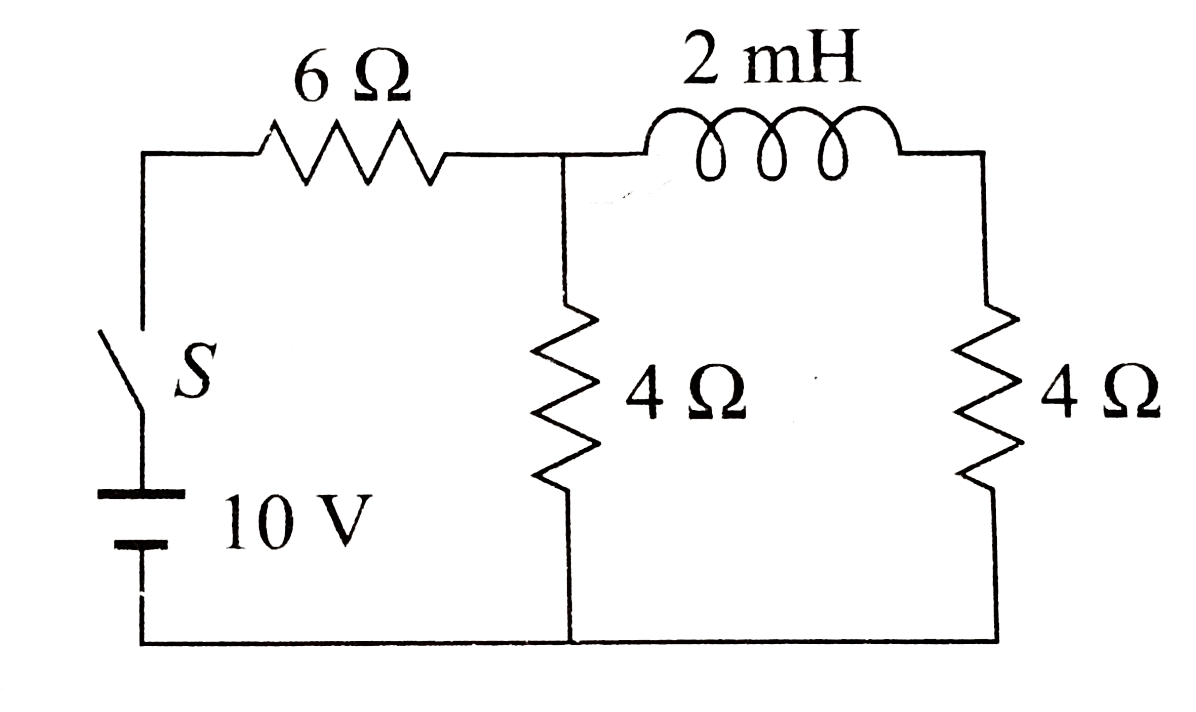
View Solution