The figure shows three circuits with identica batteries, inductors and resistances. Rank the circuits according to the currents through the battery just after the switch is closed, greatest fire
l2>l3>l1
l2>l1>l3
l1>l2>l3
l1>l3>l2
The correct Answer is:A
To solve the problem of ranking the currents through the battery just after the switch is closed in the three circuits, we can follow these steps:
Step 1: Understand the Circuit Configuration
Each circuit consists of identical batteries, inductors, and resistors. The key point to note is that inductors resist changes in current. Just after the switch is closed, the inductors will initially oppose the flow of current.
Step 2: Analyze Each Circuit
- Circuit A: The inductor is in series with the resistors. Initially, the inductor will oppose the current, causing the current (I1) to be very small.
- Circuit B: The inductor is also in series with the resistors, but the configuration may allow for a higher initial current compared to Circuit A. Here, the current (I2) will be higher than I1 because the resistors are arranged to allow more current to flow.
- Circuit C: If the inductor is bypassed or if the configuration allows for a direct path through the resistors, the current (I3) will be the highest among the three circuits, as the inductor's opposition is minimized.
Step 3: Apply Ohm's Law
Using Ohm's Law (V = IR), we can express the currents:
- For Circuit A: I1≈0 (due to the inductor opposing the current)
- For Circuit B: I2=VR (current flows through the resistors)
- For Circuit C: I3=V2R (if the inductor is bypassed, the current is higher)
Step 4: Rank the Currents
From our analysis:
- I2>I3>I1
Thus, the ranking of the currents through the battery just after the switch is closed is:
1. Circuit B (I2)
2. Circuit C (I3)
3. Circuit A (I1)
Final Answer
The ranking of the currents through the battery just after the switch is closed is:
I2 > I3 > I1
Each circuit consists of identical batteries, inductors, and resistors. The key point to note is that inductors resist changes in current. Just after the switch is closed, the inductors will initially oppose the flow of current.
- Circuit A: The inductor is in series with the resistors. Initially, the inductor will oppose the current, causing the current (I1) to be very small.
- Circuit B: The inductor is also in series with the resistors, but the configuration may allow for a higher initial current compared to Circuit A. Here, the current (I2) will be higher than I1 because the resistors are arranged to allow more current to flow.
Using Ohm's Law (V = IR), we can express the currents:
- For Circuit A: I1≈0 (due to the inductor opposing the current)
- For Circuit B: I2=VR (current flows through the resistors)
- For Circuit C: I3=V2R (if the inductor is bypassed, the current is higher)
From our analysis:
- I2>I3>I1
1. Circuit B (I2)
2. Circuit C (I3)
3. Circuit A (I1)
The ranking of the currents through the battery just after the switch is closed is:
I2 > I3 > I1
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT(SECTION -C) Previous Years Questions
34 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT(SECTION -D) Assertion-Reason type Question)
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT(SECTION - A) (OBJECTIVE TYPE QUESTIONS)
35 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - comprehension
3 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
Similar Questions
The figure shows theree cirrcuit with idential batteries, inductors, and resistors. Rank the circuit according to the current through the battery (i) just after the switch is closed and (ii) a long time later, greatest first
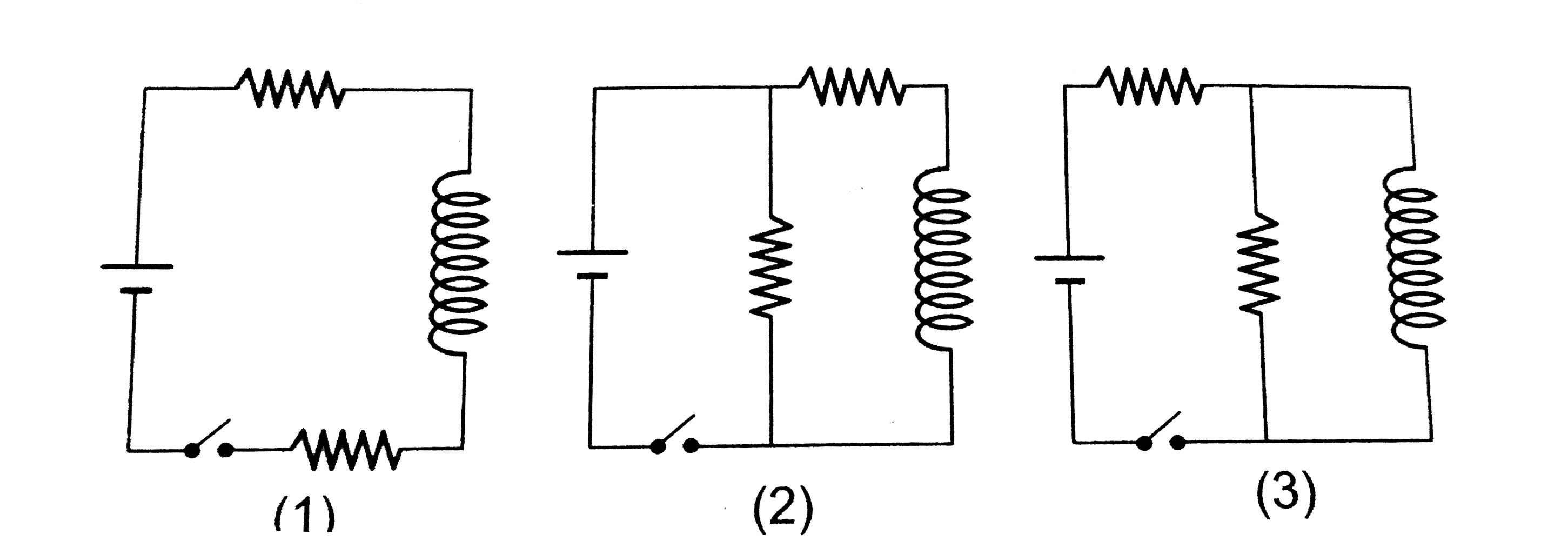
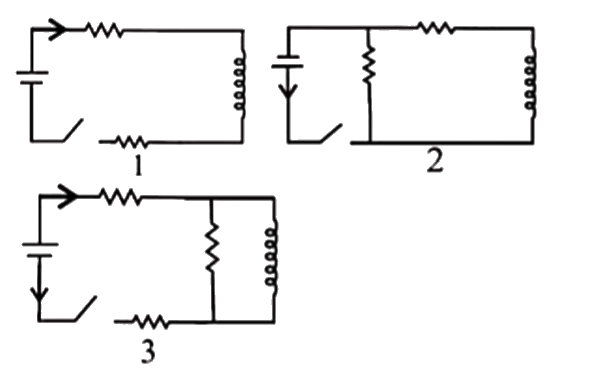
View SolutionThe figure shows three circuits with identical batteries, inductors and resistance . Rank the circuits in decreasing order, according to the current through the battery just after the switch is closed
View SolutionIn the circuit diagram the current through the battery immediately after the switch S is closed is
View SolutionThe current through the battery shown in the circuit is
View SolutionIn the circuit shown, calculate the current through 6V battery

View SolutionIn the following circuit the value of current i through the battery just after switch S is closed is
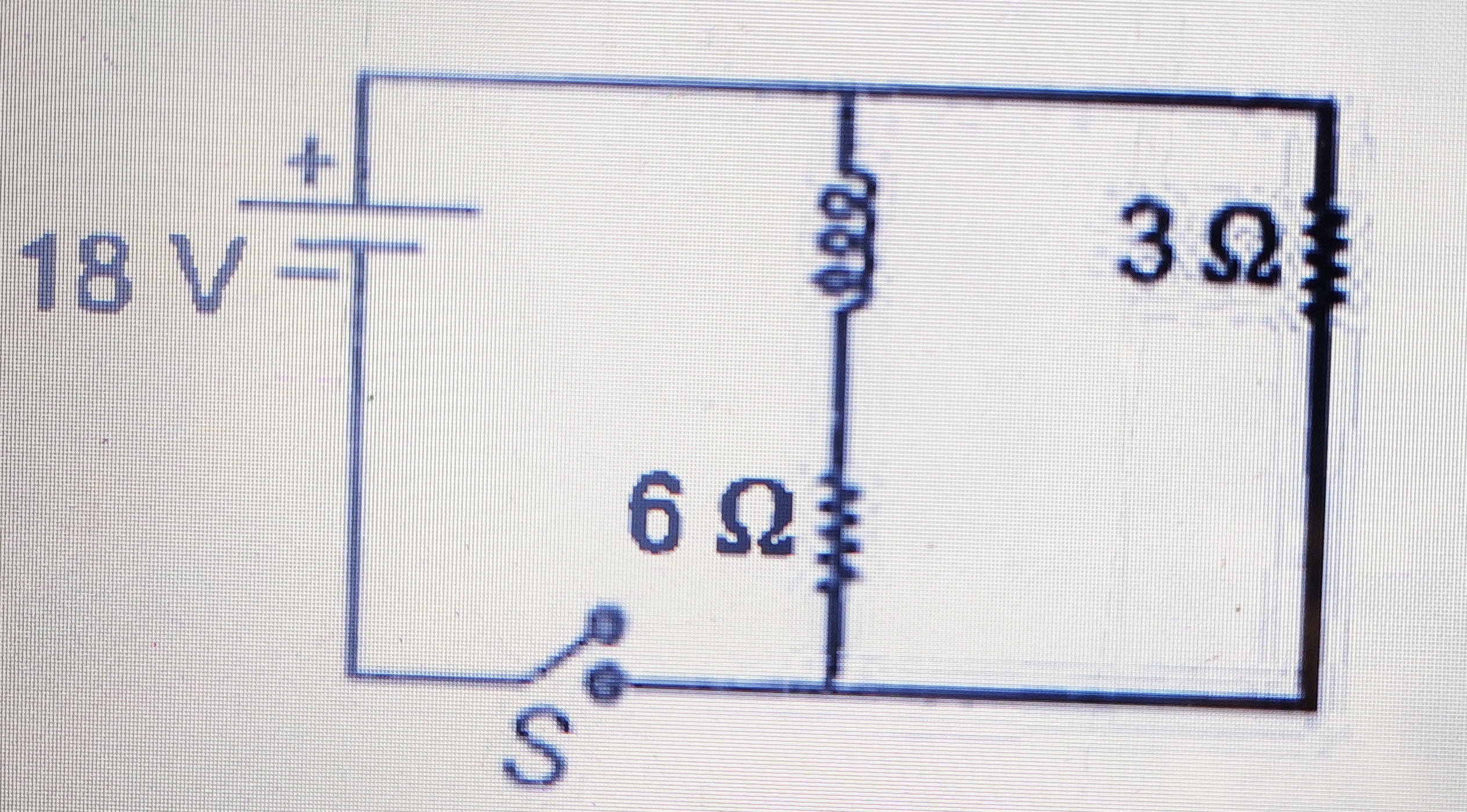
View SolutionCurrent through the battery at the instance when the switch S is closed is
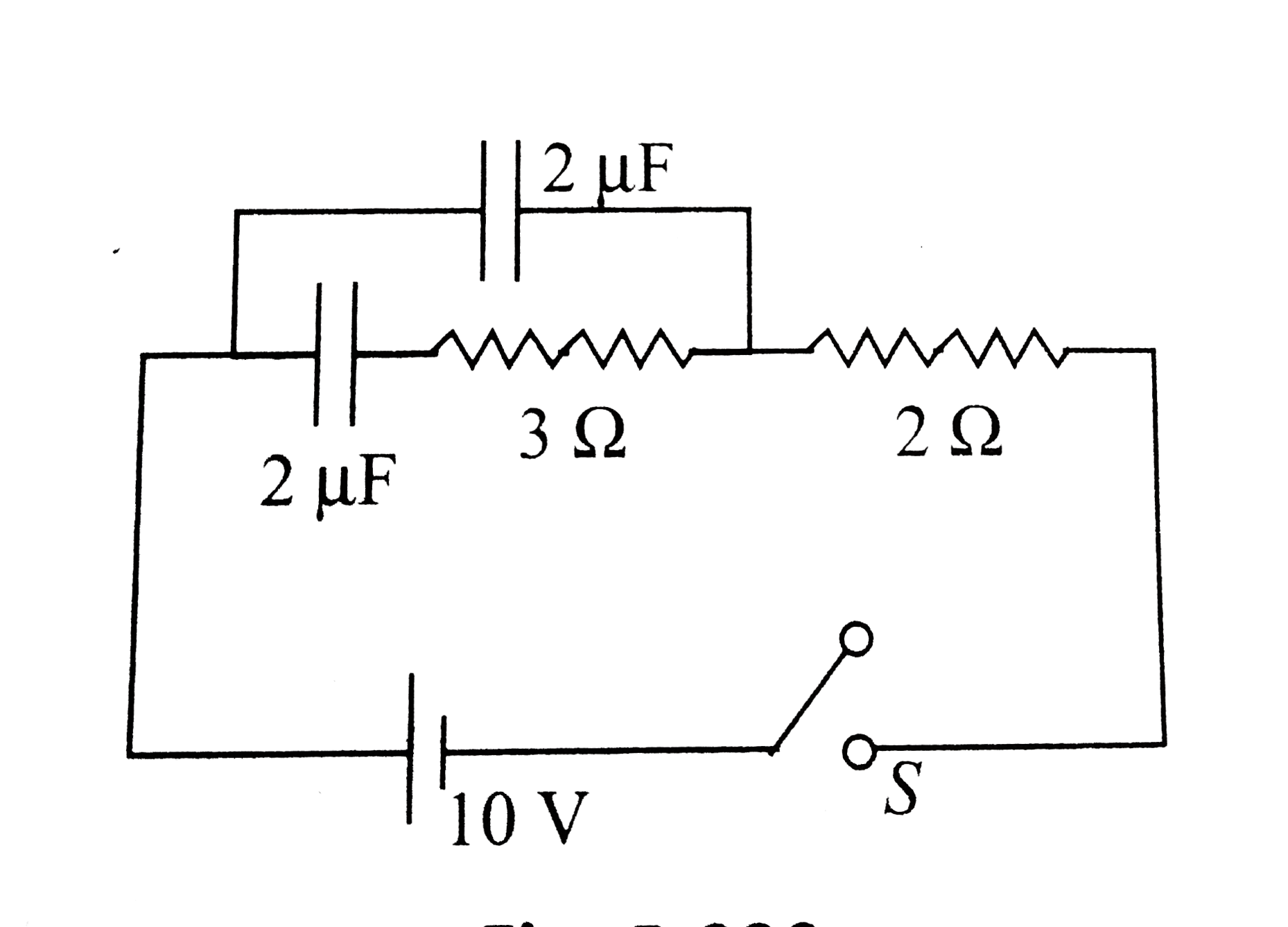
View SolutionConsider the circuit shown in figure. The current through the battery a long time after the switch S is closed is:

View SolutionIn the given circuit,
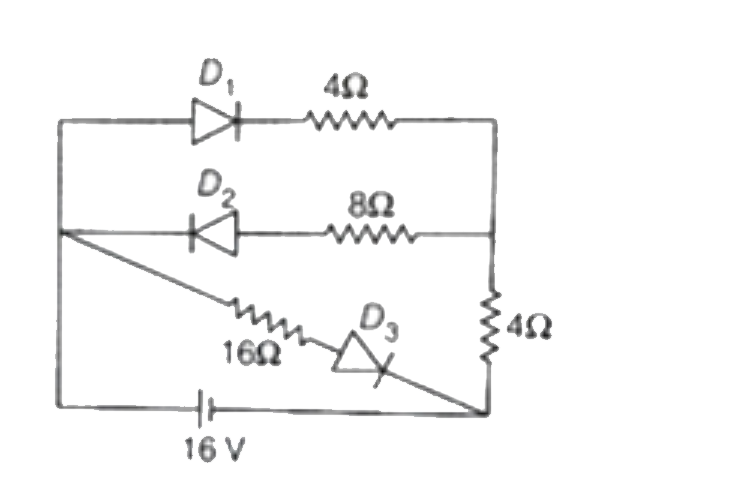
the current through the battery is
View SolutionThe ratio of initial to final current through the battery when the switch is closed in the figure is
View Solution
