If in a planoconvex lens, the radius of curvature of the convex surface is 10cm and the focal length is 30cm, the refractive index of the material of the lens will be
1.5
1.66
1.33
3
The correct Answer is:C
To find the refractive index (μ) of a planoconvex lens given the radius of curvature (R) and the focal length (f), we can use the lens maker's formula:
1f=(μ−1)1R1−(μ−1)1R2
For a planoconvex lens:
- The radius of curvature of the convex surface (R1) is positive: R1=+10cm
- The radius of curvature of the flat surface (R2) is considered infinite: R2=−∞
- The focal length (f) is given as +30cm
Step 1: Substitute the values into the lens maker's formula
Using the values provided:
130=(μ−1)(110−0)
Since 1R2=0 (because R2=−∞), the equation simplifies to:
130=(μ−1)110
Step 2: Rearrange the equation to solve for (μ - 1)
Multiply both sides by 10:
1030=μ−1
13=μ−1
Step 3: Solve for μ
Add 1 to both sides:
μ=1+13
μ=33+13=43
Conclusion
Thus, the refractive index (μ) of the material of the lens is:
μ=43
- The radius of curvature of the convex surface (R1) is positive: R1=+10cm
- The radius of curvature of the flat surface (R2) is considered infinite: R2=−∞
- The focal length (f) is given as +30cm
130=(μ−1)(110−0)
130=(μ−1)110
1030=μ−1
13=μ−1
μ=1+13
μ=33+13=43
μ=43
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - ASSIGNMENT (SECTION - B)
35 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - ASSIGNMENT (SECTION - C)
80 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - EXERCISE
45 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
4 Videos
- SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )EXERCISE - Assignment SECTION - D (Assertion & reason type Question)
10 Videos
Similar Questions
For a plano convex lens, the radius of curvature of convex surface is 10 cm and the focal length is 30 cm. The refractive index of the material of the lens is
View SolutionIf in a plano-convex lens, the radius of curvature of the convex surface is 10 cm and the focal length of the lens is 30 cm , then the refractive index of the material of lens will be
View Solution
Knowledge Check
The radius of curvature of the curved surface of a plano-convex lens is 20cm. If the refractive index of the material of the lens be 1.5, it will
Aact as a convex lens only for the objects that lie on its curved side.Bact as a concave lens for the objects that lie on its curved side.Cact as a convex lens irrespective of the side on which the object lies.Dact as a concave lens irrespective of side on which the object lies.The power of a biconvex lens is 10 dioptre and the radius of curvature of each surface is 10 cm. Then the refractive index of the material of the lens is
A32B43C98D53
Find the radius of curvature of the convex surface of a plan-convex lens, whose focal length is 0.3 m and the refractive index of the material of the lens is 1.5.
View SolutionThe radius of curvature of the convex surface of a thin plano-convex lens is 12 cm, and the refractive index of its material is 1.6. What is the power of lens ?
View SolutionThe radius of curvature of the convex face of a plano convex lens is 12cm and the refractive index of the material of the lends 1.5. Then, the focal length of the lens is
View SolutionA plano convex lens has radius of curvature 10 cm. Its focal length is 80 cm under water. Calculate the refractive index of the material of the lens, given refractive index of water is 4/3.
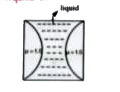
View SolutionThe effective focal length of the lens combination shown in figure is -60 cm. The radius of curvature of the curved surfaces of the plano-convex lenses are 12 cm each and refractive index of the material of the lens is 1.5. The refractive index of the liquid is
View SolutionA double convex lens has focal length 25 cm. The radius of curvature of one of the surfaces is double of the other. Find the radii, if the refractive index of the material of the lens is 1.5.
View Solution
