The focal length of a planoconvex glass lens is 20 cm (μg=1.5). The plane face of it is silvered. An illuminating object is placed at a distance of 60 cm from the lens on its axis along the convex side. Then the distance (in cm) of the image is
20
30
40
12
The correct Answer is:D
To solve the problem step by step, we will follow these steps:
Step 1: Identify the given data
- Focal length of the plano-convex lens, f=20cm
- Refractive index of glass, μg=1.5
- Object distance, u=−60cm (negative because the object is on the same side as the incoming light)
Step 2: Determine the equivalent focal length of the silvered plano-convex lens
Since the plane face of the lens is silvered, it behaves like a concave mirror. The equivalent focal length f′ of the system can be calculated using the formula for the power of the lens and the mirror.
1. The power of the lens PL is given by:
PL=1f=120cm−1
2. The power of the plane mirror PM is zero because the focal length of a plane mirror is infinite:
PM=0
3. The equivalent power P of the system (lens + mirror) is:
P=PL+PM=120+0=120cm−1
4. The equivalent focal length f′ of the silvered lens is:
1f′=P⇒f′=20cm
However, since the plane face is silvered, we need to consider that the effective focal length of a silvered plano-convex lens is given by:
f′=f2=202=10cm
But since it's a concave mirror, we take it as negative:
f′=−10cm
Step 3: Apply the mirror formula
The mirror formula is given by:
1f′=1v+1u
Substituting the values:
1−10=1v+1−60
Step 4: Solve for v
Rearranging the equation:
1v=1−10+160
Finding a common denominator (which is 60):
1v=−6+160=−560
Thus:
1v=−112
So:
v=−12cm
Step 5: Conclusion
The negative sign indicates that the image is formed on the same side as the object, which is consistent with the behavior of a concave mirror. Therefore, the distance of the image from the lens is 12cm.
Final Answer
The distance of the image is 12cm.
---
- Focal length of the plano-convex lens, f=20cm
- Refractive index of glass, μg=1.5
- Object distance, u=−60cm (negative because the object is on the same side as the incoming light)
Since the plane face of the lens is silvered, it behaves like a concave mirror. The equivalent focal length f′ of the system can be calculated using the formula for the power of the lens and the mirror.
PL=1f=120cm−1
PM=0
P=PL+PM=120+0=120cm−1
1f′=P⇒f′=20cm
f′=f2=202=10cm
But since it's a concave mirror, we take it as negative:
f′=−10cm
The mirror formula is given by:
1f′=1v+1u
Substituting the values:
1−10=1v+1−60
Rearranging the equation:
1v=1−10+160
1v=−6+160=−560
Thus:
1v=−112
So:
v=−12cm
The negative sign indicates that the image is formed on the same side as the object, which is consistent with the behavior of a concave mirror. Therefore, the distance of the image from the lens is 12cm.
The distance of the image is 12cm.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - ASSIGNMENT (SECTION - B)
35 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - ASSIGNMENT (SECTION - C)
80 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - EXERCISE
45 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
4 Videos
- SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )EXERCISE - Assignment SECTION - D (Assertion & reason type Question)
10 Videos
Similar Questions
An object is placed at a distance of 12 cm from a convex lens of focal length 8 cm. Find :
nature of the image
View SolutionAn object is placed at a distance of 12 cm from a convex lens of focal length 8 cm. Find :
the position of the image
View SolutionAn object is placed at a distance 24 cm in front of a convex lens of focal length 8 cm.
Calculate the distance of the image from the lens.
View SolutionAn object is placed at a distance 20 cm from the pole of a convex mirror of focal length 20 cm. The image is produced at
View SolutionThe plane surface of a plano-convex lens of focal length 60 cm is silvered. A point object is placed at a distance 20 cm from the lens. Find the position and nature of the final image formed.
View SolutionA convex lens of focal length 10 cm is painted black at the middle portion as shown in figure. An object placed at a distance of 20 cm from the lens. Then
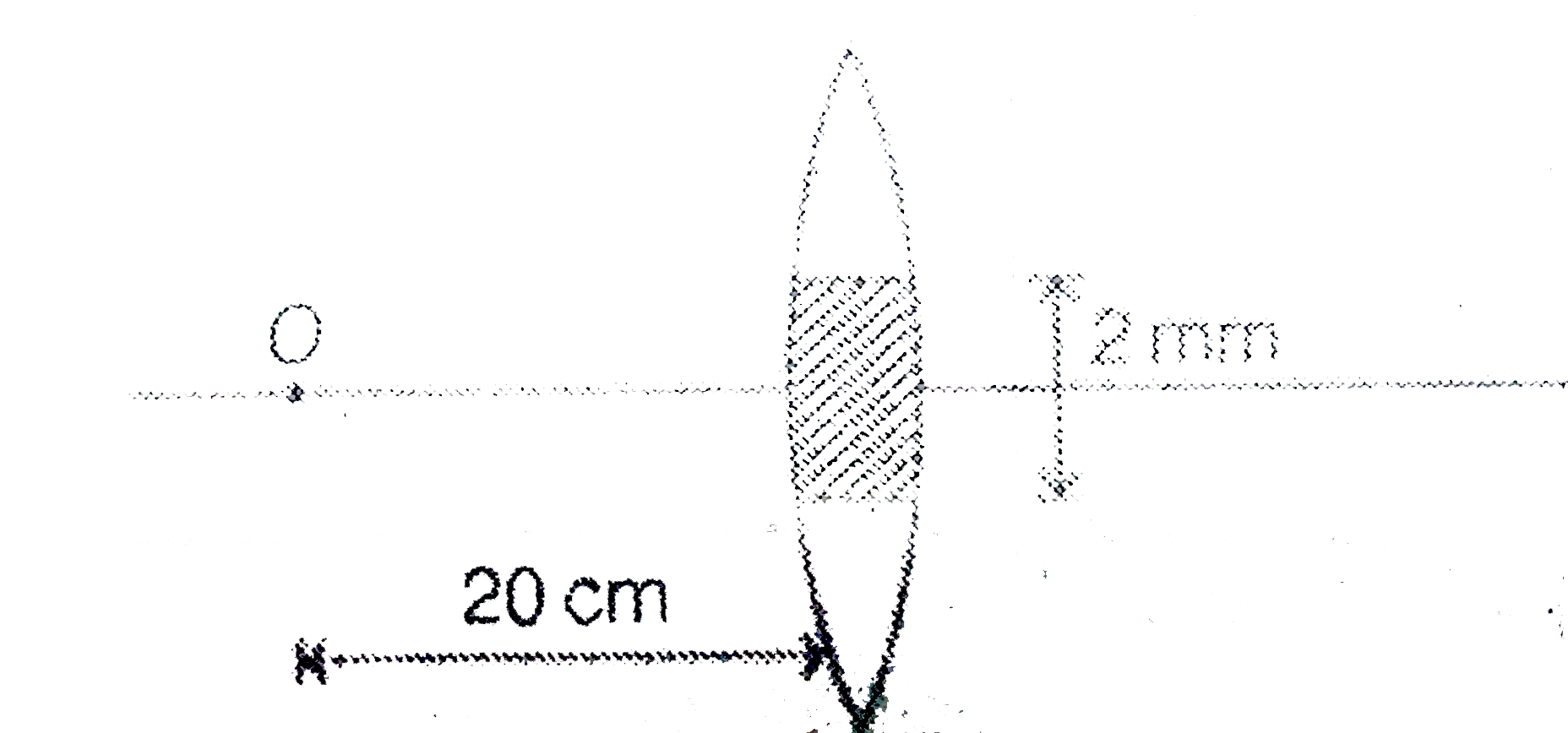
View SolutionFind distanace of image from a convex lens of focal length
20cm if object is placed at a distance of 30cm from the lens. Also find its
magnification.
View SolutionA point object is placed at a distance of 20cm from a thin plano-convex lens of focal length 15cm(μ=1.5). The curved surface is silvered. The image will form at

View SolutionA point object is placed at a distance of 20cm from a thin plano-convex lens of focal length 15cm(μ=1.5). The curved surface is silvered. The image will form at

View SolutionPlane surface of a thin plano-convex lens is silvered. If a point object is placed on principal axis at a distance 60cm from the lens and fial image is formed at a distance 30cm from the lens on same side. What will be the distance of final imagge from the lens if the plane surface is not silvered.
View Solution
