Assertion : If light is polarised by reflection, then the angle between reflected and refracted ray is 180∘.
Reason : Brewester's law : μ=tanip.
π
π/2
2π
π/4
The correct Answer is:B
To solve the given problem, we need to analyze the assertion and the reason provided in the question step by step.
1. Understanding the Assertion:
- The assertion states that if light is polarized by reflection, then the angle between the reflected ray and the refracted ray is 180∘.
- This means that the reflected ray and the refracted ray are in opposite directions.
2. Analyzing the Situation:
- When light hits a surface and is polarized by reflection, it follows Brewster's law. At the polarizing angle ip, the reflected light is completely polarized.
- The angle of incidence ip is equal to the angle of reflection r. The angle of refraction r′ can be determined using Snell's law.
3. Applying Brewster's Law:
- According to Brewster's law, the relationship between the refractive index μ of the medium and the polarizing angle ip is given by:
μ=tan(ip)
- This means that at the polarizing angle, the reflected and refracted rays are not in opposite directions but rather at a specific angle to each other.
4. Calculating the Angles:
- When the light is polarized, the angle between the reflected ray and the refracted ray is actually 90∘ (not 180∘).
- Therefore, the assertion that the angle between the reflected and refracted ray is 180∘ is incorrect.
5. Evaluating the Reason:
- The reason states Brewster's law, which is indeed correct. It provides the correct relationship between the refractive index and the polarizing angle.
6. Conclusion:
- Since the assertion is false and the reason is true, we conclude that the correct answer is that the assertion is false and the reason is true.
Final Answer:
- Assertion: False
- Reason: True
- The assertion states that if light is polarized by reflection, then the angle between the reflected ray and the refracted ray is 180∘.
- This means that the reflected ray and the refracted ray are in opposite directions.
- When light hits a surface and is polarized by reflection, it follows Brewster's law. At the polarizing angle ip, the reflected light is completely polarized.
- The angle of incidence ip is equal to the angle of reflection r. The angle of refraction r′ can be determined using Snell's law.
- According to Brewster's law, the relationship between the refractive index μ of the medium and the polarizing angle ip is given by:
μ=tan(ip)
- This means that at the polarizing angle, the reflected and refracted rays are not in opposite directions but rather at a specific angle to each other.
- When the light is polarized, the angle between the reflected ray and the refracted ray is actually 90∘ (not 180∘).
- Therefore, the assertion that the angle between the reflected and refracted ray is 180∘ is incorrect.
- The reason states Brewster's law, which is indeed correct. It provides the correct relationship between the refractive index and the polarizing angle.
- Since the assertion is false and the reason is true, we conclude that the correct answer is that the assertion is false and the reason is true.
- Assertion: False
- Reason: True
Similar Questions
A ray of light-is incident on glass at the polarising angle ip. Find the angle between the reflected and refracted rays.
View SolutionA beam of light is partially reflected and partially refracted from a surface. The angle between reflected and refracted light ray is 90∘. If the angle of refraction is 30∘, the angle of incidence is
View SolutionAngle of reflection is the angle between the reflected ray and the ………………. incident ray/normal).
View SolutionIf the angle of reflection is 45∘, what is the angle between the incident ray and the reflected ray?
View SolutionLet the refractive index of a denser medium with respect to a rarer medium be n12 and its critical angle be θc. At an angle of incidence A when light is travelling from denser medium to rarer medium, a part of the light is reflected and the rest is refracted and the angle between reflected and refracted rays is 90∘, Angle A given by -
View SolutionLet the refractive index of a denser medium with respect to a rarer medium be n12 and its critical angle be θc. At an angle of incidence A when light is travelling from denser medium to rarer medium, a part of the light is reflected and the rest is refracted and the angle between reflected and refracted rays is 90∘, Angle A given by -
View SolutionIn the figure given the angle between incident ray and the reflected ray is 70∘
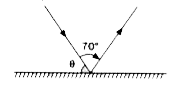
Find the angle of reflection.
View SolutionWhen light is polarised by reflection from a transparent surface.
a) reflection and refracted rays are mutually perpendicular
b) both reflected and refracted rays are plane polarised
c) refraction ray is partially polarised
d) the R.I., of transparent surface is equal to tangent of Brewster.s angle
View SolutionIf the angle of incidence is 32∘, then what will the angle between incident ray and reflected ray?
View SolutionA ray of light is incident on a transparent medium at polarizing angle. What is the angle between the reflected ray and the refracted ray .
View Solution
