Approximate thickness of oil film to observe interference of light (due to which it looks coloured) is
10 mm
10−3mm
10±
1 cm
The correct Answer is:B
To find the approximate thickness of an oil film required to observe interference of light, we need to consider the wavelength of visible light and how it relates to the thickness of the film.
1. Understanding the Concept of Interference:
- Interference of light occurs when light waves overlap and combine, leading to a pattern of bright and dark fringes. For this to happen, the thickness of the film must be comparable to the wavelength of visible light.
2. Identifying the Wavelength Range:
- The wavelength of visible light ranges from approximately 4000 Å (angstroms) to 8000 Å.
- In meters, this range is:
- 4000 Å = 4000 × 10^-10 m = 4 × 10^-7 m
- 8000 Å = 8000 × 10^-10 m = 8 × 10^-7 m
3. Converting Wavelength to Millimeters:
- To convert the wavelengths from meters to millimeters:
- 1 meter = 1000 millimeters
- Therefore,
- 4000 Å = 4 × 10^-7 m = 4 × 10^-4 mm
- 8000 Å = 8 × 10^-7 m = 8 × 10^-4 mm
4. Determining the Approximate Thickness:
- The thickness of the oil film should be on the order of the wavelength of visible light, which is approximately between 4 × 10^-4 mm and 8 × 10^-4 mm.
- Thus, the approximate thickness of the oil film is around 8 × 10^-4 mm.
5. Choosing the Closest Option:
- Now, we compare our calculated thickness with the given options:
- Option 1: 10 mm
- Option 2: 10^-3 mm (which is 0.001 mm)
- Option 3: ±10 (not a valid thickness)
- Option 4: 1 cm (which is 10 mm)
- The closest value to 8 × 10^-4 mm is Option 2: 10^-3 mm.
Conclusion:
The approximate thickness of the oil film to observe interference of light is best represented by Option 2: 10^-3 mm.
- Interference of light occurs when light waves overlap and combine, leading to a pattern of bright and dark fringes. For this to happen, the thickness of the film must be comparable to the wavelength of visible light.
- The wavelength of visible light ranges from approximately 4000 Å (angstroms) to 8000 Å.
- In meters, this range is:
- 4000 Å = 4000 × 10^-10 m = 4 × 10^-7 m
- 8000 Å = 8000 × 10^-10 m = 8 × 10^-7 m
- To convert the wavelengths from meters to millimeters:
- 1 meter = 1000 millimeters
- Therefore,
- 4000 Å = 4 × 10^-7 m = 4 × 10^-4 mm
- 8000 Å = 8 × 10^-7 m = 8 × 10^-4 mm
- The thickness of the oil film should be on the order of the wavelength of visible light, which is approximately between 4 × 10^-4 mm and 8 × 10^-4 mm.
- Thus, the approximate thickness of the oil film is around 8 × 10^-4 mm.
- Now, we compare our calculated thickness with the given options:
- Option 1: 10 mm
- Option 2: 10^-3 mm (which is 0.001 mm)
- Option 3: ±10 (not a valid thickness)
- Option 4: 1 cm (which is 10 mm)
- The closest value to 8 × 10^-4 mm is Option 2: 10^-3 mm.
The approximate thickness of the oil film to observe interference of light is best represented by Option 2: 10^-3 mm.
Similar Questions
What is the minimum thickness of thin film required for constructive interference in the reflected light through it ?
(Given, the refractive index of the film =1.5, wavelength of the lilght incident on the film =600 nm.
View SolutionA ray of light is incident at an angle of 45∘ (ralative to the normal) on a thin film of a liquid with an index of refraction of √2. Assuming that the medium of both sides of the film is air, find the minimum thickness of the film required for constructive interference in the reflected light for sodium light of wavelenght 600 nm.
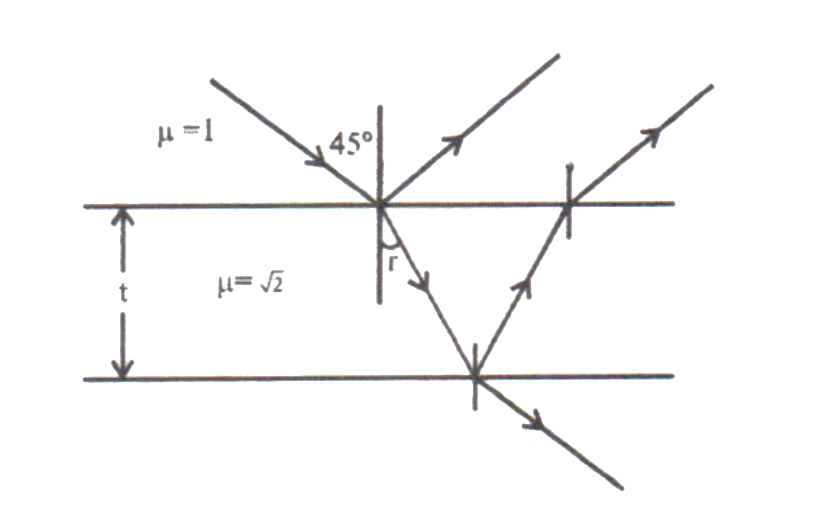
View Solution
Knowledge Check
What is the minimum thickness of a soap bubble needed for constructive interference in reflected light, if the light incident on the film is 750 nm? Assume that the refractive index for the film is n=1.33
A282 nmB70.5 nmC141 nmD387 nmAssertion : The fringe closest on either side of the central white fringe in case of interference pattern due to white light is red and the farthest appears blue.
Reason : The interference patterns due to different component colours of white light overlap.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false.
Refractive index of a thin soap film of a uniform thickness is 1.38. The smallest thickness of the film that gives an interference maxima in the reflected light when light of wavelength 5520 Å falls at normal incidence is
View SolutionRefractive index of a thin soap film of a uniform thickness is 1.34. Find the smallest thickness of the film that gives in interference maximum in the reflected light when light of wavelength 5360Å fall at normal incidence.
View SolutionWhat is the minimum thickness of a soap bubble needed for constructive interference in reflected light, if the light incident on the film is 750 nm? Assume that the refractive index for the film is n=1.33
View SolutionAn oil film covers the surface of a small pond. The refractive index of the oil is greater than that of water. At one point on the film, the film has the smallest non-zero thickness for which there will be destructive interference in the reflected light when infrared radiation with wavelength 800 nm is incident normal to the film. When this film is viewed at normal incidence at this same point, for what visible wavelengths, if any, will there be constructive interference? (Visible light has wavelengths between 400nm and 700 nm )
View SolutionWhat is the minimum thickness of a thin film (μ=1.2) that results in constructive interference in the reflected light? If the film is illuminated with light whose wavelength in free space is λ=500nm ?
View SolutionCalculate the minimum thickness of a soap bubble film (μ=1.33)that results in constructive interference in the reflected light if the film is illuminated with light whose wavelength in free space is λ=600nm.
View Solution
