A current I flows in a thin wire in the shape of a regular polygon n sides. The magnetic induction at the centre of the polygon when n→∞ is (R is the radius of its circumcircle)
μ0ni2πRtanπ6
μ0ni2πRtanπR
μ0i2R
zero
The correct Answer is:C
To find the magnetic induction (magnetic field) at the center of a regular polygon with n sides when n tends to infinity, we can follow these steps:
1. Understanding the Geometry:
- Consider a regular polygon with n sides inscribed in a circle of radius R (the circumradius).
- The angle subtended by each side at the center O of the polygon is 2πn.
2. Identifying the Magnetic Field Contribution:
- The magnetic field B at the center due to one side of the polygon can be calculated using the Biot-Savart law.
- For a finite length of wire, the magnetic field at a distance D from the wire carrying current I is given by:
B=μ0I4πD∫sinθdL
- Here, θ is the angle between the wire and the line connecting the wire to the point where we measure the field.
3. Calculating the Distance:
- The distance D from the center to the midpoint of each side of the polygon is Rcos(πn).
4. Calculating the Total Magnetic Field:
- The total magnetic field at the center due to all n sides can be expressed as:
B=μ0nI4πRcos(πn)(sin(πn)+sin(πn))
- This simplifies to:
B=μ0nI4πRcos(πn)⋅2sin(πn)
5. Simplifying the Expression:
- Further simplifying gives:
B=μ0nI2R⋅sin(πn)cos(πn)
- Using the identity tan(πn) gives:
B=μ0nI2Rtan(πn)
6. Taking the Limit as n→∞:
- As n approaches infinity, tan(πn)≈πn.
- Thus, we have:
B≈μ0I2R
7. Final Result:
- Therefore, the magnetic induction at the center of the polygon when n tends to infinity is:
B=μ0I2R
- Consider a regular polygon with n sides inscribed in a circle of radius R (the circumradius).
- The angle subtended by each side at the center O of the polygon is 2πn.
- The magnetic field B at the center due to one side of the polygon can be calculated using the Biot-Savart law.
- For a finite length of wire, the magnetic field at a distance D from the wire carrying current I is given by:
B=μ0I4πD∫sinθdL
- Here, θ is the angle between the wire and the line connecting the wire to the point where we measure the field.
- The distance D from the center to the midpoint of each side of the polygon is Rcos(πn).
- The total magnetic field at the center due to all n sides can be expressed as:
B=μ0nI4πRcos(πn)(sin(πn)+sin(πn))
- This simplifies to:
B=μ0nI4πRcos(πn)⋅2sin(πn)
- Further simplifying gives:
B=μ0nI2R⋅sin(πn)cos(πn)
- Using the identity tan(πn) gives:
B=μ0nI2Rtan(πn)
- As n approaches infinity, tan(πn)≈πn.
- Thus, we have:
B≈μ0I2R
- Therefore, the magnetic induction at the center of the polygon when n tends to infinity is:
B=μ0I2R
Topper's Solved these Questions
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION C
47 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D
16 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - ASSIGNMENT (SECTION A)
34 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - J)
2 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Assignment Section J (Aakash Challengers Questions)
5 Videos
Similar Questions
Current 'i' is flowing in heaxagonal coil of side a. The magnetic induction at the centre of the coil will be
View SolutionA current I flows along a triangle loop having sides of equal length a. The strength of magnetic field at the centre of the loop is :
View SolutionA current I flows through a thin wire shaped as regular polygon of n sides which can be inscribed in a circle of radius R. The magnetic field induction at the center of polygon due to one side of the polygon is
View SolutionA current I flows through a thin wire shaped as regular polygon of n sides which can be inscribed in a circle of radius R. The magnetic fidl induction at the center of polygon due to one side of the polygon is
View SolutionThe current I ampere is flowing in an equilateral triangle of side a the magnetic field induction at the centroid will be
View SolutionIf a regular polygon of n sides has circum radius R and inradius r then each side of polygon is:
View SolutionThe number of triangles that can be formed form a regular polygon of 2n + 1 sides such that the centre of the polygon lies inside the triangle is
View SolutionIf r is the radius of inscribed circle of a regular polygon of n-sides ,then r is equal to
View SolutionCurrent I A flowing in a circular coil of radius r. then the magnetic induction at the centre is B. If the current is doubled then the magnetic induction will be
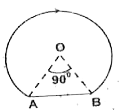
View SolutionA current I flows along a thin wire shaped as shown in figure. The radius of the curved part of the wire is r. The field at the centre O of the coil is:
View Solution
