If the planes of two identical concentric coils are perpendicular and the magnetic moment of each coil is M, then the resultant magnetic moment of the two coils wil be
M
2M
3M
√2M
The correct Answer is:D
Step by step video & image solution for If the planes of two identical concentric coils are perpendicular and the magnetic moment of each coil is M, then the resultant magnetic moment of the two coils wil be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION C47videos
MOVING CHARGE AND MAGNESIUM
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D16videos
MOVING CHARGE AND MAGNESIUM
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - ASSIGNMENT (SECTION A)34videos
MOVING CHARGE AND MAGNESIUM
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - J)2videos
MOTION IN STRAIGHT LINE
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Assignment Section J (Aakash Challengers Questions)5videos
MOVING CHARGES AND MAGNETISM
Similar Questions
A circular coil of Radius R is folded across its diameter such that the planes of two half rings are perpendicular to each other as shown in the figure. If the current through the coil is calculate the magnetic dipole moment of the configuration so formed.
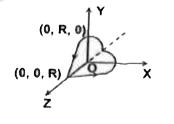 View Solution
View SolutionTwo identical coils have· a common centre and their planes are at right angles to each other and carry equal currents. If the magnitude of the induction field at the centre due to one of the coil is 'B ', then the resultant magnetic induction field due to combination at their common centre is
View Solution
Knowledge Check
- Question 1 - Select One
In the question number 73, for the coil given the magnetic moment is
A12.95Am2B25.79Am2C10.05Am2D24.79Am2
Two magnets of moment M and 2 M are tied at an angle of 60∘ to each other . What is the resultant magnetic moment of the combination ?
View SolutionA bar magnet of magnetic moment 80 units is cut into two halves of equal length, the magnetic moment of each half will be:
View SolutionCurrent is flowing in a coil of area A and number of turns N, then magnetic moment of the coil ,M is equal to
View SolutionTwo magnets of equal magnetic moments M each are placed as shown in figure below . The resultant magnetic moment is M . Then value of θ is
 View Solution
View SolutionA magnet of magnetic moment M amd pole strenth m is divided in two equal parts, then magnetic moment of each part will be
View SolutionA magnet of magnetic moment M amd pole strenth m is divided in two equal parts, then magnetic moment of each part will be
View SolutionTwo similar coils are kept mutually perpendicular such that their centres coincide. At the centre, find the ratio of the magnetic field due to one coil and the resultant magnetic field by both coils, if the same current is flown
View Solution
