Two bodies of different masses m1 and m2 have equal momenta. Their kinetic energies E1 and E2 are in the ratio
√m2m1
√m1m2
m1m2
m2m1
The correct Answer is:D
To solve the problem, we need to establish the relationship between the kinetic energies of two bodies with equal momentum. Let's denote the two bodies as Body 1 with mass m1 and Body 2 with mass m2.
Step 1: Understand the relationship between momentum and kinetic energy
The momentum p of an object is given by the formula:
p=mv
where m is the mass and v is the velocity of the object.
The kinetic energy E of an object is given by the formula:
E=12mv2
Step 2: Express velocity in terms of momentum
From the momentum formula, we can express the velocity v as:
v=pm
Step 3: Substitute the expression for velocity into the kinetic energy formula
Substituting v into the kinetic energy formula gives:
E=12m(pm)2
This simplifies to:
E=12m⋅p2m2=p22m
Step 4: Write the kinetic energies for both bodies
For Body 1:
E1=p22m1
For Body 2:
E2=p22m2
Step 5: Find the ratio of the kinetic energies
Now, we can find the ratio of the kinetic energies E1 and E2:
E1E2=p22m1p22m2=m2m1
Step 6: Conclusion
Thus, the ratio of the kinetic energies E1 and E2 is:
E1E2=m2m1
This implies that the kinetic energies are inversely proportional to their respective masses when the momentum is constant.
Final Answer
The ratio of the kinetic energies E1 and E2 is:
E1E2=m2m1
The momentum p of an object is given by the formula:
p=mv
where m is the mass and v is the velocity of the object.
E=12mv2
From the momentum formula, we can express the velocity v as:
v=pm
Substituting v into the kinetic energy formula gives:
E=12m(pm)2
This simplifies to:
E=12m⋅p2m2=p22m
For Body 1:
E1=p22m1
For Body 2:
E2=p22m2
Now, we can find the ratio of the kinetic energies E1 and E2:
E1E2=p22m1p22m2=m2m1
Thus, the ratio of the kinetic energies E1 and E2 is:
E1E2=m2m1
This implies that the kinetic energies are inversely proportional to their respective masses when the momentum is constant.
The ratio of the kinetic energies E1 and E2 is:
E1E2=m2m1
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - B)
35 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - C)
80 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - EXERCISE
37 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
Two bodies of masses m1 and m2 have equal KE. Their momenta is in the ratio
View SolutionTwo bodies of mass 1kgand2kg have equal momentum. The ratio of their kinetic energies is:
View SolutionTwo bodies of masses m1andm2 have same kinetic energy. The ratio of their momentum is
View SolutionTwo bodies of masses m1andm2(<m1) are connected to the ends of a massless cord and allowed to move as shown in figure. The pulley is both massless and frictionless. The acceleration of the centre of mass is (m1−m2)n(m1+m2)2g. Find the value of n.
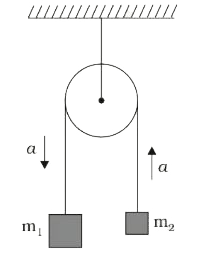
View SolutionTwo bodies with masses m1kgandm2kg have equal kinetic energies. If p1andP2 are their respective momenta, then p1/P2 is equal to :
View SolutionTwo bodies with moment of inertia l1 and l2 (l1>l2) have equal angular momentum. If E1 and E2 are the rotational kinetic energies, then
View SolutionTwo bodies with moment of inertia I1 and I2(I1>I2) have equal angular momenta. If their kinetic energy of rotation are E1 and E2 respectively, then.
View SolutionTwo particles of masses m and 2m have equal kinetic energies. Their de Broglie wavelengths area in the ratio of:
View SolutionA stationary particle explodes into two particle of a masses m1andm2 which move in opposite direction with velocities v1andv2. The ratio of their kinetic energies E1/E2 is
View SolutionTwo masses of 1 g and 4g are moving with equal linear momenta. The ratio of their kinetic energies is :
View Solution