The blades of a windmill sweep out a circle of area A. If the wind flows at a velocity v perpendicular to the circle, then the mass of the air of density ρ passing through it in time t is
ρAv32
ρAv22
ρAv2
2ρAv2
The correct Answer is:A
Step by step video & image solution for The blades of a windmill sweep out a circle of area A. If the wind flows at a velocity v perpendicular to the circle, then the mass of the air of density rho passing through it in time t is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTE ENGLISHChapter:WORK, ENERGY AND POWERExercise:Assignment (SECTION - B)
Explore 35 Videos
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTE ENGLISHChapter:WORK, ENERGY AND POWERExercise:Assignment (SECTION - C)
Explore 80 Videos
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTE ENGLISHChapter:WORK, ENERGY AND POWERExercise:EXERCISE
Explore 37 Videos
- WAVESBook:AAKASH INSTITUTE ENGLISHChapter:WAVESExercise:ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
Explore 12 Videos
Similar Questions
The blades of a windmill sweep out a circle of area A. (a) If the wind flows at a velocity v perpendicular to the circle, what is the mass of the air passing through in time t? (b) What is the kinetic energy of the air? (c) Assume that the windmill converts 25% of the wind's energy into electrical energy, and that A=30m2, v=36kmh−1 and the density of air is 1.2kgm−3, what is the electrical power produced?
View SolutionThe blades of a windmill sweep out a circle of area A. (a) If the wind flows at a velocity v perpendicular to the circle, what is the mass of the air passing through in time t? (b) What is the kinetic energy of the air? (c) Assume that the windmill converts 25% of the wind's energy into electrical energy, and that A=30m2, v=36kmh−1 and the density of air is 1.2kgm−3, what is the electrical power produced?
View SolutionA loop of flexible conducting wire of length 0.5 m lies in a magnetic field of 1.0 T perpendicular to the plane of the loop. Show that when a current as shown in Fig. 1.112 is passed through the loop, it opens into a circle. Also calculate the tension developed in the wire if the current is 1.57 A.

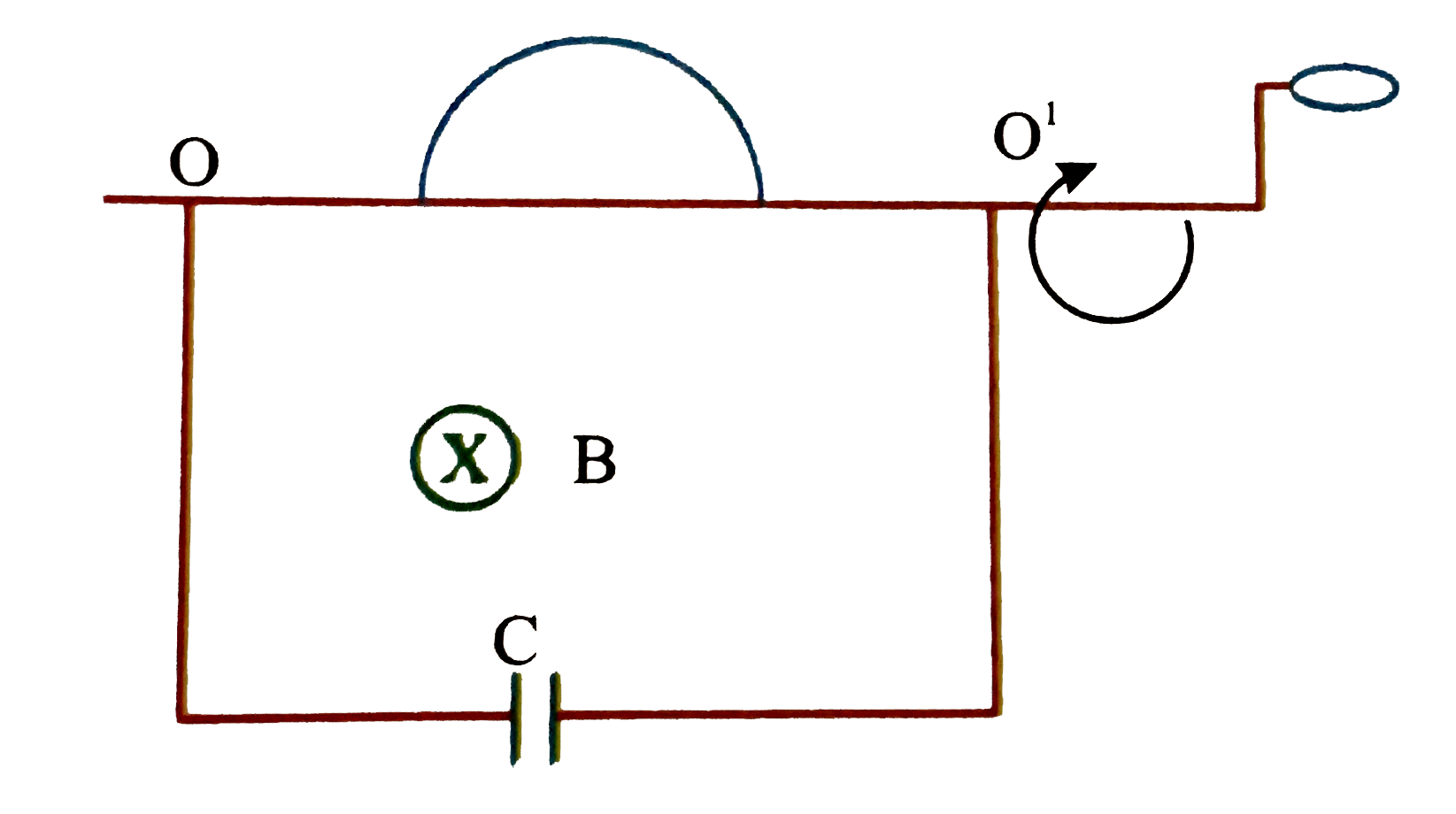
View SolutionA copper rod is bent inot a semi-circle of radius a and at ends straight parts are bent along diameter of the semi-circle and are passed through fixed, smooth and conducting ring O and O' as shown in figure. A capacitor having capacitance C is connected to the rings. The system is located in a uniform magnetic field of induction B such that axis of rotation OO' is perpendicular to the field direction. At initial moment of time (t=0), plane of semi-circle was normal to the field direction and the semi-circle is set in rotation with constant angular velocity ω. Neglect the resistance and inductance of the circuit. The current flowing through the circuit as function of time is
View SolutionThe surface density (mass/area) of a circular disc of radius a depends on the distance from the centre as ρ(r)=A+Br. Find its moment of inertia about the line perpendicular to the plane of the disc through its centre.
View SolutionThe surface density (mass/area) of a circular disc of radius a depends on the distance from the centre as ρ(r)=A+Br. Find its moment of inertia about the line perpendicular to the plane of the disc through its centre.
View SolutionA pump is designed as a horizontal cylinder with a piston of area A and and outlet orifice of area a arranged near the cylinder axis. Find the velocity of out flow of the liquid from the pump if the piston moves with a constant velocity under the action of a constant force F. The density of the liquid is ρ.
View SolutionFigure shows a mass m placed on a frictionless horizontal table and attached toa string passing through a mall hole in the surface. Initially, themas movesin a circle of radius r0 with a speed v0 and the ree end of the string is held by a person. The person pulls on the string slowly to decrease the radius of th circle of r. a. Find the tension in the string when the mass moves in the circle of radius r. b. Calculate the chasnge in the kinetic energy of the mass
View SolutionA thin circular plate of mass M and radius R has its density varying as ρ(r)=ρ0r with ρ0 as constant and r is the distance from its center. The moment of Inertia of the circular plate about an axis perpendicular to the plate and passing through its edge is I=aMR2 The value of the coefficient a is :
View SolutionA conducting rod of mass m and length l is placed over a smooth horizontal surface. A uniform magnetic field B is acting perpendicular to the rod. Charge q is suddenly passed through the rod and it acquires an initial velocity v on the surface, then q is equal to
View Solution