Two balls of masses m each are moving at right angle to each other with velocities 6 m/s and 8 m/s respectively. If collision between them is perfectly inelastic, the velocity of combined mass is
15 m/s
10m/s
5 m/s
2.5 m/s
The correct Answer is:C
To solve the problem step by step, we will use the principle of conservation of momentum.
Step 1: Define the velocities and directions
Let:
- Ball A has a mass m and is moving with a velocity of 6m/s in the x-direction. We can represent this as:
→VA=6^im/s
- Ball B has a mass m and is moving with a velocity of 8m/s in the y-direction. We can represent this as:
→VB=8^jm/s
Step 2: Write the momentum before the collision
The total momentum before the collision can be calculated as:
→Pinitial=m→VA+m→VB=m(6^i)+m(8^j)=m(6^i+8^j)
Step 3: Combine the masses after the collision
Since the collision is perfectly inelastic, both balls stick together after the collision. The combined mass is:
Mcombined=m+m=2m
Step 4: Write the momentum after the collision
Let the final velocity of the combined mass be →V. The momentum after the collision is:
→Pfinal=(2m)→V
Step 5: Apply conservation of momentum
According to the conservation of momentum:
→Pinitial=→Pfinal
This gives us:
m(6^i+8^j)=(2m)→V
Step 6: Simplify the equation
We can divide both sides by m (assuming m≠0):
6^i+8^j=2→V
Step 7: Solve for →V
Now, divide both sides by 2 to find →V:
→V=3^i+4^j
Step 8: Calculate the magnitude of the final velocity
The magnitude of the velocity V can be calculated using the Pythagorean theorem:
|→V|=√(3)2+(4)2=√9+16=√25=5m/s
Final Answer
The final velocity of the combined mass after the perfectly inelastic collision is:
5m/s
Let:
- Ball A has a mass m and is moving with a velocity of 6m/s in the x-direction. We can represent this as:
→VA=6^im/s
- Ball B has a mass m and is moving with a velocity of 8m/s in the y-direction. We can represent this as:
→VB=8^jm/s
The total momentum before the collision can be calculated as:
→Pinitial=m→VA+m→VB=m(6^i)+m(8^j)=m(6^i+8^j)
Since the collision is perfectly inelastic, both balls stick together after the collision. The combined mass is:
Mcombined=m+m=2m
Let the final velocity of the combined mass be →V. The momentum after the collision is:
→Pfinal=(2m)→V
According to the conservation of momentum:
→Pinitial=→Pfinal
This gives us:
m(6^i+8^j)=(2m)→V
We can divide both sides by m (assuming m≠0):
6^i+8^j=2→V
Now, divide both sides by 2 to find →V:
→V=3^i+4^j
The magnitude of the velocity V can be calculated using the Pythagorean theorem:
|→V|=√(3)2+(4)2=√9+16=√25=5m/s
The final velocity of the combined mass after the perfectly inelastic collision is:
5m/s
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - C)
80 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - D)
13 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - A)
64 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
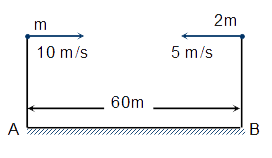
Two particles, one of mass m and the other of mass 2m, are projected horizontally towards each other from the same level above the ground with velocities 10 m/s and 5 m/s, respectively. They collide in air and stick to each other. The distance of the combined mass from point A is
View SolutionTwo identical balls each of mass 4 kg are moving towards each other with speeds 2 m/s and 3 m/s respectively. They undergo head on perfectly elastic collision. Then impulse imparted by one ball on other is
View SolutionTwo particles A and B of equal size but of masses mkg and 2mkg are moving directly towards each other with speeds 21m/s and 4m/s respectively. After collision, A moves with a speed of 1m/s in the original direction. Then:
View SolutionTwo balls of masses 2kg and 4kg are moved towards each other with velocities 4m/s and 2m/s, respectively, on a frictionless surface. After colliding, the 2kg ball returns back with velocity 2m/s. then find
a. velocity of the 4kg after collision
b. coefficient of restitution e,
c. impulse of deformation JD
d. maximum potential energy of deformation,
e. impulse of reformation JR
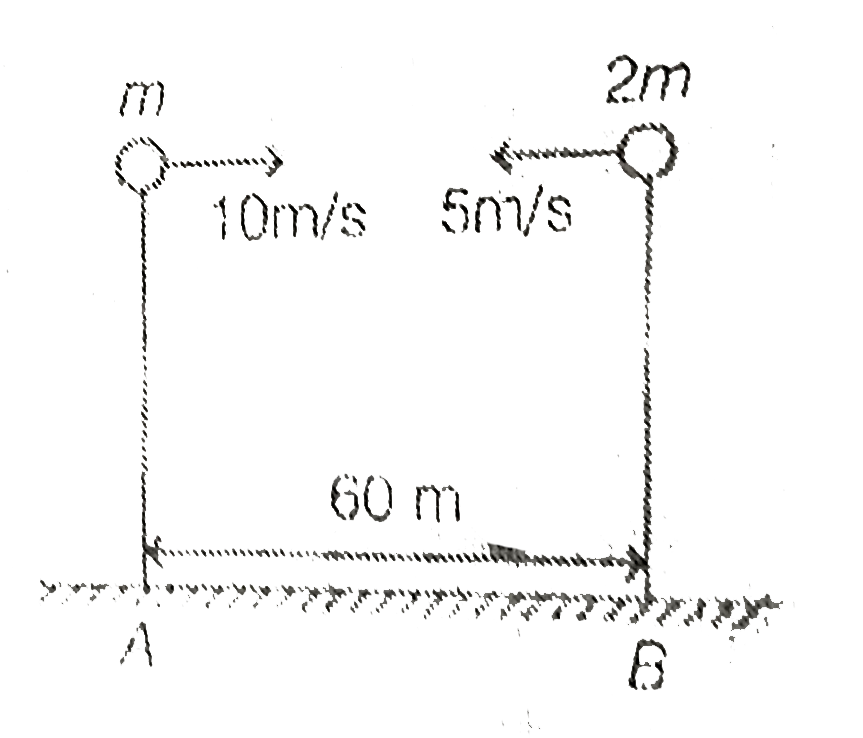
View SolutionTwo particles one of mass m and the other of mass 2 m are projected horizontally towards each other from the same level above the ground with velocities 10 m/s and 5 m/s respectively . They collide in air and stick to each other . The distance from A , where the combined mass finally land is
View SolutionTwo steel balls A and B of mass 10 kg and 10 g rolls towards each other with 5m/s and 1 m/s respectively on a smooth floor. After collision, with what speed B moves [perfectly elastic collision]?
View SolutionTwo equal masses m1 and m2 moving along the same straight line with velocites +3m/s and −5m/s respectively collide elastically. Their velocities after the collision will be respectively.
View SolutionTwo equal masses m1 and m2 moving along the same straight line with velocites +3m/s and −5m/s respectively collide elastically. Their velocities after the collision will be respectively.
View SolutionA body of mass m is dropped from a height of h. Simultaneously another body of mass 2m is thrown up vertically with such a velocity v that they collide at height h2. If the collision is perfectly inelastic, the velocity of combined mass at the time of collision with the ground will be
View SolutionA body of mass m is dropped from a height of h. Simultaneously another body of mass 2m is thrown up vertically with such a velocity v that they collide at height h2. If the collision is perfectly inelastic, the velocity of combined mass at the time of collision with the ground will be
View Solution
