A proton is fixed at origin. Another proton is released from rest, from a point at a distance from origin. Taking charge of portion as e and mass as , find the speed of the proton (i) at a distance from origin (ii) at large distance from origin.
The proton moves away under electrostatic repulsion,
As there is no extemal force,
KE + PE= 0
(i)
(ii)
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - EXERCISE
20 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - A
44 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-J Aakash Challengers Questions
5 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
Similar Questions
When E⊥B and the particle is released at rest from origin.
View SolutionFind the distance from the origin to each of the point:
(4,−1,2)
View SolutionFind the distance from the origin to each of the point:
(2,2,3)
View SolutionFind the distance from the origin to (6,6,7).
View SolutionFind the locus of point whose distance from the origin is 5.
View SolutionFind the distance from the origin to each of the point:
(0,4,−4)
View Solution4 charges are placed each at a distance a from origin . The dipole moment of configuration is .
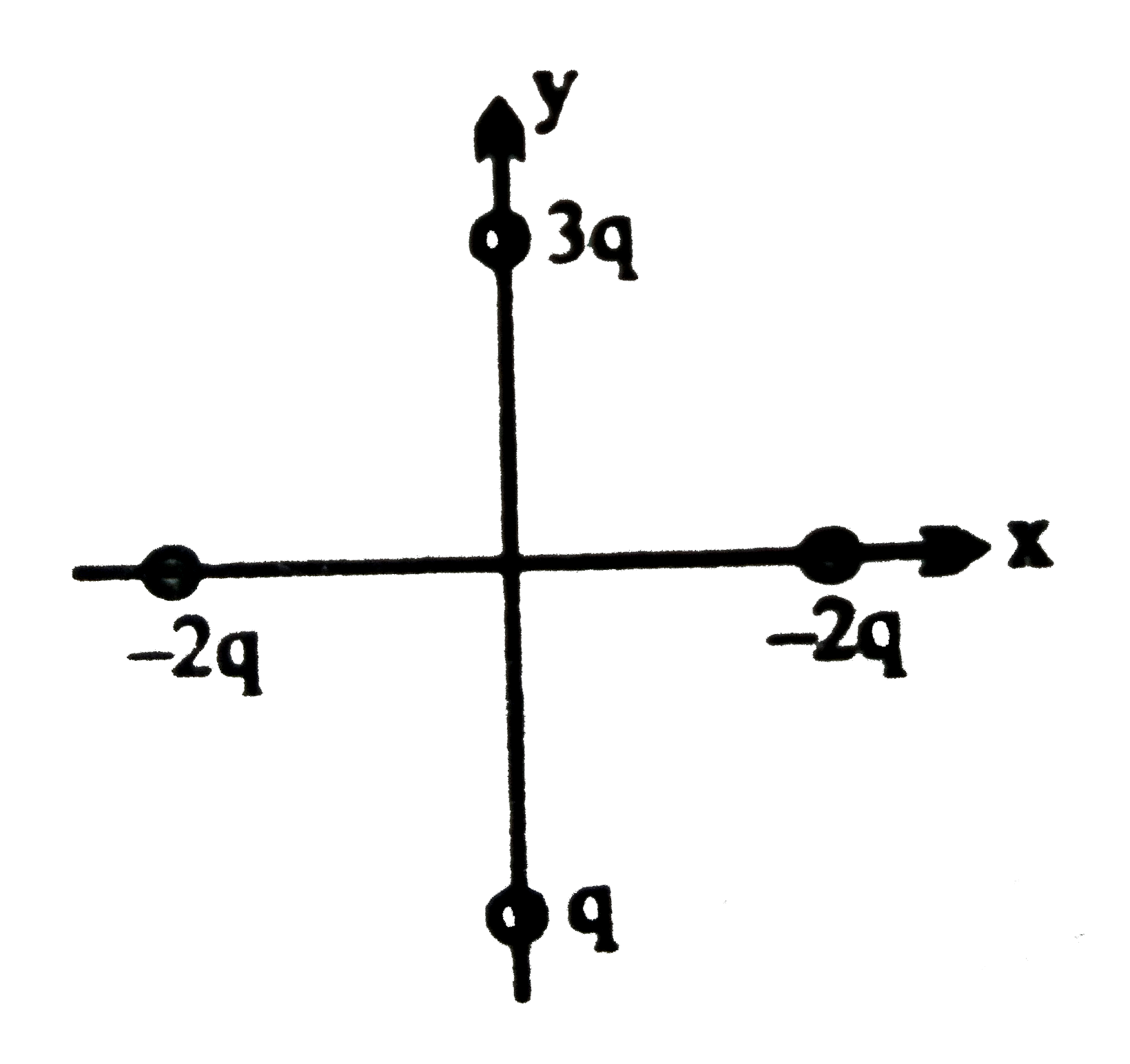 .
.
View SolutionAll the particles of a body situated at distance R from the origin. The distance of the center of mass of the body from the origin is
View SolutionFind the distance from the origin to each of the point:
(−4,−3,−2)
View SolutionA positive charge is released from rest at a distance r0 from a positive line charge with uniform density . The speed (v) of the point charge , as a function of instantaneous distance r from line charge, is proportional to:
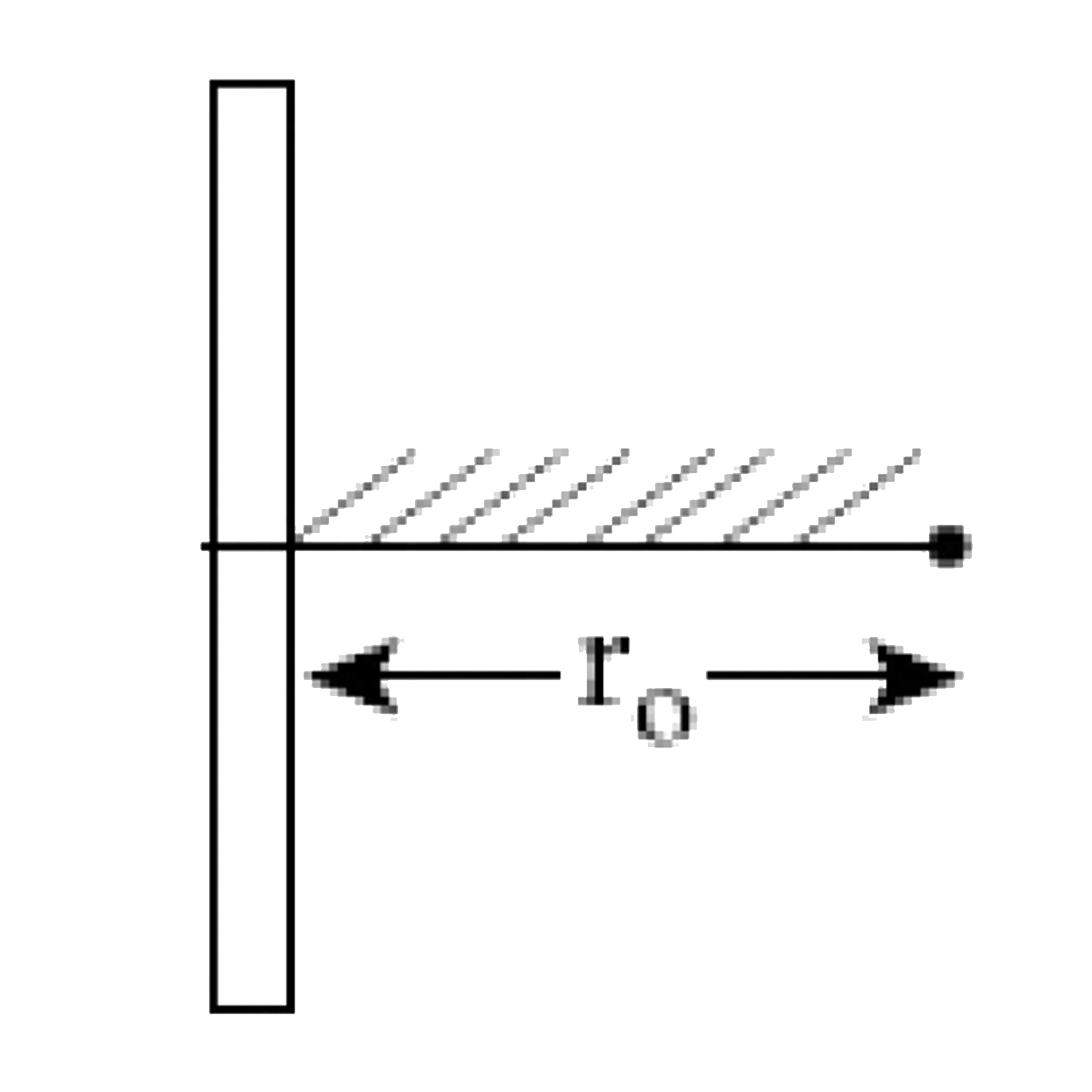
View Solution
