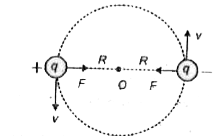
Two charges, $+ q$ and -q, each of mass m , are revolving in a circle of radius R, under mutual electrostatic force. Find (i) speed of each charge (ii) kinetic energy of system (iii) potential energy of the system (iv) total energy of the system.

Video Solution

Text Solution

Verified by Experts

In this situation, the centripetal force is provided by he electrostatic force of attraction
(i) By newton's second law, F = $\frac{1}{4 π ε_{0}} \frac{q^{2}}{{(2 R)}^{2}} = \frac{m v^{2}}{R}$
$\Rightarrow v = \sqrt{\frac{1}{4 π ε_{0}} \frac{q^{2}}{(4 R) m}}$
(ii) Kinetic energy of the system = $\frac{1}{2} m v^{2} + \frac{1}{2} m v^{2} = \frac{q^{2}}{4 π ε_{0} (4 R)} = \frac{q^{2}}{16 π ε_{0} R}$
(iii) Potential energy of the system = $\frac{1}{4 π ε_{0}} \frac{q (- q)}{2 R} = \frac{- 1}{4 π ε_{0}} \frac{q^{2}}{(2 R)} = \frac{- q^{2}}{8 π ε_{0} R}$
(iv) Total energy of the system = K.E + P.e = $\frac{- q^{2}}{4 π ε_{0} (4 R)} = \frac{- q^{2}}{16 π ε_{0} R}$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Similar Questions

AAKASH INSTITUTE ENGLISH-ELECTROSTATIC POTENTIAL AND CAPACITANCE -EXAMPLE

Home
Ask Doubt
Profile