A point P on the trajectory of a projectile projected at angle with θ with horizontal subtrends angles α and β at the point of landing them
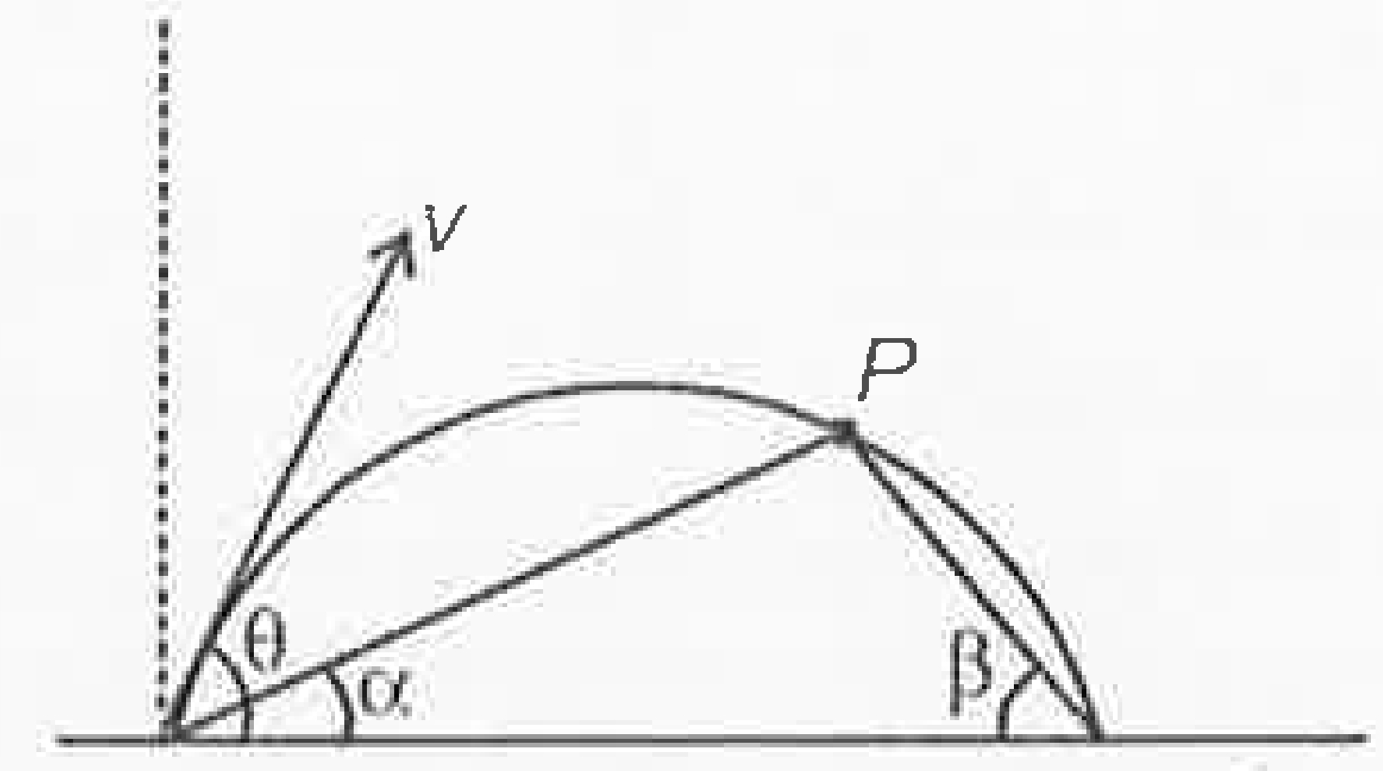
tanθ +tanα= tanβ
tanα +tanβ = tanθ
tanθ +tanβ = tanα
tanθ +tanα = 2tanβ
The correct Answer is:B
Step by step video & image solution for A point P on the trajectory of a projectile projected at angle with theta with horizontal subtrends angles alpha and beta at the point of landing them by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
If a body is projected with an angle θ to the horizontal, then
Aits velocity is always perpendicular to its acceleration thenBits velocity becomes zero at its maximum height.Cits velocity makes zero angle with the horizontal at its maximum height.Dthe body just before hitting the ground, the direction of velocity coincides with the acceleration.Galileo writes that for angles of projection of a projectile at angles (45+θ) and (45−θ), the horizontal ranges described by the projectile are in the ratio of (if θ≤45)
A2:1B1:2C1:1D2:3
A particle is projected with speed u at angle θ to the horizontal. Find the radius of curvature at highest point of its trajectory
View SolutionA particle of mass m is projected with velocity v at an angle θ with the horizontal. Find its angular momentum about the point of projection when it is at the highest point of its trajectory.
View SolutionA body of mass m is projected with a velocity u at an angle θ with the horizontal. The angular momentum of the body, about the point of projection, when it at highest point on its trajectory is
View SolutionFor angles of projection of a projectile at angle (45∘−θ)and(45∘+θ), the horizontal ranges described by the projectile are in the ratio of :
View SolutionFor angles of projection of a projectile at angle (45∘−θ)and(45∘+θ), the horizontal ranges described by the projectile are in the ratio of :
View SolutionWhat is the radius of curvature of the parabola traced out by the projectile in which a particle is projected with a speed u at an angle θ with the horizontal, at a point where the velocity of particle makes an angle θ/2 with the horizontal.
View Solution
