In meter bridge experiment if, resistance S in resistance box =300Ω then the balanced length is found to be 25.0cm from end A. The diameter of unknown wire is 1mm and length of unknown wire is 31.4cm. The specific resistivity of the wire should be
2.5×10−4Ω−m
3.5×10−4Ω−m
4.5×10−4Ω−m
None of these
The correct Answer is:A
To find the specific resistivity of the unknown wire in the meter bridge experiment, we can follow these steps:
1. Identify Given Values:
- Resistance S=300Ω
- Balanced length from end A (let's call it L1) = 25.0 cm
- Length of the unknown wire L=31.4cm
- Diameter of the wire d=1mm=0.1cm
2. Calculate the Remaining Length:
- The total length of the meter bridge wire is 100 cm. Therefore, the length from end B (let's call it L2) is:
L2=100cm−L1=100cm−25.0cm=75.0cm
3. Use the Meter Bridge Formula:
- According to the meter bridge principle:
SR=L2L1
- Plugging in the values:
300ΩR=75.0cm25.0cm
- Simplifying the right side:
300ΩR=3
- Therefore, solving for R:
R=300Ω3=100Ω
4. Calculate the Cross-Sectional Area A of the Wire:
- The area A of a circular wire is given by:
A=π(d2)2
- Substituting the diameter:
A=π(0.1cm2)2=π(0.05cm)2=π×0.0025cm2
- Converting to square meters:
A=π×0.0025×10−4m2=π×2.5×10−6m2
5. Calculate the Specific Resistivity ρ:
- The formula for resistance is:
R=ρLA
- Rearranging for ρ:
ρ=R⋅AL
- Substituting the known values:
ρ=100Ω⋅(π×2.5×10−6m2)31.4×10−2m
- Simplifying:
ρ=100⋅3.14⋅2.5×10−60.314≈785×10−60.314≈2.5×10−4Ω⋅m
Final Result:
The specific resistivity of the wire is approximately:
ρ≈2.5×10−4Ω⋅m
- Resistance S=300Ω
- Balanced length from end A (let's call it L1) = 25.0 cm
- Length of the unknown wire L=31.4cm
- Diameter of the wire d=1mm=0.1cm
- The total length of the meter bridge wire is 100 cm. Therefore, the length from end B (let's call it L2) is:
L2=100cm−L1=100cm−25.0cm=75.0cm
- According to the meter bridge principle:
SR=L2L1
- Plugging in the values:
300ΩR=75.0cm25.0cm
- Simplifying the right side:
300ΩR=3
- Therefore, solving for R:
R=300Ω3=100Ω
- The area A of a circular wire is given by:
A=π(d2)2
- Substituting the diameter:
A=π(0.1cm2)2=π(0.05cm)2=π×0.0025cm2
- Converting to square meters:
A=π×0.0025×10−4m2=π×2.5×10−6m2
- The formula for resistance is:
R=ρLA
- Rearranging for ρ:
ρ=R⋅AL
- Substituting the known values:
ρ=100Ω⋅(π×2.5×10−6m2)31.4×10−2m
- Simplifying:
ρ=100⋅3.14⋅2.5×10−60.314≈785×10−60.314≈2.5×10−4Ω⋅m
The specific resistivity of the wire is approximately:
ρ≈2.5×10−4Ω⋅m
Topper's Solved these Questions
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - MCQ_TYPE
17 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - MATCH THE COLUMN
6 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Medical entranes gallery
49 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
Similar Questions
If resistance S in RB=300Ω, then the balanced length is found to be 25.0cm from end A. The diameter of unknown wire is 1mm and length of the unknown wire is 3.14cm. The specific resistivity of the wire should be
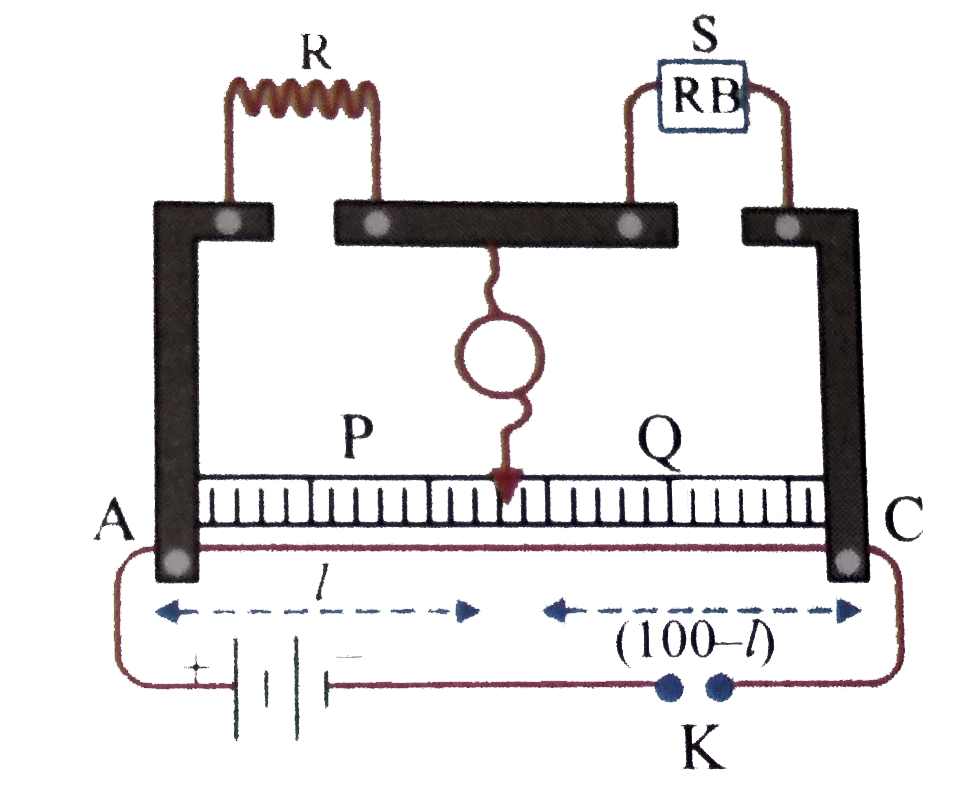
View SolutionIf resistance R1 in resistance box is 300Ω then the balanced length is found to be 75.0cm from end A. The diameter of unknown wire is 1 mm and length of the unknown wire is 31.4cm. Find the specific resistance of the unknown wire
View SolutionIf resistanceR1 in resistance box is 300Ω, then the balanced length is found to be 75.0cm from end A.The diameter of known wire is 1mm and length of the unknown wire is 31.4cm. Find the specific resistance of the unknown wire.
View SolutionIn above question if resistance of meter bridge wire is 1 Ω /cm then the value of current / is
View SolutionIf a wire is stretched to four times its length, then the specific resistance of the wire will
View SolutionIn a meter bridge, null point is at l=33.7cm, when the resistance S is shunted by 12Ω resitance the null point is found to be shifted by a distance of 18.2cm. The value of unknown resistance R should be

View Solution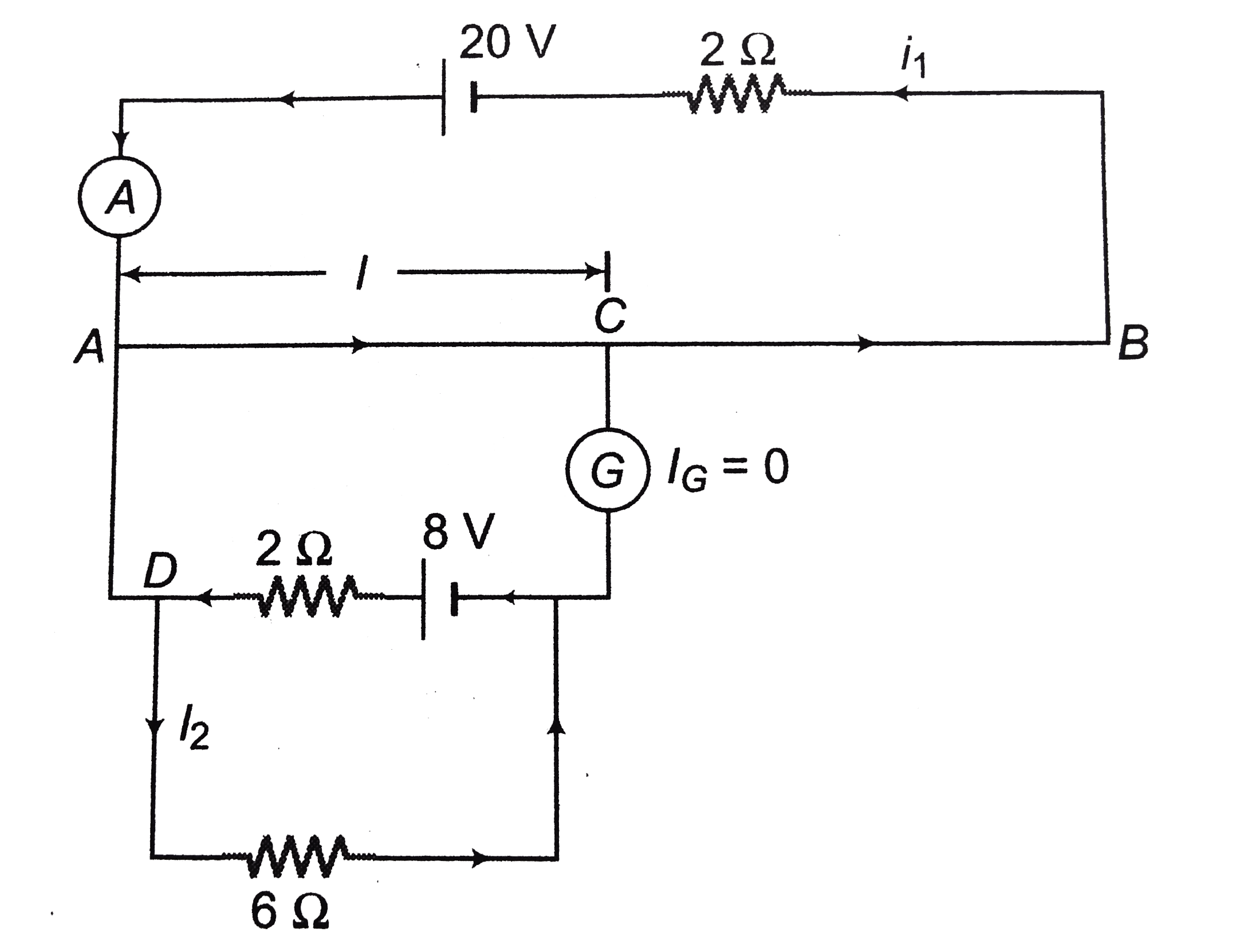
In the figure shown wire AB has a length of 100cm and resistance 8Ω. Find the balance point length l.
View SolutionIn a meter bridge, null point is 20cm, when the known resistance R is shunted by 10Ω resistance, null point is found to be shifted by 10 cm. Find the unknown resistance X.
View SolutionIn a meter bridge, null point is 20cm, when the known resistance R is shunted by 10Ω resistance, null point is found to be shifted by 10 cm. Find the unknown resistance X.
View SolutionIn meter bridge , the balancing length from left is found to be 20 cm when standard connected of 1Ω is in right gap . The value of unknown resistance is
View Solution
