The charge on the 4 uF capacitor, when a battery of 20 V is connected across points A and B in the circuit as shown in the figure is
40 muC
20 muC
10 muC
60 muC
To find the charge on the 4 µF capacitor when a 20 V battery is connected across points A and B, we can follow these steps:
1. Identify the Capacitance Values:
We have two capacitors in the circuit:
- Capacitor 1 (C1) = 4 µF
- Capacitor 2 (C2) = 12 µF
2. Understand the Voltage Relationship:
When capacitors are connected in series, the total voltage (V) across the capacitors is the sum of the voltages across each capacitor:
V=V1+V2
where V1 is the voltage across the 4 µF capacitor and V2 is the voltage across the 12 µF capacitor.
3. Use the Formula for Voltage Across a Capacitor:
The voltage across a capacitor can be expressed in terms of charge (Q) and capacitance (C):
V=QC
Therefore, we can write:
V1=QC1=Q4×10−6andV2=QC2=Q12×10−6
4. Set Up the Equation:
Substitute V1 and V2 into the voltage relationship:
Q4×10−6+Q12×10−6=20
5. Combine the Terms:
To combine the fractions, find a common denominator. The least common multiple of 4 and 12 is 12:
3Q12×10−6+Q12×10−6=20
This simplifies to:
4Q12×10−6=20
6. Solve for Q:
Multiply both sides by 12×10−6:
4Q=20×12×10−6
4Q=240×10−6
Divide both sides by 4:
Q=240×10−64=60×10−6
Therefore,
Q=60μC
Final Answer:
The charge on the 4 µF capacitor is 60 µC.
We have two capacitors in the circuit:
- Capacitor 1 (C1) = 4 µF
- Capacitor 2 (C2) = 12 µF
When capacitors are connected in series, the total voltage (V) across the capacitors is the sum of the voltages across each capacitor:
V=V1+V2
where V1 is the voltage across the 4 µF capacitor and V2 is the voltage across the 12 µF capacitor.
The voltage across a capacitor can be expressed in terms of charge (Q) and capacitance (C):
V=QC
Therefore, we can write:
V1=QC1=Q4×10−6andV2=QC2=Q12×10−6
Substitute V1 and V2 into the voltage relationship:
Q4×10−6+Q12×10−6=20
To combine the fractions, find a common denominator. The least common multiple of 4 and 12 is 12:
3Q12×10−6+Q12×10−6=20
This simplifies to:
4Q12×10−6=20
Multiply both sides by 12×10−6:
4Q=20×12×10−6
4Q=240×10−6
Divide both sides by 4:
Q=240×10−64=60×10−6
Therefore,
Q=60μC
The charge on the 4 µF capacitor is 60 µC.
Topper's Solved these Questions
- TEST 1BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE
21 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Try Yourself
63 Videos
- TEST 2BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 2EXERCISE - Exercise
308 Videos
Similar Questions
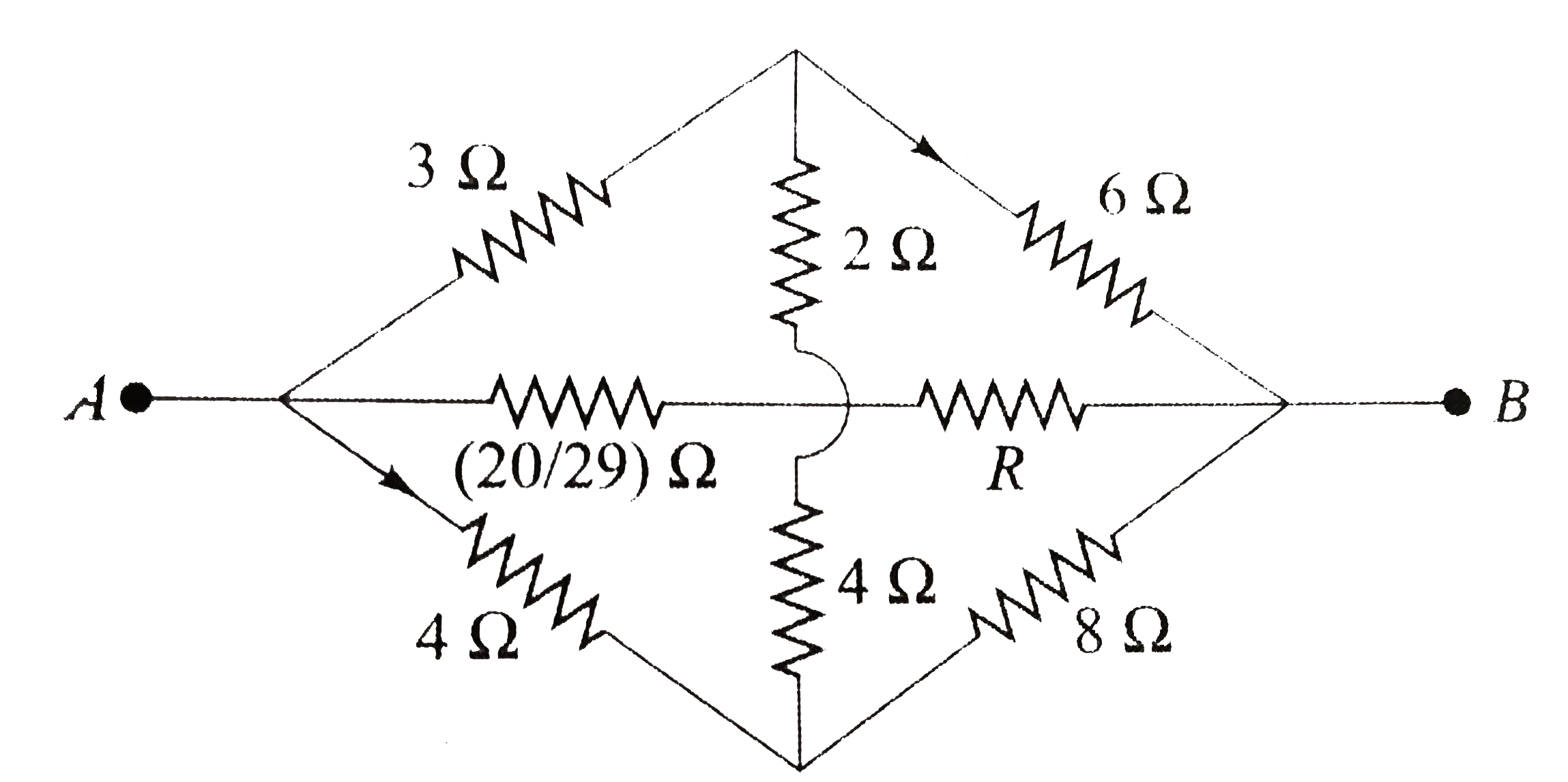
The equivalent resistance across points A and B , in the circuit shown in the figure , is
_PHY_E01_017_Q01.png)
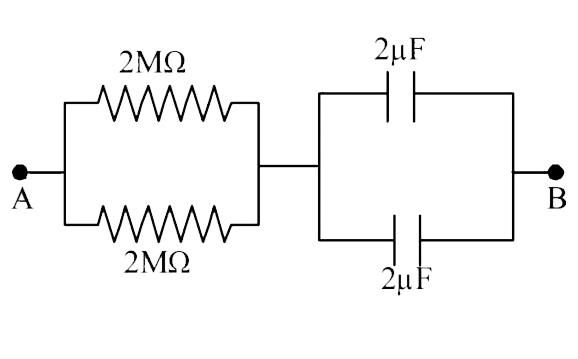
View SolutionA battery of emf 2 V and initial resistance 1Ω is
connected across terminals A and B of the circuit shown
in figure
 .
.
View SolutionAt time t=0, a battery of 10 V is connected across points A and B in the given circuit. If the capacitors have no charge initially, at what time (in seconds) does the voltage across them beocme 4V? [Take:In5=1.6,In3=1.1].
 .
.
View SolutionThe charge supplied by the battery in the circuit shown in the figure
View SolutionThe equivalent capacitance of the combination between A and B in the given Fig. is 4μF
(i) Calculate capacitance of capacitor C.
(ii) Calculate charge on each capacitor if a 12Vbattery is connected across terminals A and B.
(iii) What will be the potential drop across each capacitor ?

View SolutionCalculate the charge on each capacitor and the potential difference across it in the circuits shown in figure for the cases :
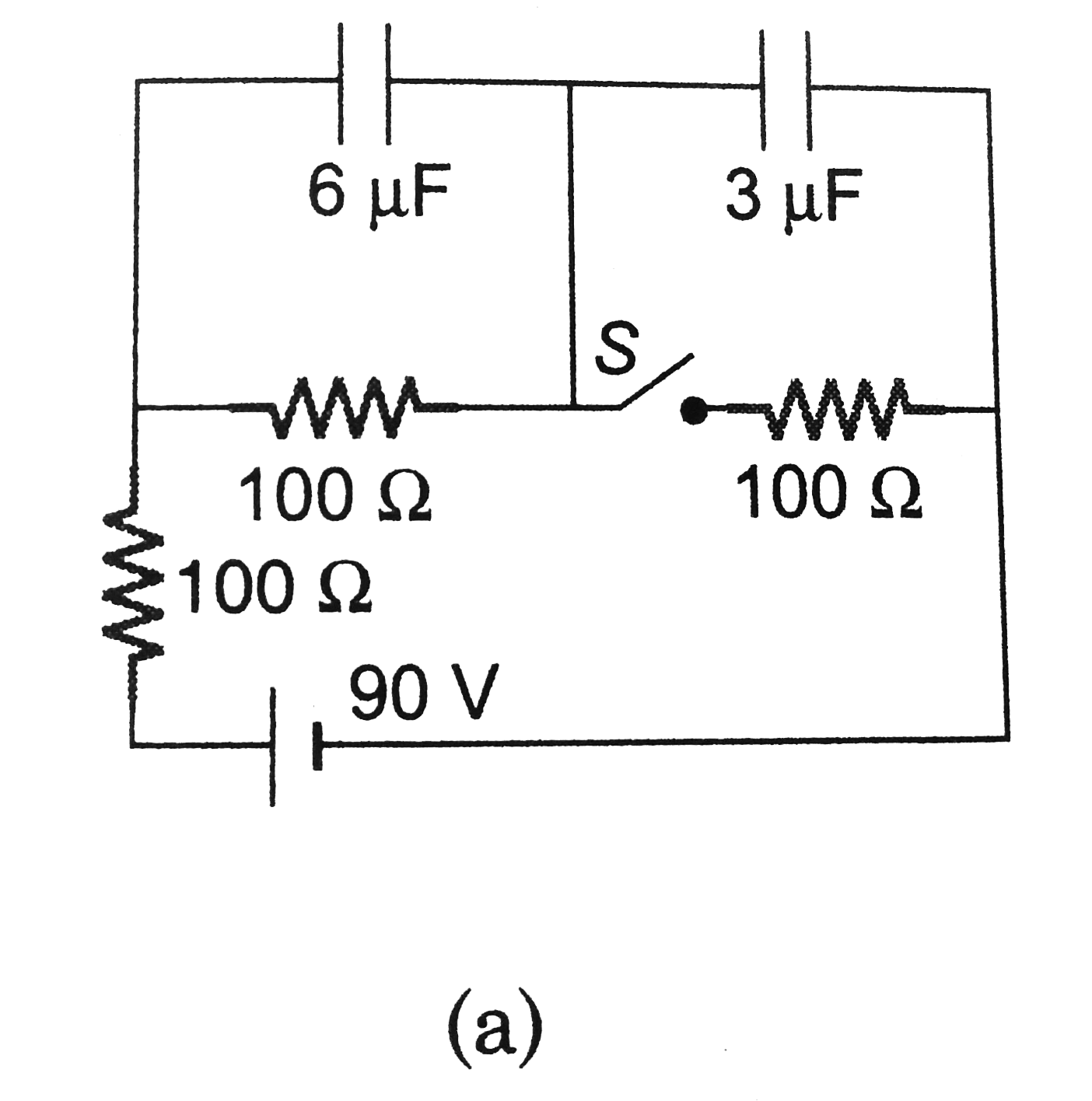
(i) switch S is closed and
(ii) switch S is open.
(iii) In. figure (b), what is the potential of point A when S is open?
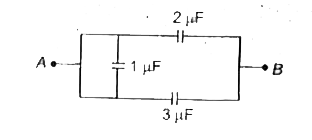
View SolutionIn the given circuit the charge on the plates of 1 μF capacitor, when 100 V battery is connected to the terminals A and B will be
View SolutionA 12 pF capacitor is connected to a 50 V battery. How much electrostatic energy is stored in the capacitor ? If another capacitor of 6 pF is connected across the combination, find the charge stored and potential difference across each capacitor.
View SolutionA 10μF capacitor is charged to 15V. It is next connected in seties with an uncharged 5μf capacitor. The series cambination is finally connected across a 30V battery, as shown in. Find the new potential differnce across the 5μF and 10μF capacitors.
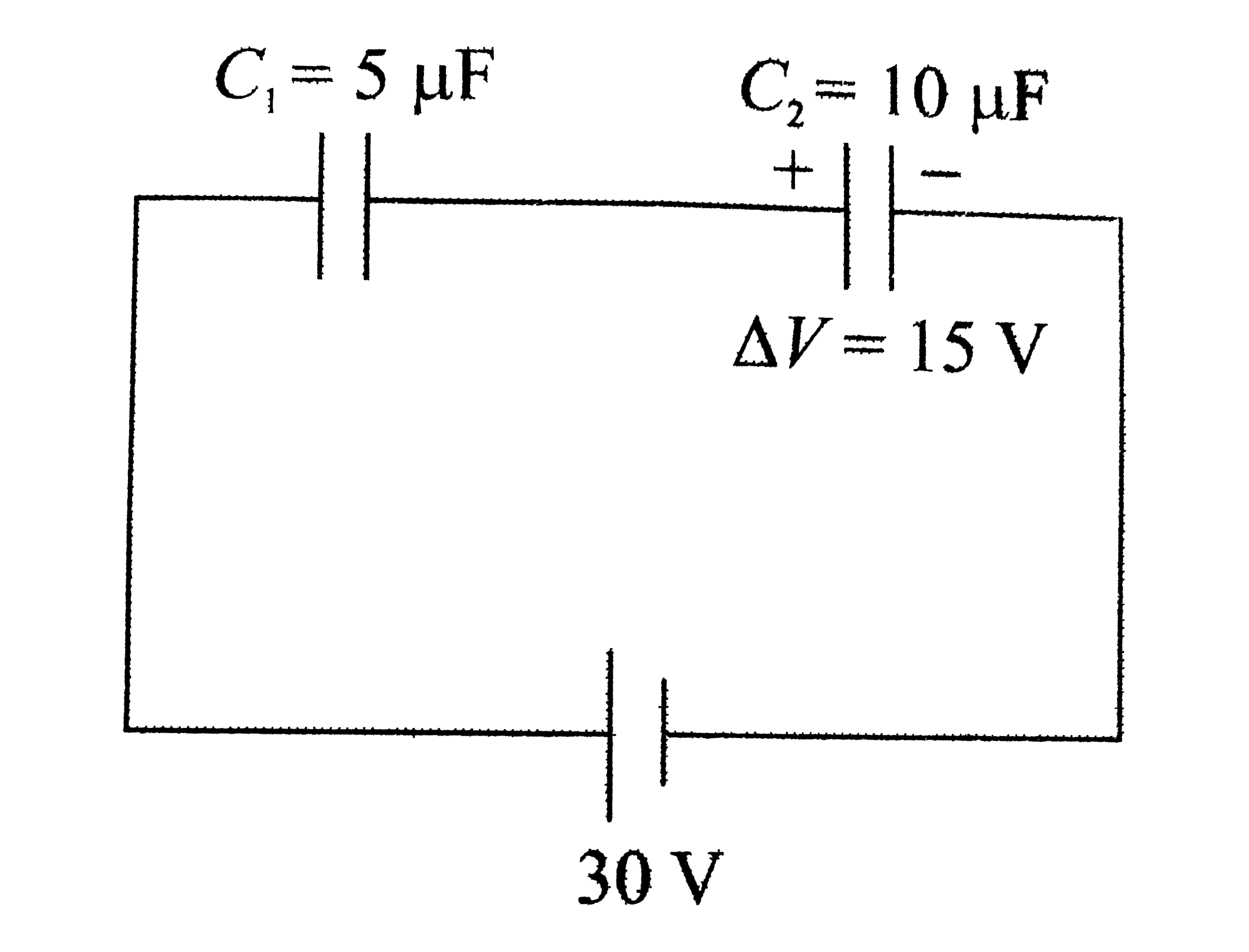
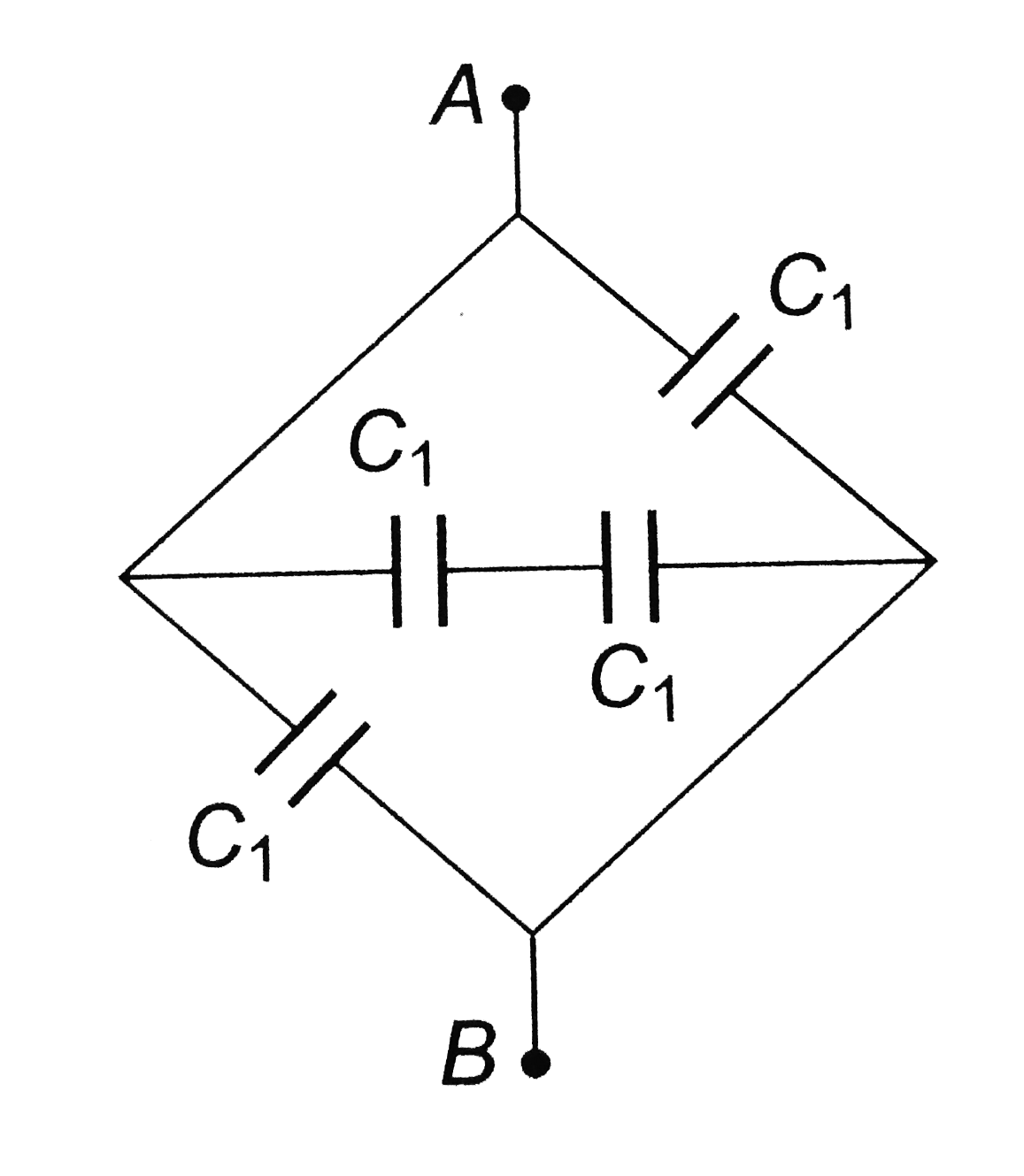
View SolutionFour identical capacitors are connected as shown in diagram. When a battery of 6V is connected between A and B, the charges stored is found to be 1.5μC. The value of C1 is
View Solution

