Two identical blocks A and B are connected with a spring of constant k as shown in ligure. If block B s moving rightward with speed V0 maximum extension of spring is
[V0{√mk}]
Zero
[V0{√2mk}]
[V0{√m2k}]
To solve the problem of finding the maximum extension of the spring when block B is moving rightward with speed V0, we can follow these steps:
Step 1: Understand the System
We have two identical blocks A and B connected by a spring with spring constant k. Block B is moving to the right with an initial speed V0. We need to find the maximum extension x of the spring when the blocks interact.
Hint: Visualize the scenario and identify the initial conditions and the forces acting on the blocks.
Step 2: Apply Conservation of Momentum
Since no external forces are acting on the system, we can apply the conservation of momentum. Before the interaction, only block B is moving with speed V0, while block A is at rest.
Initial momentum=Final momentum
Let the final velocities of blocks A and B after the interaction be VA and VB respectively. The total momentum before the interaction is:
MV0=MVA+MVB
Since the blocks are identical, we can simplify this to:
V0=VA+VB
Hint: Remember that momentum is conserved in an isolated system.
Step 3: Determine the Condition for Maximum Extension
At maximum extension, the velocities of both blocks will be equal, say Vmax. Therefore, we have:
VA=VB=Vmax
From the momentum conservation equation, we can substitute:
V0=2Vmax⟹Vmax=V02
Hint: Think about the point at which the spring is maximally extended—both blocks will move together momentarily.
Step 4: Calculate the Kinetic Energy
The total kinetic energy of the system before the interaction is given by:
KEinitial=12MV20
At maximum extension, the kinetic energy of both blocks will be:
KEfinal=2(12MV2max)=MV2max
Substituting Vmax=V02:
KEfinal=M(V02)2=MV204
Hint: Kinetic energy is converted to potential energy in the spring as it stretches.
Step 5: Relate Kinetic Energy to Potential Energy
The potential energy stored in the spring at maximum extension is given by:
PE=12kx2
At maximum extension, the kinetic energy lost by the system is equal to the potential energy stored in the spring:
KEinitial−KEfinal=PE
Substituting the values we found:
12MV20−MV204=12kx2
This simplifies to:
14MV20=12kx2
Hint: Set the kinetic energy difference equal to the potential energy to find x.
Step 6: Solve for Maximum Extension x
Rearranging the equation gives:
x2=MV202k
Taking the square root:
x=V0√M2k
Hint: Ensure to check the units for consistency when deriving the final expression.
Final Answer
The maximum extension of the spring is:
x=V0√M2k
We have two identical blocks A and B connected by a spring with spring constant k. Block B is moving to the right with an initial speed V0. We need to find the maximum extension x of the spring when the blocks interact.
Since no external forces are acting on the system, we can apply the conservation of momentum. Before the interaction, only block B is moving with speed V0, while block A is at rest.
At maximum extension, the velocities of both blocks will be equal, say Vmax. Therefore, we have:
The total kinetic energy of the system before the interaction is given by:
The potential energy stored in the spring at maximum extension is given by:
Rearranging the equation gives:
The maximum extension of the spring is:
Topper's Solved these Questions
Similar Questions
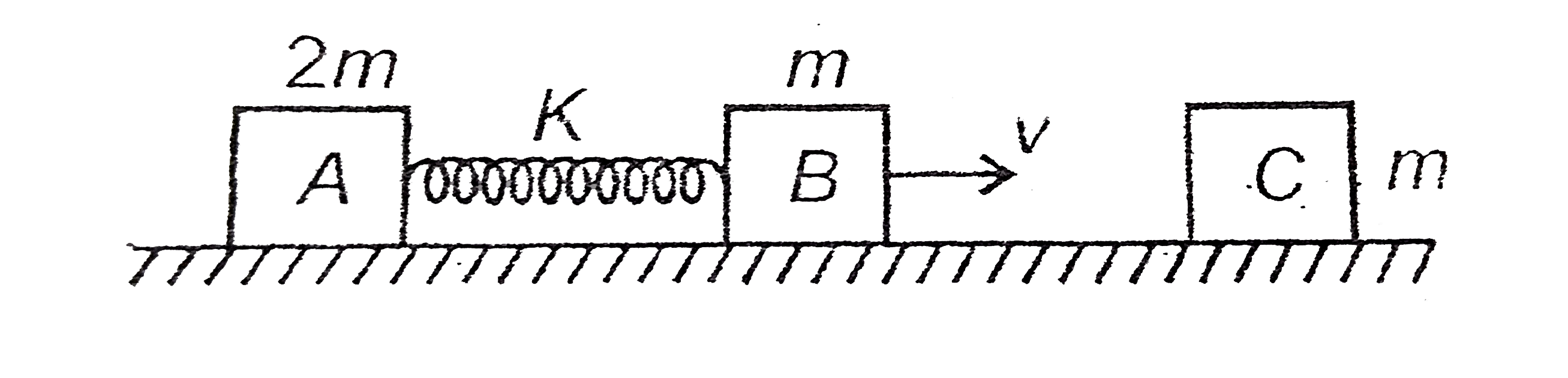
Two blocks A and B of mass 2m and m respectively are connected to a massless spring of force constant K as shown in figure A and B are moving on the horizontal frcitionless surface with velocity v to right with underformed spring. If B collides with C elastically, then maximum compression of the spring will be
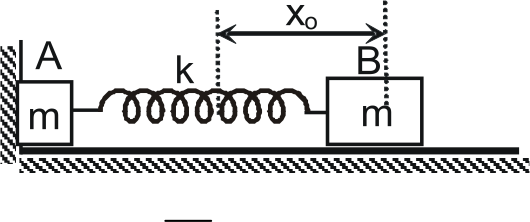
View SolutionTwo identical blocks A and B of mass m each are connected to each other by spring of spring constant k. Block B is initially shifted to a small distance x0 to the left and then released. Choose the correct statements for this problem, after the spring attains it's natural length.
View SolutionTwo identical massless springs A and B consist spring constant kA and kB respectively. Then :
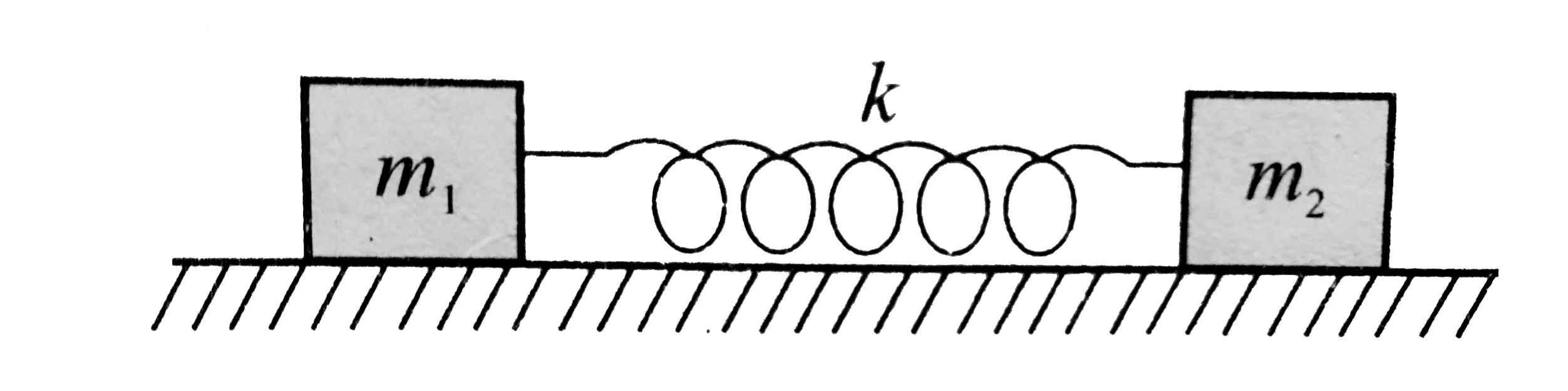
View SolutionTwo blocks m1 and m2 are pulled on a smooth horizontal surface, and are joined together with a spring of stiffness k as shown in Fig. Suddenly, block m2 receives a horizontal velocity v0, then the maximum extension xm in the spring is
View SolutionIf both the blocks moving with constant accelerattion then extension in spring.
View SolutionA block of mass 20 kg is hung with the help of ideal string, pulleys and spring (Spring constant k = 1000 N/m) as shown in figure. If block is in equilibrium position then extension in the spring will be (g=10ms−2)
View SolutionA 2 kg block is connected with two springs of force constants k1=100N/m and k2=300N/m as shown in figure. The block is released from rest with the springs unstretched. The acceleration of the block in its lowest postion is (g=10m/s2)

View SolutionTwo blocks A and B. each of mass m, are connected by a massless spring of natural length I. and spring constant K. The blocks are initially resting in a smooth horizontal floor with the spring at its natural length, as shown in Fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B. and collides elastically with A. Then

View SolutionA constant force produces maximum velocity V on the block connected to the spring of force constant K as shown in the figure. When the force constant of spring becomes 4K, the maximum velocity of the block is

View SolutionA block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is upstretched when a constant force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View Solution
