In the given resonating circuit the reading of voltmeter V is 314 volt. The value of inductance L and resistance R respectively will be about
1H,220Ω
0.1H,200Ω
1H,100Ω
0.001H2kΩ
To solve the problem, we need to find the values of inductance L and resistance R in a resonating circuit where the voltmeter reading VL is given as 314 volts. The circuit is supplied with a voltage of 220 volts at a frequency of 50 Hz.
1. Identify the given values:
- Voltmeter reading, VL=314V
- Supply voltage, V=220V
- Frequency, f=50Hz
2. Understand the relationship in the resonating circuit:
- In a resonating circuit, the voltage across the inductor VL can be expressed as:
VL=I⋅XL
- Where I is the current and XL is the inductive reactance given by:
XL=ωL=2πfL
3. Calculate the current I:
- The current I can be calculated using Ohm's law:
I=VR
- Substituting this into the equation for VL:
VL=VR⋅XL
- Rearranging gives:
R=V⋅XLVL
4. Calculate the inductive reactance XL:
- We know VL=314V and V=220V:
R=220⋅XL314
5. Find the value of R:
- To find XL, we need to express it in terms of R:
XL=314R220
6. Substituting XL back into the equation:
- We know XL=2πfL:
2π(50)L=314R220
7. Calculate the resistance R:
- From the previous steps, we can assume R is approximately 220 ohms based on the given values.
8. Calculate the inductance L:
- Rearranging the equation for L:
L=XL2πf
- Substitute XL=2π(50)R:
L=3142π(50)
- This simplifies to:
L=1H
Final Values:
- The resistance R is approximately 220Ω.
- The inductance L is approximately 1H.
- Voltmeter reading, VL=314V
- Supply voltage, V=220V
- Frequency, f=50Hz
- In a resonating circuit, the voltage across the inductor VL can be expressed as:
VL=I⋅XL
- Where I is the current and XL is the inductive reactance given by:
XL=ωL=2πfL
- The current I can be calculated using Ohm's law:
I=VR
- Substituting this into the equation for VL:
VL=VR⋅XL
- Rearranging gives:
R=V⋅XLVL
- We know VL=314V and V=220V:
R=220⋅XL314
- To find XL, we need to express it in terms of R:
XL=314R220
- We know XL=2πfL:
2π(50)L=314R220
- From the previous steps, we can assume R is approximately 220 ohms based on the given values.
- Rearranging the equation for L:
L=XL2πf
- Substitute XL=2π(50)R:
L=3142π(50)
- This simplifies to:
L=1H
- The resistance R is approximately 220Ω.
- The inductance L is approximately 1H.
Topper's Solved these Questions
Similar Questions
In the circuit shown below. The reading of the voltmeter V is
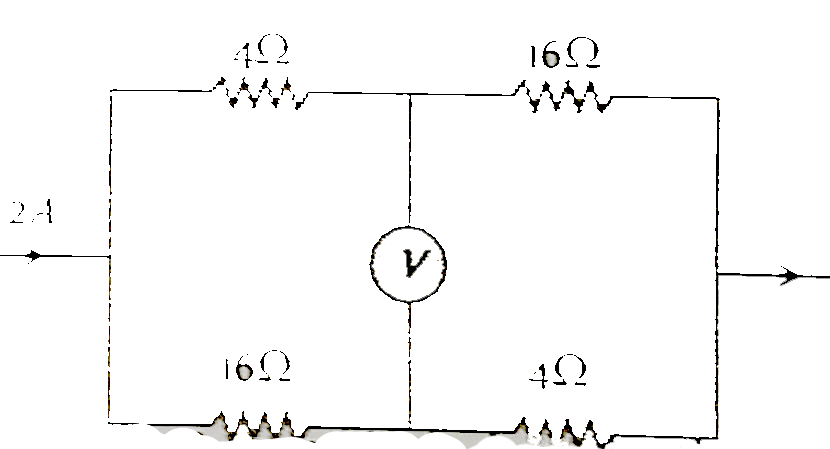
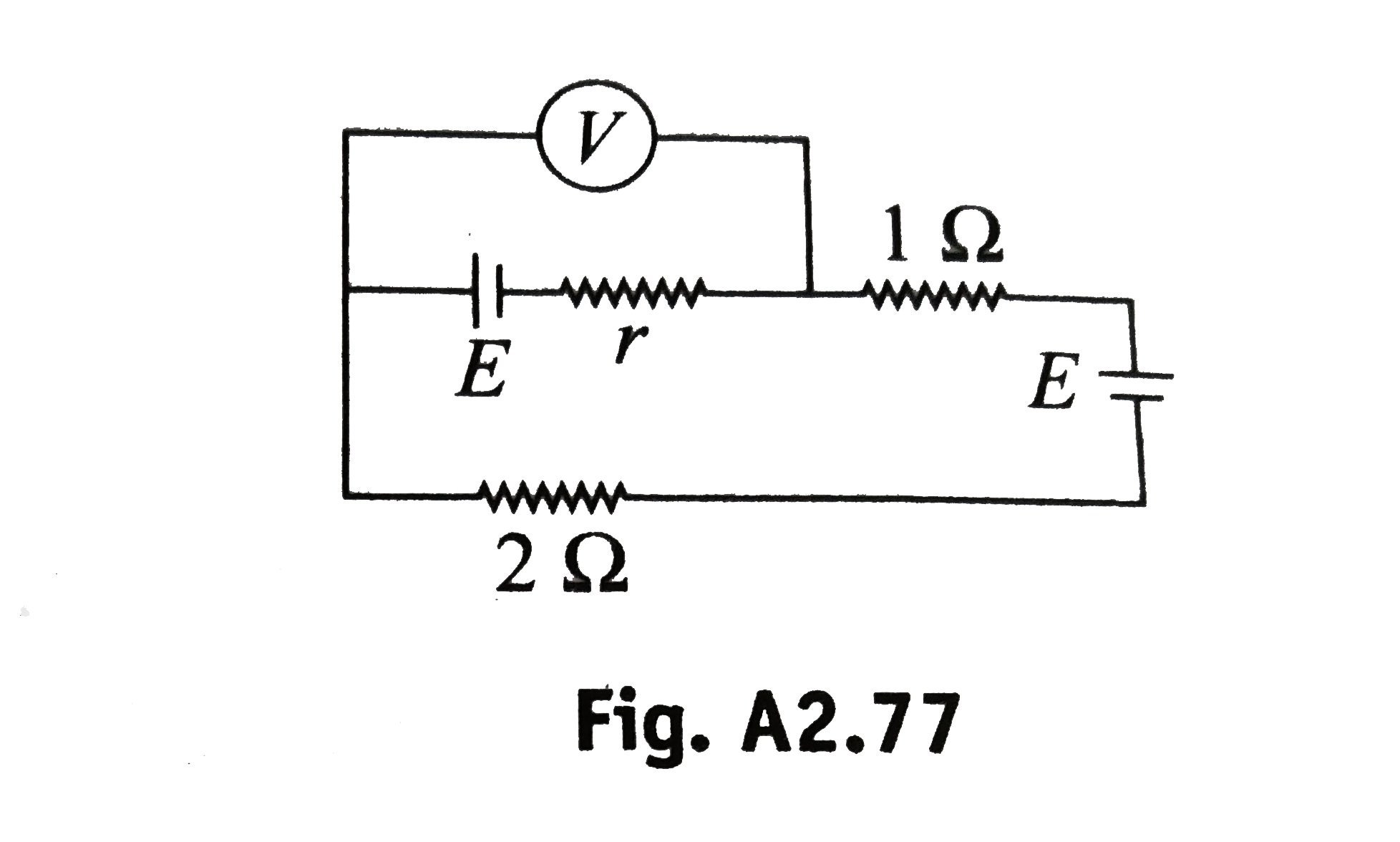
View SolutionIn the given circuit, the reading of ideal voltmeter is E/2. The internal resistance of the battery is
View SolutionIf LandR denote inductance and resistance , respectively , then the dimensions of L/R are
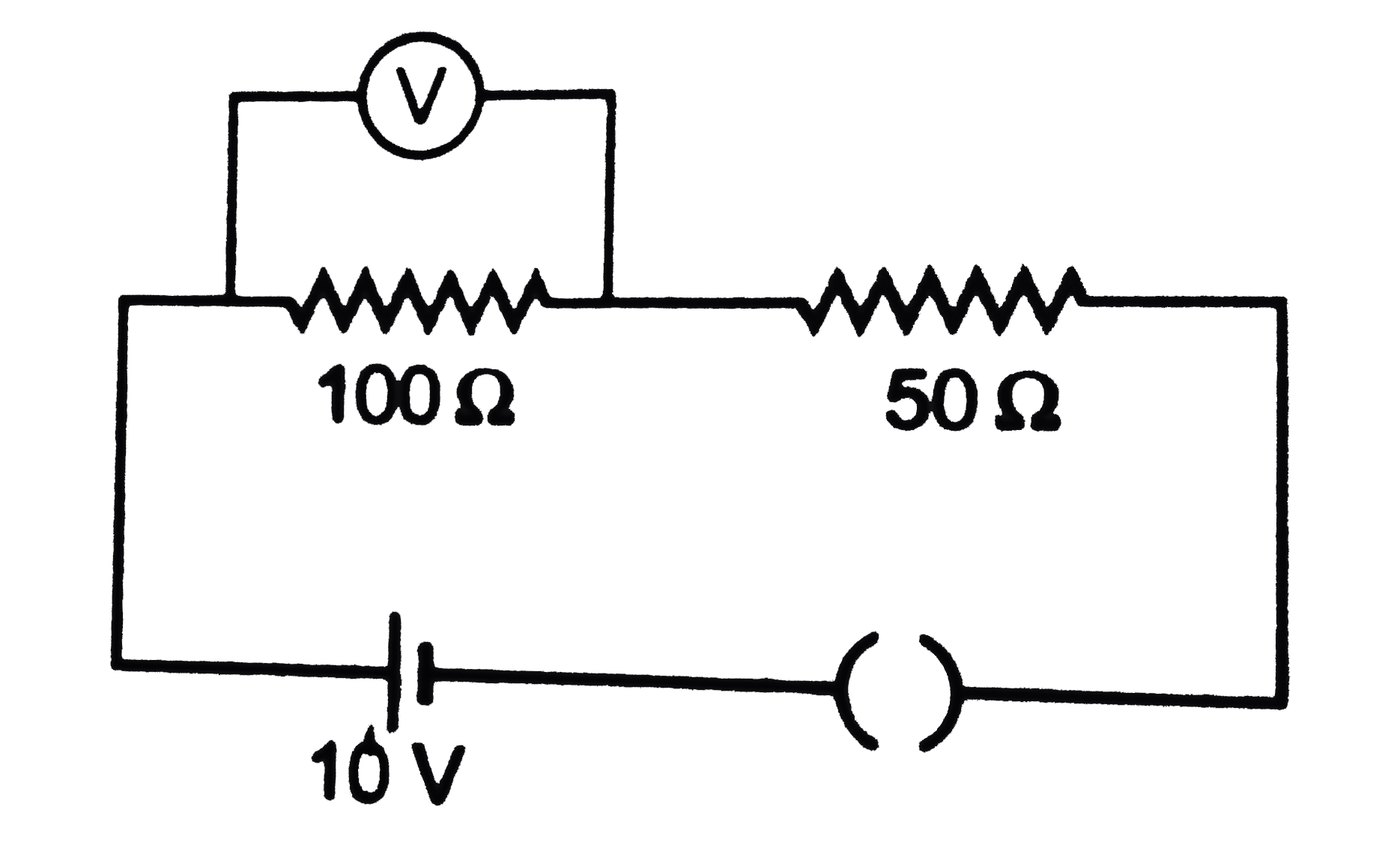
View SolutionIn the given circuit, the voltmeter records 5 volt. The resistance of the voltmeter in Ω is
View SolutionIn a series resonant circuit, the ac, voltage across resistance R, inductance L and capacitance are 5V, 10V and 10V, respectively. The ac. voltage applied to the circuit will be
View SolutionThe reading of ammeter and voltmeter in the given circuit is
_PHY_E06_306_Q01.png)
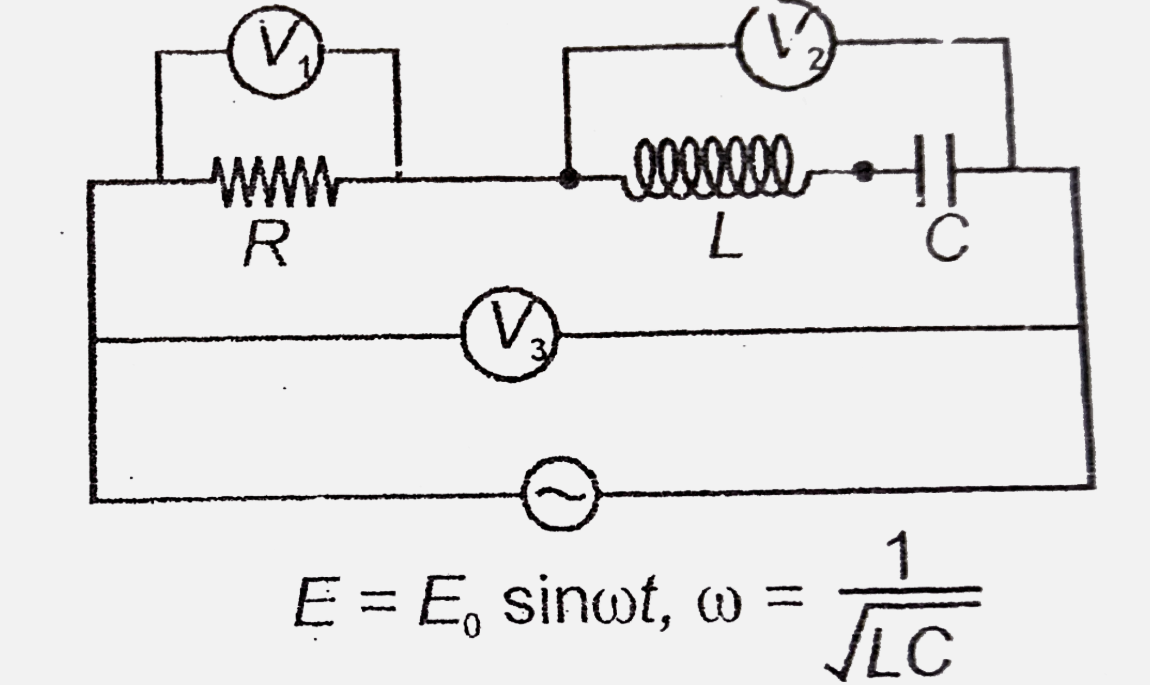
View SolutionIn the circuit shown, the readings of voltmeters V1,V2andV3 are given by
View SolutionIn the given circuit, the voltmeter records 5 V. The resistance of the voltmeter in Ω is

View SolutionIn the given circuit, Fig., the reading of voltmeter V1 and V2 300 votls each. The reading of the voltemeter V3 and ammeter A are respectively
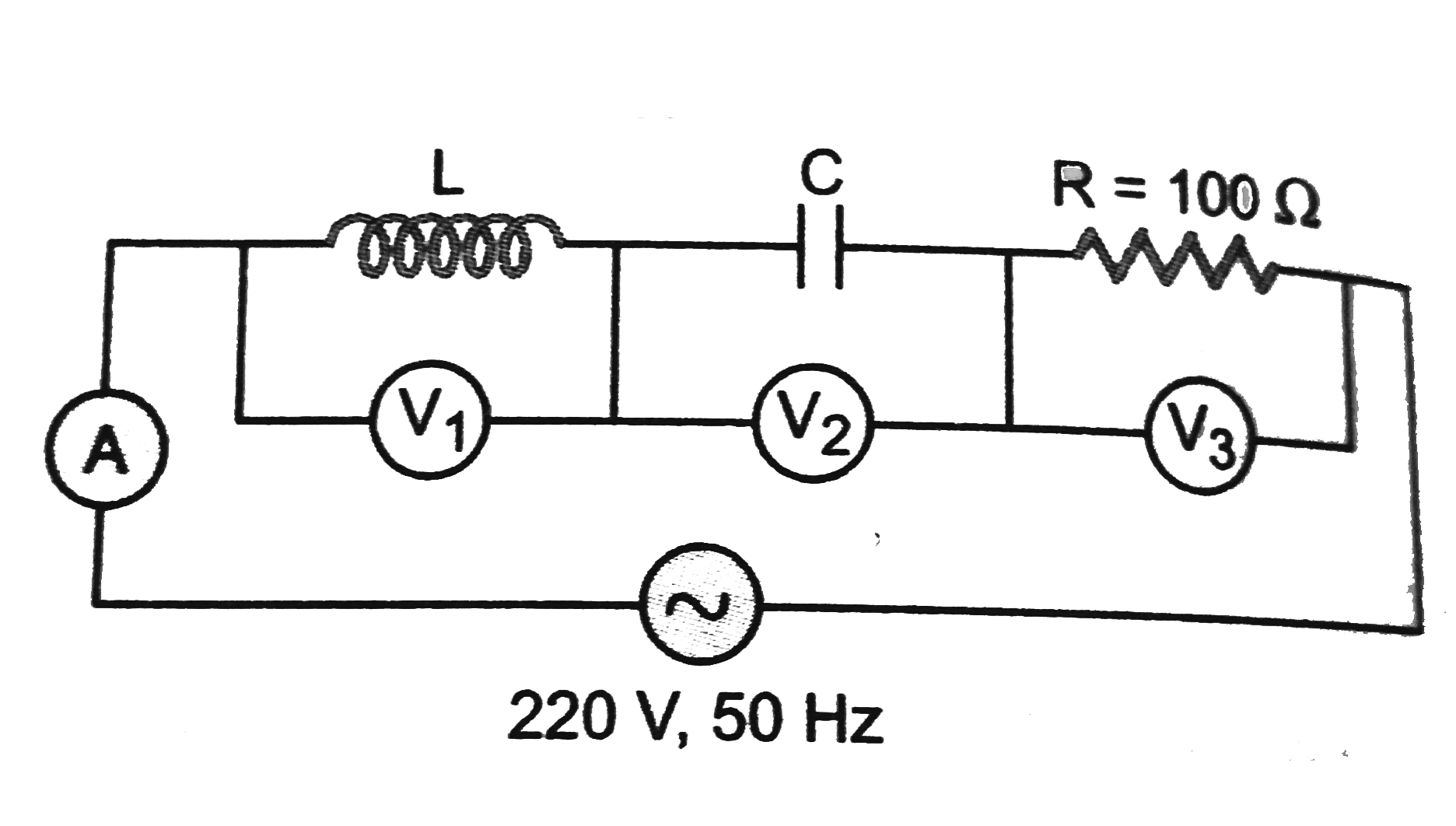
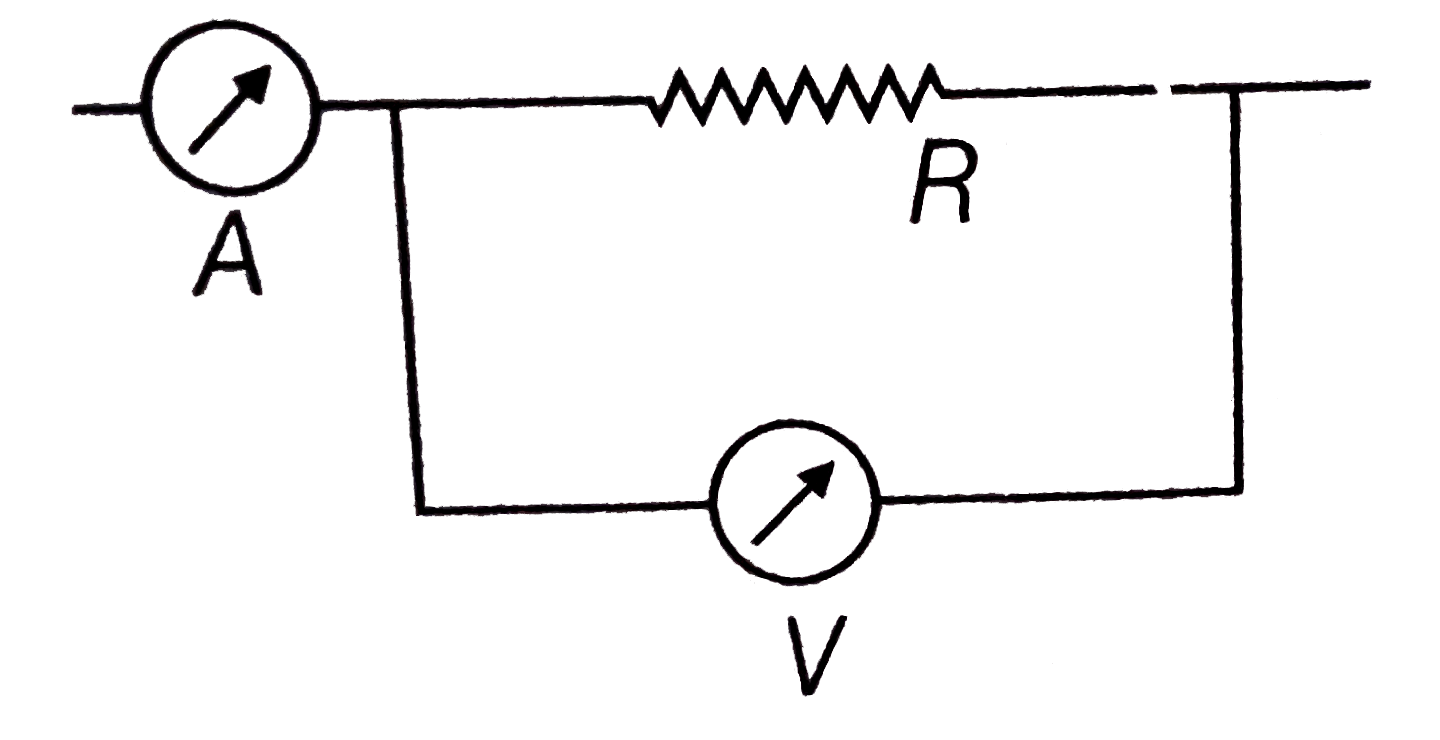
View SolutionIn the adjoining circuit diagram, the readings of ammeter and voltmeter are 2 A and 120 V, respectively. If the value of R is 75Ω, then the voltmeter resistance will be
View Solution