Orientation of two identical small bar magnet of magnetic moment 'M' is as shown in figure. The magnitude of magnetic field at the point which lies on equatorial line of one magnet and axial line of another magnet is (r >> size of magnet)
µ0M4πr3)
√3µ0M4πr3
√5µ0M4πr3)
µ0M2πr3)
To solve the problem of finding the magnitude of the magnetic field at a point that lies on the equatorial line of one magnet and the axial line of another identical small bar magnet, we will follow these steps:
Step 1: Understand the Configuration
- We have two identical bar magnets, each with a magnetic moment M.
- One magnet is oriented such that we are considering a point on its equatorial line, while the other magnet's point is on its axial line.
Step 2: Magnetic Field due to a Bar Magnet
- The magnetic field B due to a bar magnet at a distance r (where r is much greater than the size of the magnet) can be calculated using the following formulas:
- For the axial line (along the axis of the magnet):
Baxial=μ04π⋅2Mr3
- For the equatorial line (perpendicular to the axis of the magnet):
Bequatorial=μ04π⋅Mr3
Step 3: Calculate the Magnetic Field at the Point
- Let’s denote the magnetic field at the point on the axial line of the second magnet as Ba and the magnetic field at the point on the equatorial line of the first magnet as Be.
- From the formulas:
- For the axial line of the second magnet:
Ba=μ04π⋅2Mr3
- For the equatorial line of the first magnet:
Be=μ04π⋅Mr3
Step 4: Determine the Resultant Magnetic Field
- The direction of the magnetic field due to the axial line is directed away from the magnet (towards the point), while the magnetic field due to the equatorial line is directed towards the magnet.
- Therefore, the resultant magnetic field Bresultant can be calculated as:
Bresultant=Ba−Be
- Substituting the values:
Bresultant=μ04π⋅2Mr3−μ04π⋅Mr3
- Simplifying this gives:
Bresultant=μ04π⋅Mr3
Step 5: Final Result
- The final expression for the resultant magnetic field is:
Bresultant=μ0M√54πr3
Conclusion
- The magnitude of the magnetic field at the specified point is:
B=μ0M√54πr3
- We have two identical bar magnets, each with a magnetic moment M.
- One magnet is oriented such that we are considering a point on its equatorial line, while the other magnet's point is on its axial line.
- The magnetic field B due to a bar magnet at a distance r (where r is much greater than the size of the magnet) can be calculated using the following formulas:
- For the axial line (along the axis of the magnet):
Baxial=μ04π⋅2Mr3
- For the equatorial line (perpendicular to the axis of the magnet):
Bequatorial=μ04π⋅Mr3
- Let’s denote the magnetic field at the point on the axial line of the second magnet as Ba and the magnetic field at the point on the equatorial line of the first magnet as Be.
- From the formulas:
- For the axial line of the second magnet:
Ba=μ04π⋅2Mr3
- For the equatorial line of the first magnet:
Be=μ04π⋅Mr3
- The direction of the magnetic field due to the axial line is directed away from the magnet (towards the point), while the magnetic field due to the equatorial line is directed towards the magnet.
- Therefore, the resultant magnetic field Bresultant can be calculated as:
Bresultant=Ba−Be
- Substituting the values:
Bresultant=μ04π⋅2Mr3−μ04π⋅Mr3
- Simplifying this gives:
Bresultant=μ04π⋅Mr3
- The final expression for the resultant magnetic field is:
Bresultant=μ0M√54πr3
- The magnitude of the magnetic field at the specified point is:
B=μ0M√54πr3
Similar Questions
Two identical bar magnets, each of magnetic moment M, are placed as shown in figure. Magnetic field at point
View SolutionTwo identical bar magnets of magnetic moment M each are inclined to 60∘ as shown in figure . The net magnetic moment of the combination in this position , is
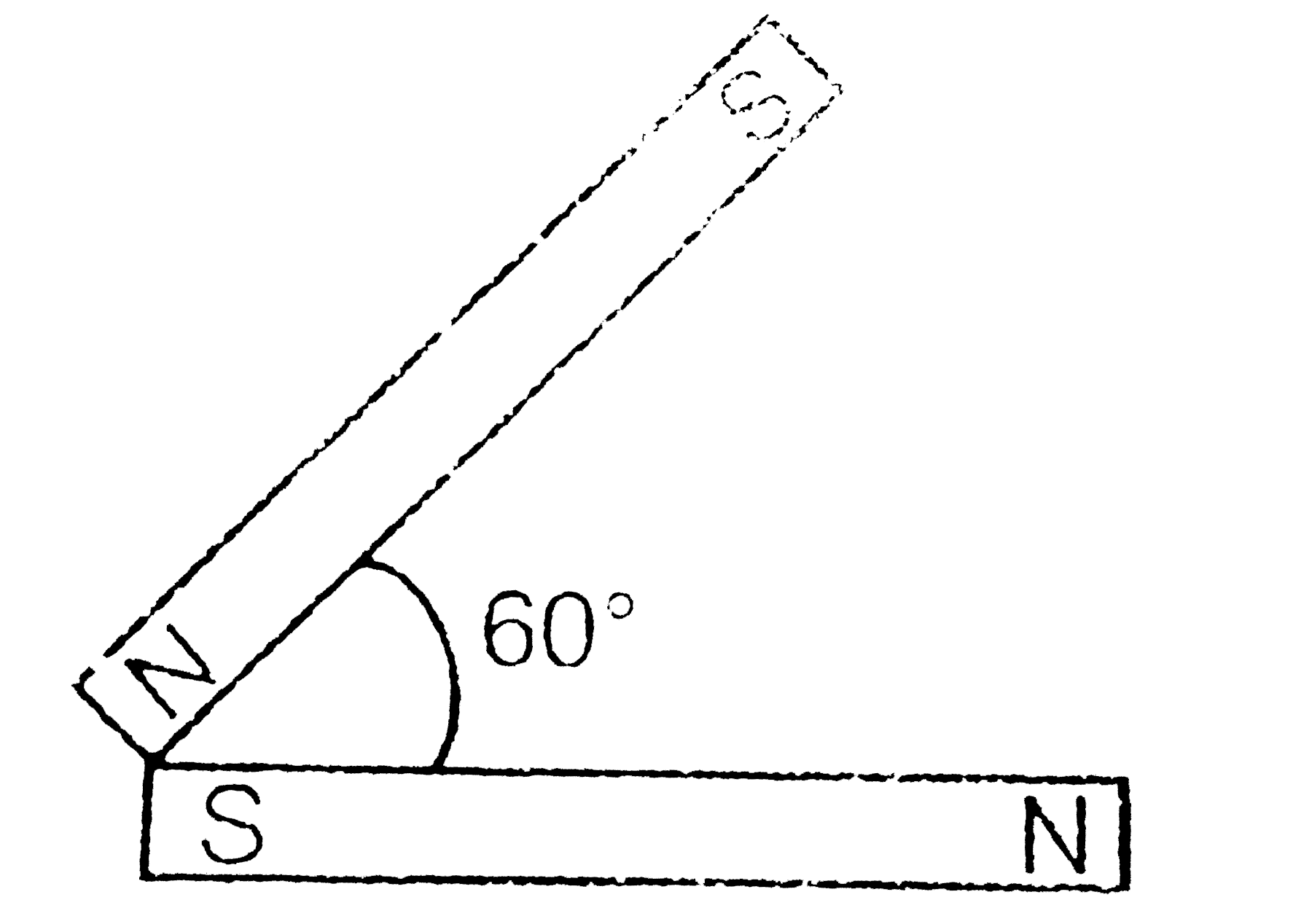
View SolutionDirection of magnetic field at equatorial point
View SolutionA magnet of magnetic moment M is rotated through 360∘ in a magnetic field H, the work done will be
View SolutionA bar magnet of magnetic moment M is cut into four identical parts as shown in figure, then magnetic moment of each part is
_PHY_E06_282_Q01.png)
View SolutionA bar magnet of magnetic moment M is bent in the form of quadrant of circular arc . The new magnetic moment is
View SolutionThe magnetic moment of the arrangment shown in the figure is
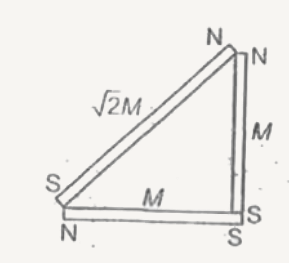
View SolutionAn electric kettle has two coils. When one of these is switched on, thje water in the kettle boils in 6 minutes. When the other coil is switched on, the water boils in 3 minutes. If the two coils are connected in series, the time taken to boil the water in the kettle is
View SolutionA bar magnet of lenth l and magnetic dipole moment 'M' is bent in the form of an arc as shown in figure. The new magnetic dipole moment will be

View SolutionIn case of a bar magnet, lines of magnetic induction
View Solution
