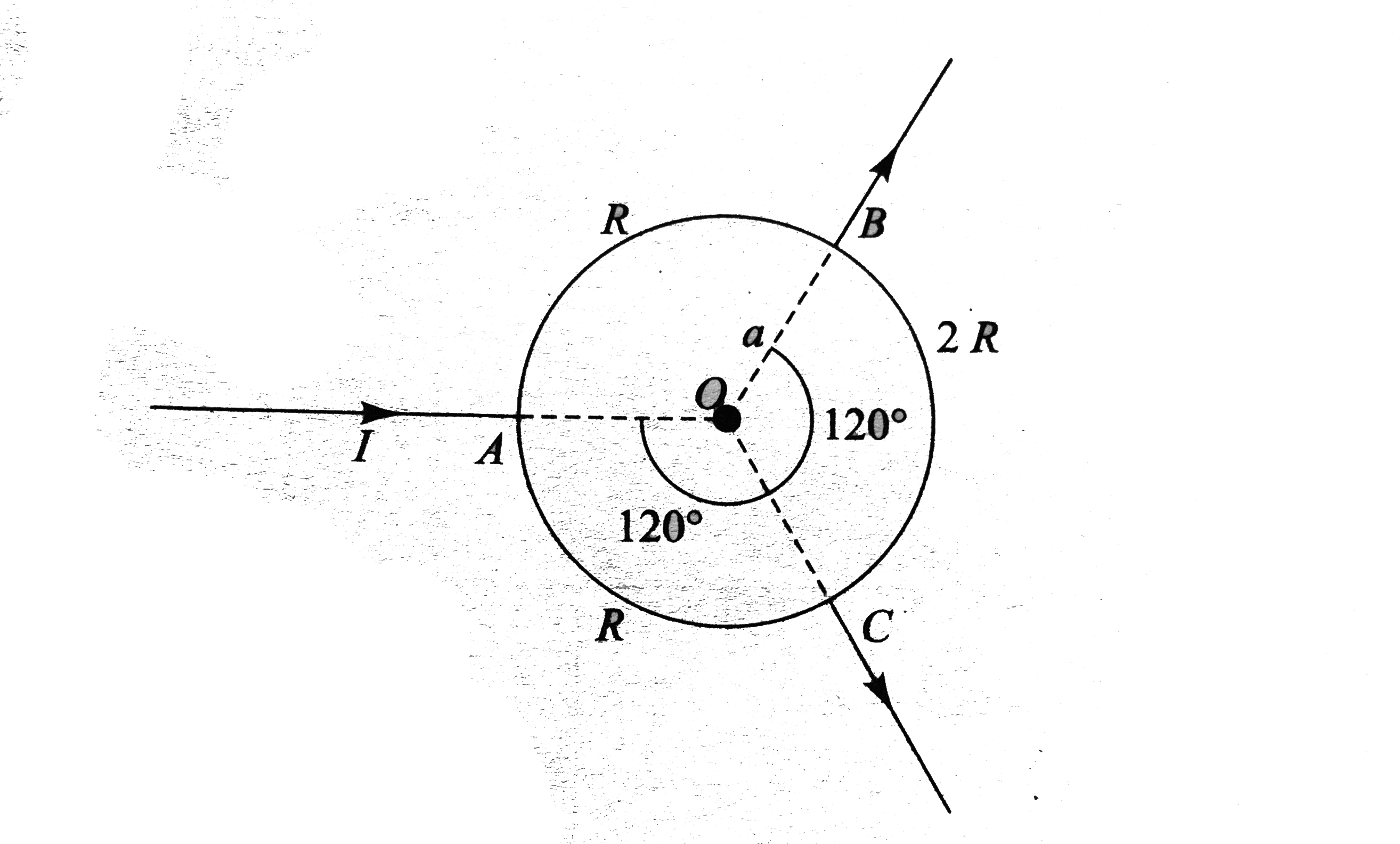
The resistance of three parts of a circular loop is shown in the figure. The magnetic field at the centre 0 is
Zero
[2μ0i5r]
[μ0i6r]
[μ0i3r]
To solve the problem of finding the magnetic field at the center O of a circular loop with three sections (A, B, and C) having different resistances, we can follow these steps:
1. Understanding the Configuration:
- We have a circular loop divided into three sections: A, B, and C.
- Each section is separated by 120 degrees.
- The current I flows through these sections.
Hint: Visualize the circular loop and the arrangement of the sections to understand how the current flows through each part.
2. Analyzing Current Flow:
- Since sections B and C are at the same potential (VB = VC), no current will flow through section BC.
- Therefore, the current flowing through section B (IB) and section C (IC) is zero: IB = IC = 0.
Hint: Remember that current flows from higher potential to lower potential. If two points are at the same potential, no current will flow between them.
3. Calculating Magnetic Field Contributions:
- The magnetic field produced by a current-carrying conductor at a point depends on the direction of the current and the distance from the conductor.
- The magnetic field at the center O due to section A (BA) and section C (BC) can be calculated using the Biot-Savart law or Ampere's law.
Hint: Recall that the magnetic field due to a circular loop at its center is given by the formula B = (μ₀ * I) / (4 * π * r) for a straight conductor, but here we need to consider the contributions from each section.
4. Direction of Magnetic Fields:
- The magnetic field due to section A will be in one direction, while the magnetic field due to section C will be in the opposite direction.
- Since IB = 0 and IC = 0, the contributions from B and C will cancel each other out.
Hint: Use the right-hand rule to determine the direction of the magnetic fields produced by each section.
5. Resultant Magnetic Field:
- Since the contributions from sections A and C cancel each other out and there is no contribution from section B, the resultant magnetic field at the center O is zero.
Hint: Consider the vector nature of magnetic fields; if two fields are equal in magnitude but opposite in direction, they cancel each other out.
6. Final Answer:
- The magnetic field at the center O is therefore 0.
Conclusion:
The magnetic field at the center O of the circular loop is 0.
- We have a circular loop divided into three sections: A, B, and C.
- Each section is separated by 120 degrees.
- The current I flows through these sections.
- Since sections B and C are at the same potential (VB = VC), no current will flow through section BC.
- Therefore, the current flowing through section B (IB) and section C (IC) is zero: IB = IC = 0.
- The magnetic field produced by a current-carrying conductor at a point depends on the direction of the current and the distance from the conductor.
- The magnetic field at the center O due to section A (BA) and section C (BC) can be calculated using the Biot-Savart law or Ampere's law.
- The magnetic field due to section A will be in one direction, while the magnetic field due to section C will be in the opposite direction.
- Since IB = 0 and IC = 0, the contributions from B and C will cancel each other out.
- Since the contributions from sections A and C cancel each other out and there is no contribution from section B, the resultant magnetic field at the center O is zero.
- The magnetic field at the center O is therefore 0.
The magnetic field at the center O of the circular loop is 0.
Topper's Solved these Questions
Similar Questions
The resistances of three parts of a circular loop are as shown in Fig. The magnetic field at the centre O is (current enters at A and leaves at B and C as shown)
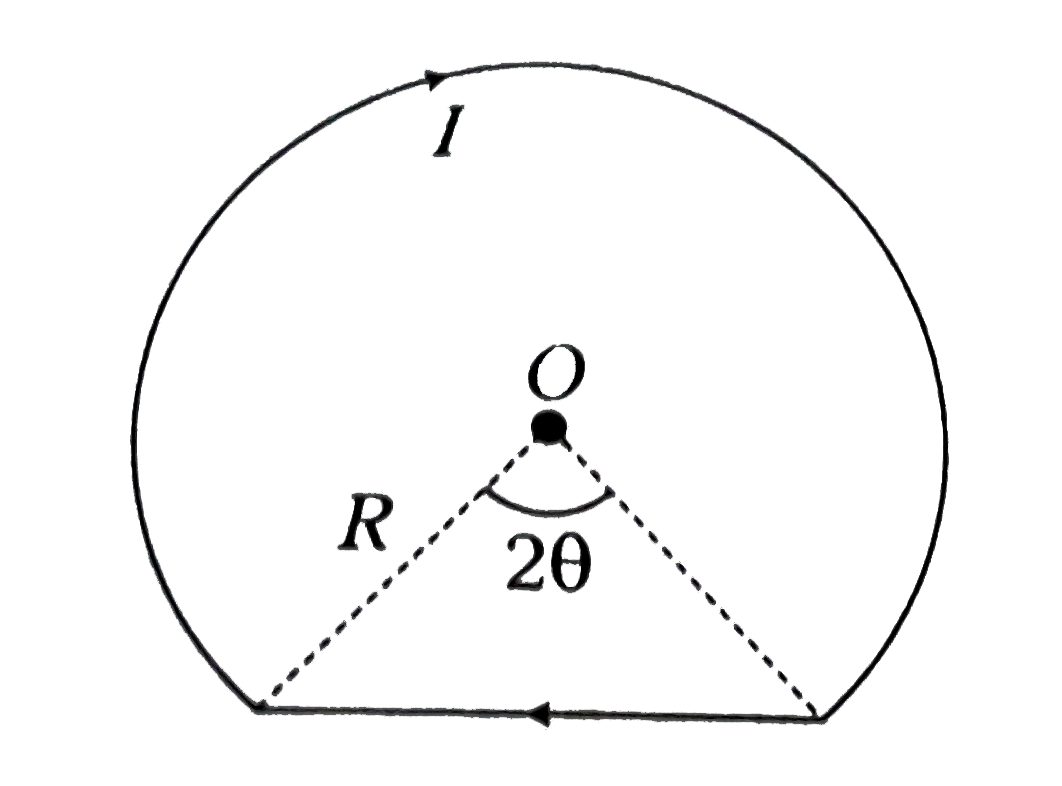
View SolutionA current l flows through a closed loop as shown in figure .The magnetic field at the centre O is
View SolutionA loop in the shape of an equilateral triangle triangle of side a carries a current I as shown in the figure.Find out the magnetic field at the centre C of the triangle.
View SolutionA current I is flowing thorugh the loop. The direction of the current and the shpae of the loop are as the shown in the figure. The magnetic fild at the centre of the loop is μ0IR times
(MA=R,MB=2R,∠DMA=90∘)
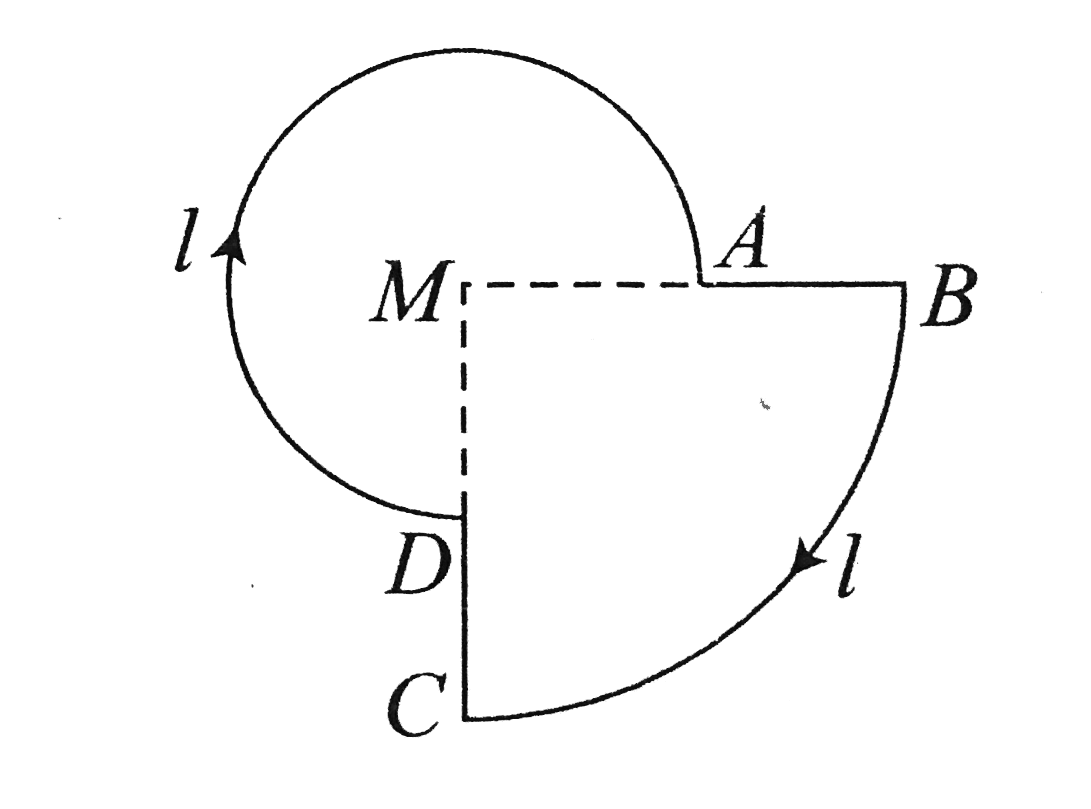
View SolutionA current I is flowing through the loop , as shown in the figure . The magnetic field at centre O is
View SolutionA long wire carries a steady curent . It is bent into a circle of one turn and the magnetic field at the centre of the coil is B. It is then bent into a circular loop of n turns. The magnetic field at the centre of the coil will be
View SolutionA long wire carries a steady curent . It is bent into a circle of one turn and the magnetic field at the centre of the coil is B. It is then bent into a circular loop of n turns. The magnetic field at the centre of the coil will be
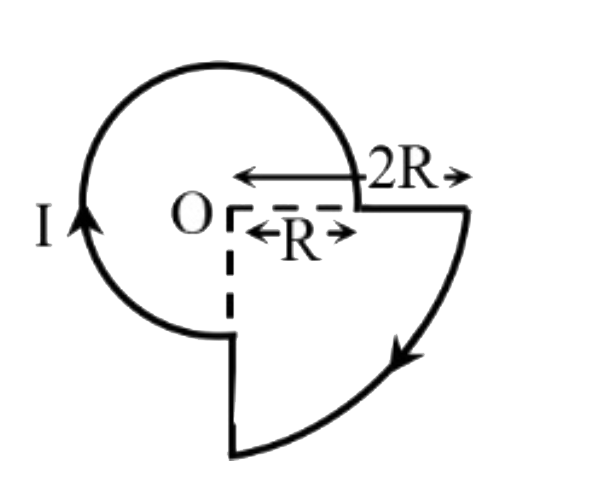
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is

View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is :

View SolutionA long wire carrying a steady current is bent into a circular loop of one turn. The magnetic field at the centre of the loop is B. it is then bent into a circular coil of n turns. The magnetic field at the centre of this coil of n turns will be
View Solution
