If the instantaneous charge on the capacitor is (100mμC) and current through the circuit is decreasing at the rate (2×310) A/s then potential diffference (VA−VB) is equal to
(−)3 V
3 V
27 V
7 V
To find the potential difference VA−VB across the capacitor in the given circuit, we can use the relationship between charge, current, and potential difference. Here is a step-by-step solution:
Step 1: Identify the given values
- Instantaneous charge on the capacitor, Q=100μC=100×10−6C
- Rate of change of current, dIdt=−2×103A/s (the negative sign indicates that the current is decreasing)
Step 2: Use the relationship between current, charge, and capacitance
The current I through a capacitor is related to the charge Q by the equation:
I=dQdt
From this, we can express the change in charge with respect to time as:
dQdt=CdVdt
where C is the capacitance and V is the potential difference across the capacitor.
Step 3: Calculate the capacitance
Assuming we have a capacitance value C (not given in the question), we can proceed with the calculations. However, since we need to find VA−VB, we can use the formula directly.
Step 4: Calculate the potential difference using the given values
Using the formula for potential difference across the capacitor:
VA−VB=QC+IR+Vs+LdIdt
Where:
- I is the current through the circuit (assumed to be 1 A)
- R is the resistance (assumed to be 2 ohms)
- Vs is the supply voltage (assumed to be 5 V)
- L is the inductance (assumed to be 10 mH)
Step 5: Substitute the values into the equation
Substituting the values into the equation:
VA−VB=100×10−610×10−6+(1×2)+5+(10×10−3)×(−2×103)
Calculating each term:
1. 100×10−610×10−6=10V
2. 1×2=2V
3. 5V
4. (10×10−3)×(−2×103)=−20V
Step 6: Combine all the terms
Now, combine all the terms:
VA−VB=10+2+5−20=−3V
Final Result
The potential difference VA−VB is equal to −3V.
- Instantaneous charge on the capacitor, Q=100μC=100×10−6C
- Rate of change of current, dIdt=−2×103A/s (the negative sign indicates that the current is decreasing)
The current I through a capacitor is related to the charge Q by the equation:
I=dQdt
From this, we can express the change in charge with respect to time as:
dQdt=CdVdt
where C is the capacitance and V is the potential difference across the capacitor.
Assuming we have a capacitance value C (not given in the question), we can proceed with the calculations. However, since we need to find VA−VB, we can use the formula directly.
Using the formula for potential difference across the capacitor:
VA−VB=QC+IR+Vs+LdIdt
Where:
- I is the current through the circuit (assumed to be 1 A)
- R is the resistance (assumed to be 2 ohms)
- Vs is the supply voltage (assumed to be 5 V)
- L is the inductance (assumed to be 10 mH)
Substituting the values into the equation:
VA−VB=100×10−610×10−6+(1×2)+5+(10×10−3)×(−2×103)
Calculating each term:
1. 100×10−610×10−6=10V
2. 1×2=2V
3. 5V
4. (10×10−3)×(−2×103)=−20V
Now, combine all the terms:
VA−VB=10+2+5−20=−3V
The potential difference VA−VB is equal to −3V.
Similar Questions
If the instantaneous change on the capacitor is 100μC and current through the circuit is decreasing at the rate of 2×103 As then potential difference VA−VB is equal to
_PHY_E06_046_Q01.png)
View SolutionWhen the current in a certain inductor coil is 5.0A and is increasing at the rate of 10.0A/s,the magnitude of potential difference across the coil is 140V.When the current is 5.0A and decreasing at the rate of 10.0A/s,the potential difference is 60V.The self inductance of the coil is :
View SolutionIn the given circuit, current I is 2A and it is decreasing at the rate of 103AS−1.Then VB−VA is
_PHY_E06_148_Q01.png)
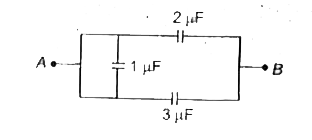
View SolutionIn the given circuit the charge on the plates of 1 μF capacitor, when 100 V battery is connected to the terminals A and B will be
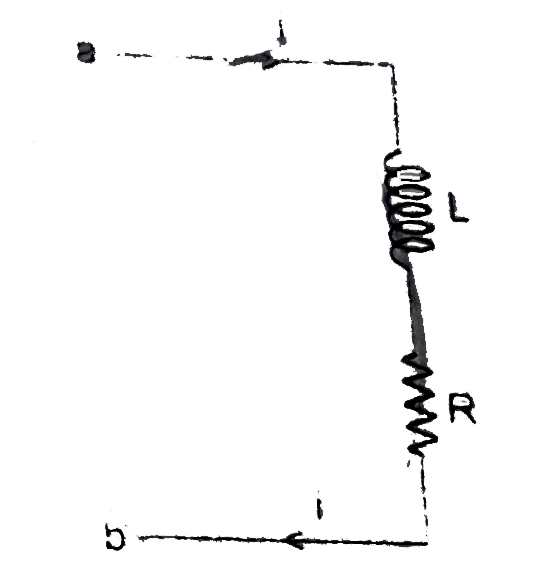
View SolutionWhen the current in the portion of the circuit shown in the figure is 2A and increasing at the rate of 1A/s,the measured potential difference Va−Vb=8V.However when the current is 2A and decreasing at the rate of 1A/s, the measured potential difference Va−Vb=4V.The values of R and L are:
View SolutionThe 500μF capacitor is charged at a steady rate of 100μC/s. The potential difference across the capacitor will be 10 V after an interval of
View SolutionThe 500μF capacitor is charged at a steady rate of 100μC/s. The potential difference across the capacitor will be 10 V after an interval of
View SolutionFigure shows part of a circuit. If l = 5A and is decreasing at a constant rate of 103A/s then VB−VA is
View SolutionAn ideal capacitor of capacitance 0.2μF is charged to a potential difference of 10V. The charging battery is than disconnected. The capacitor is then connected to an ideal inductor of self inductance 0.5mH. The current at a time when the potential difference across the capacitor is 5V is :
View SolutionTwo capacitors of capacitance 2μF and 3μF respectively are charged to potential difference 20 V and 40 V respectively. Now the capacitors are connected in series with a resistance such that the positively charged plate of one capacitor is connected to the positively charged plate of the other. The initial current through the resistance is I0. The potential difference across the 2μF capacitor at the instant the current has reduced to I02 is_______ V.
View Solution
